TransE - 简单但有效的知识图谱表示学习方法

介绍

来自论文 NIPS 2013年的 Translating Embeddings for Modeling Multi-relational Data。

这个方法开创了KGE中的一种思考方式，虽然简单，但是值得一读，因为有时候越简单的方法，取得的效果可能没有人们想得那么差。

针对的问题

The problem of embedding entities and relationships of multirelational data in low-dimensional vector spaces.

针对的研究对象

Multi-relational data refers to directed graphs whose nodes correspond to entities and edges of the form (head, label, tail) , denoted $(h, l, t)$ , each of which indicates that there exists a relationship of name label between the entities head and tail.

之前研究存在问题

• 表达能力上升以计算成本上升为代价

The greater expressivity of these models comes at the expense of substantial increases in model complexity which results in modeling assumptions that are hard to interpret, and in higher computational costs.

• 正则化方法难以设计导致过拟合

such approaches are potentially subject to either overfitting since proper regularization of such high-capacity models is hard to design,

• 非凸优化导致欠拟合

or underfitting due to the non-convex optimization problems with many local minima that need to be solved to train them.

研究目标

模型希望达到的目标：

• easy to train,
• contains a reduced number of parameters,
• and can scale up to very large databases

in complex and heterogeneous multi-relational domains simple yet appropriate modeling assumptions can lead to better trade-offs between accuracy and scalability.

想法

Relationships are represented as translations in the embedding space: if $(h, l, t)$ holds, then the embedding of the tail entity $t$ should be close to the embedding of the head entity $h$ plus some vector that depends on the relationship $l$ .

模型的基本想法是head的向量表示 $h$ 与relation的向量表示 $r$ 之和与tail的向量表示 $t$ 越接近越好，即：

$$
h+r \approx t
$$

这里的“接近”可以使用L1或L2范数进行衡量，这也是一个可以调节的超参数。

方法过程

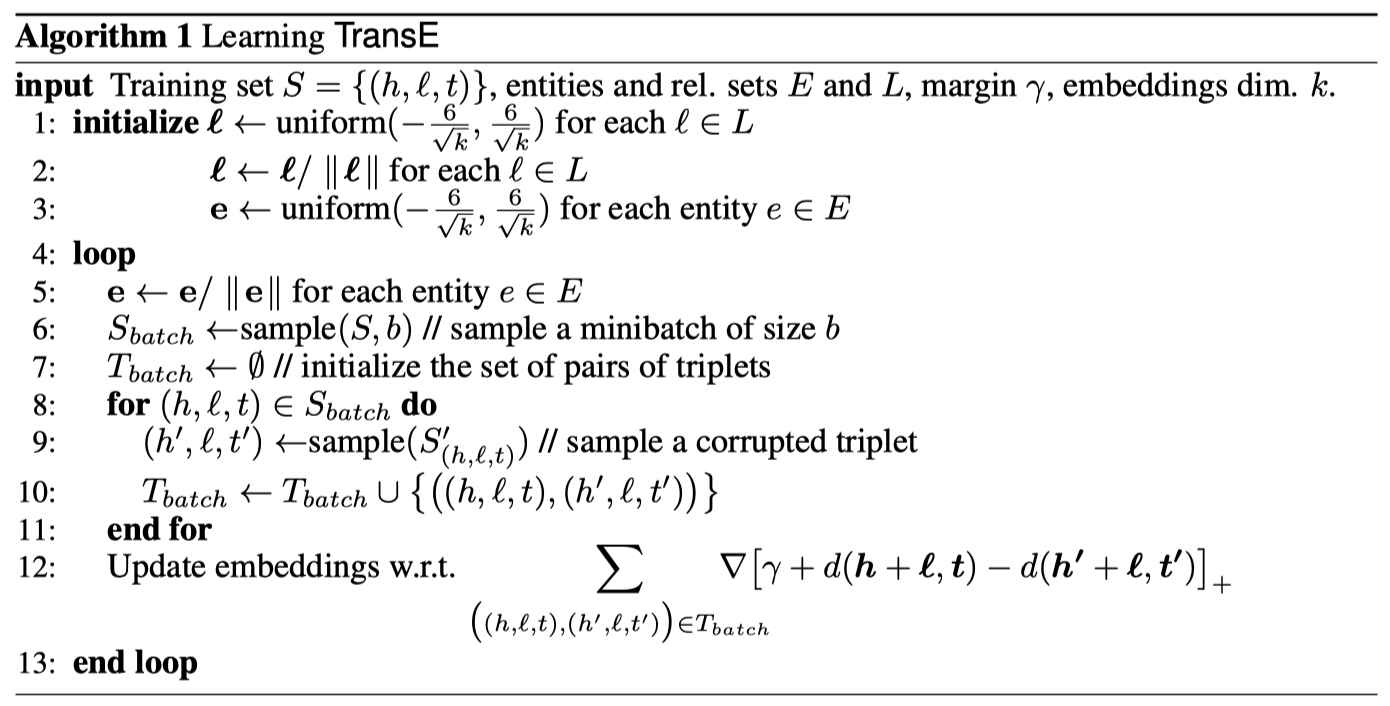
损失函数

损失函数是使用了负抽样的max-margin函数（原文为：a margin-based ranking criterion）。

$$
L(y, y^{\prime}) = \max(0, margin - y + y^{\prime})
$$

• $y$ 是正样本的得分；
• $y^{\prime}$ 是负样本的得分。

然后使损失函数值最小化，当这两个分数之间的差距大于margin的时候就可以了(我们会设置这个值，通常是1，这个是超参数)。

由于我们使用距离来表示得分，所以我们在公式中加上一个减号，知识表示的损失函数为：

$$
L(h,r,t) = \max(0, d_{pos} - d_{neg} + margin)
$$

其中，$d$ 是：

$$
d = \Vert h+r -t \Vert
$$

这是L1或L2范数。至于如何得到负样本，则是将head实体或tail实体替换为三元组中的随机实体，具体的方法可以参考 知识图谱表示学习：训练方法。

需要调节的参数

对于模型本身来说，只需要确定：

• 实体和关系的维度：embedding size
• 衡量接近程度的指标：L1或者L2
• margin

即可。

评估

使用的数据集

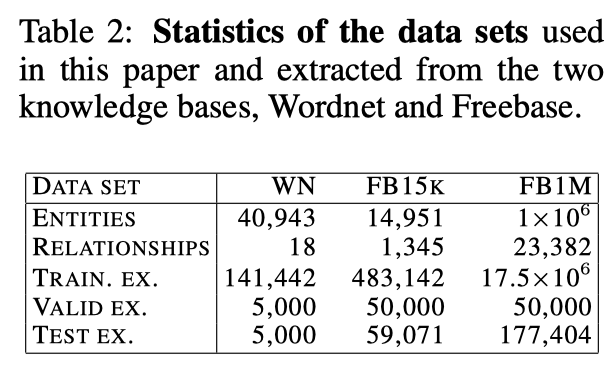
实验设计

• 评估指标

  • mean rank
  • hits@10

• 过滤真实三元组

这部分可以参考 知识图谱表示学习：评估方法。

评估结果

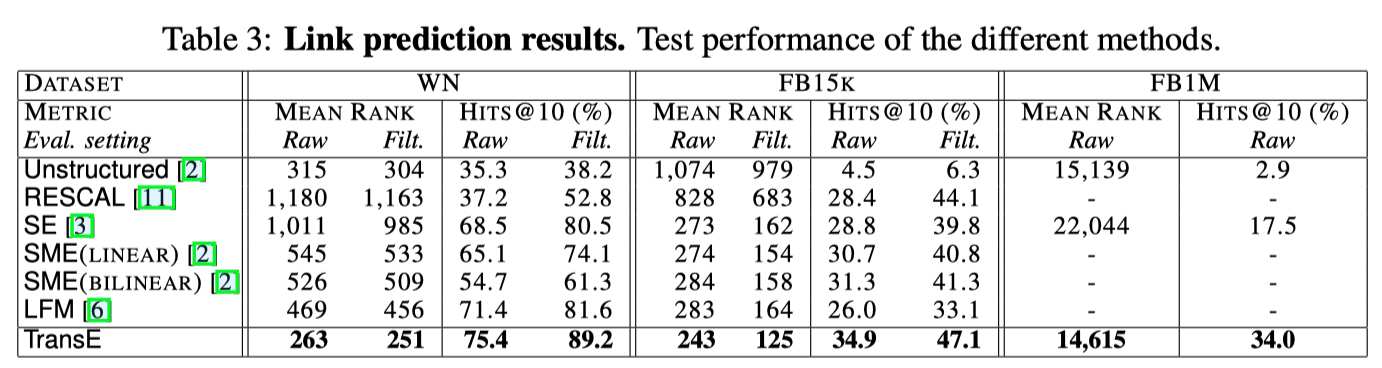
参数设置

• optimizer: stochastic gradient descent
• lr: 0.001, 0.01, 0.1
• margin: 1, 2, 10
• dimension k: 20, 50
• regularization: L1, L2
• epochs: <1000

缺陷

• simplicity
• 只适合处理一对一的关系，不适合一对多/多对一/多对多的关系。

  举个例子，有两个三元组（中国科学院大学，地点，北京）和（颐和园，地点，北京），使用TransE进行表示的话会得到中国科学院大学的表示向量和颐和园的表示向量很接近，甚至完全相同。但是它们的亲密度实际上可能没有这么大。

总结

这个方法从模型角度来看，很简单，但是要注意文章的目标是，取得预测性能和计算性能之间的平衡，也就说是比我强的没我快，比我快的没我强。

而且整个模型，很优美，没有任何繁琐的东西，是值得读的一篇入门的文章。