文章来源: RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space
之前研究中的问题
不能对三种关系同时进行建模和推理。
None of existing models is capable of modeling and inferring all the above patterns: symmetry/antisymmetry, inversion, and composition。
例子说明
- symmetry:婚姻,双向关系;
- antisymmetry:孝顺,单向关系;
- inversion:上位词和下位词,正向和反向关系;
- composition:我母亲的丈夫是我父亲,关系组合计算;
想法
Motivation is from Euler’s identity: a unitary complex number can be regarded as a rotation in the complex plane.
$$
e^{i\theta} = \text{cos}\theta + i\text{sin}\theta
$$
即,任何一个复数都可以看作复平面上的一个旋转向量。
RotatE model maps the entities and relations to the complex vector space and defines each relation as a rotation from the source entity to the target entity.
形式化表达:
Given a triplet $(h, r, t)$ , we expect that $t = h \circ r$ , where $h, r, t \in \mathbb{C}^k $ are the embeddings, the modulus $| r_i | = 1$ and $\circ$ denotes the Hadamard (element-wise) product. Specifically, for each dimension in the complex space, we expect that:
$$
t_i = h_i r_i , \text{where} \ h_i , r_i , t_i \in \mathbb{C}^k \text{and} \ | r_i | = 1.
$$
说明:
symmetrica relation $r$ is symmetric if and only if each element of its embedding $r_i$ , satisfies $r_i= e^{0/i\pi}= \pm1$ ;
inverseTwo relations $r_1$ and $r_2$ are inverse if and only if their embeddings are
conjugates: $r_2= \overline{r}_1$ ;compositiona relation $r_3= e^{i\theta_3} $ is a combination of other two relations $r_1= e^{i\theta_1}$ and $r_2= e^{i\theta_2}$ if and only if $r_3 = r_1 \circ r_2$ (i.e. $\theta_3 = \theta_1 + \theta_2$ ).
方法说明
Relations Formal definition
Definition 1. A relation $r$ is symmetric (antisymmetric) if $\forall x, y$
$$ r(x, y) ⇒ r(y, x) \ ( r(x, y) ⇒ ¬r(y, x) ) $$
A clause with such form is a symmetry (antisymmetry) pattern.
Definition 2. Relation $r_1$ is inverse to relation $r_2$ if $\forall x, y$
$$r_2 (x, y) ⇒ r_1(y, x)$$
A clause with such form is a inversion pattern.
Definition 3. Relation $r_1$ is composed of relation $r_2$ and relation $r_3$ . if $\forall x, y, z$
$$r_2 (x, y) ∧ r_3 (y, z) ⇒ r_1 (x, z)$$
A clause with such form is a composition pattern.
建模思考过程
我们希望达成以下目标:
- (非)对称关系
$$ r(x, y) ⇒ r(y, x) \ ( r(x, y) ⇒ ¬r(y, x))$$ - 逆向关系
$$r_2 (x, y) ⇒ r_1(y, x)$$ - 组合关系
$$r_2 (x, y) ∧ r_3 (y, z) ⇒ r_1 (x, z)$$
那就要找到一个函数能够实现这三种关系的表示。
TransE能够对这三种关系同时建模吗?稍稍分析一下:
对于
symmetric需要找到满足条件的关系的embeddings
$$ r(x, y) ⇒ r(y, x)$$
$$x + r_i = y$$
$$y + r_j = x$$
$$r_i = r_j$$
则,只能 $r_i = r_j = 0$ ,所以不能表示
symmetric。
对于
antisymmetry$$ r(x, y) ⇒ ¬r(y, x) $$
要求:
$$x + r_i = y$$
$$y + r_j = x$$
$$r_i \ne r_j$$
模型是能够满足要求的,只要保证:
$$r_i + r_j = 0$$
$$r_i \ne r_j$$
至于建模的效果好不好,那是另外一回事。
对于
inversion需要满足:
$$r_2 (x, y) ⇒ r_1(y, x)$$
从上述反对称的角度进一步看,在满足反对称的同时,它也就满足了
inversion关系的表达。$$x + r_2 = y$$
$$y + r_1 = x$$
$$r_i \ne r_j$$
只要满足以下条件就行:
$$r_1 = - r_2$$对于
composition需要满足:
$$r_2 (x, y) ∧ r_3 (y, z) ⇒ r_1 (x, z)$$
对于使用TransE来表示如下:
$$x + r_2 = y$$
$$y + r_3 = z$$
$$x + r_1 = z$$
对
TransE的表示进行变形:$$x + r_2 + r_3 = x + r_1$$
自然得到:
$$r_2 + r_3 = r_1$$
总结来看,TransE除了对称关系无法表达,其余关系均能表达,现在的问题是如何在TransE的基础上对对称关系建模,使得关系的embedding不全为0.
那么要明白的是TransE为啥不能建模对称关系?因为在使用平移建模关系时,对应的是加法运算。那么换一种想法,加法不行,那么乘法是不是可以?
为了满足对称关系的要求,有如下的关系:
$$hr_i = t$$
$$tr_j = h$$
$$r_i = r_j$$
能够推导出以下关系:
$$tr_jr_i = t$$
$$r_jr_i = 1$$
$$r_ir_i = 1 = r_jr_j$$
上述可以看成是一个维度上的情况,当换到所有embedding上的维度时,这就自然引出了 Hadmard (or element-wise) product。
这就是当时使用Hadmard (or element-wise) product需要满足的条件,为了建模对称关系,要保证:
$$r_ir_i = 1 = r_jr_j$$
其实,这就是上文中要保证
$$| r_i | = 1$$
的原因。
We map the head and tail entities $h$ , $t$ to the complex embeddings, i.e., $\mathbf{h}, \mathbf{t} \in \mathbb{C}^ k$ , then we define the functional mapping induced by each relation $\mathbf{r}$ as an element-wise rotation from the head entity $\mathbf{h}$ to the tail entity $\mathbf{t}$ .
这里,开始时不明白为什么选择 Hadmard (or element-wise) product,这个与欧拉公式是啥关系?因为原文用了 define,我觉得逻辑可能并不充分,可能是一种启发式的选择,只要它满足三种关系的形式化建模就行。
其实这种思考方法,我仔细想了一下,其实是两种方式的区别,我一开始不明白,是因为没有严格的逻辑推导出要用Hadmard,所以它出来时,我一头雾水,这是一种从因到果的思考方式。但是这里换一种方法去思考,Hadmard的结果满足我们开始时的假设,即能够建模对称关系,因此我们选了它,这是一种由果及因的方式,我的感觉,在ML领域这种方式好像更常见,也是被数学系的人吐槽的原因。
用Hadmard product验证关系约束
验证三种关系如下:
对于
symmetric需要找到满足条件的关系的embeddings
$$ r(x, y) ⇒ r(y, x)$$
$$\mathbf{h} \circ \mathbf{r_i} = \mathbf{t}$$
$$\mathbf{t} \circ \mathbf{r_j} = \mathbf{h} $$
$$\mathbf{r_i} = \mathbf{r_j} $$
推导出:
$$\mathbf{r_i} \circ \mathbf{r_i} = 1 = \mathbf{r_j} \circ \mathbf{r_j} $$
符合。对于
antisymmetry类似的,
$$ r(x, y) ⇒ ¬r(y, x) $$推导出,
$$\mathbf{r_i} \circ \mathbf{r_i} \ne 1 $$
符合。对于
inversion需要满足:
$$r_2 (x, y) ⇒ r_1(y, x)$$
$$\mathbf{h} \circ \mathbf{r_i} = \mathbf{t}$$
$$\mathbf{t} \circ \mathbf{r_j} = \mathbf{h} $$
推导出:
$$\mathbf{r_i} \circ \mathbf{r_j} = 1 $$$$\mathbf{r_i} = \mathbf{r_j}^{-1} $$
符合。
对于
composition需要满足:
$$r_2 (x, y) ∧ r_3 (y, z) ⇒ r_1 (x, z)$$
根据:
$$\mathbf{x} \circ \mathbf{r_2} = \mathbf{y}$$
$$\mathbf{y} \circ \mathbf{r_3} = \mathbf{z} $$
$$\mathbf{x} \circ \mathbf{r_1} = \mathbf{z} $$
推导出:
$$\mathbf{x} \circ \mathbf{r_2} \circ \mathbf{r_3} = \mathbf{x} \circ \mathbf{r_1} $$$$\mathbf{r_2} \circ \mathbf{r_3} = \mathbf{r_1}$$
完美得出。
总结来看,Hadmard product能够完美建模三种关系,到此,我们的假设成立。
与欧拉公式的关系
用类比的方法来看,TransE是将所有的实体和关系映射到embedding space中,也就是实平面,使用的是向量加法运算,三者之间的关系可以使用平移这种操作来建立关联。
那么Hadmard product实现的是向量元素乘法运算,如果放到实平面中,这没办法对应一个操作,不管是用矩阵乘法实现的线性变换,还是加上平移的仿射变换,都没办法对应将两个同样长度的向量经过元素相乘得到同样长度的向量,因此在理论上说不过去。
那么,换到复平面上,会怎么样?
我们知道复平面上一个复数的表示方法有好几种:
- 代数:$a+ib$,以 $(1,i)$ 为基的线性组合;
- 指数形式
- 极坐标
- 向量形式
- 矩阵乘法
具体的内容可以参看这里。
通过欧拉公式可以将指数形式和极坐标建立关系。
此时,复数的相乘可以看做矩阵变换:
$$z_1z_2 =(a+ib)(c+id) = (ac-bd)+(bc+ad)i$$
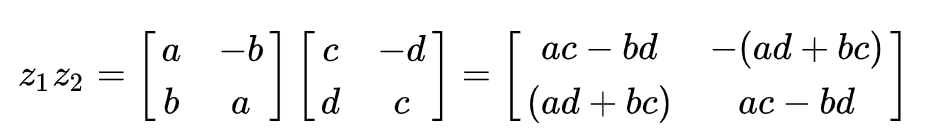
我们只要把embedding拆成实部和虚部,然后再利用复数的乘法进行计算,就同样能得到实部和虚部,即形式不变。
到此为止,已经弄明白几件事情了:
TransE的缺陷RoratE的改进想法Hadmard product满足三种关系的表达需求Hadmard product的计算可以看成是复平面中embedding的相乘
还有一件事情,复平面中embedding的相乘和欧拉公式有啥关系?
我们使用了Hadmard product将一个head实体变成了tail实体,其中的一个操作用来衡量关系,在复空间中将一个实体变成另一个实体,使用的是乘法的方式,那就是指数了,而指数与复空间建立关系的途径,就是欧拉公式。
$$
e^{i\theta} = \text{cos}\theta + i\text{sin}\theta
$$
复空间中的每个数有指数形式和极坐标形式,这两者之间的关系也是欧拉公式。
从指数形式来看,将一个复数的embedding变换成另一个复数的embedding如下:
$$e^{i{\Theta}_h} e^{i{\Theta}_r} = e^{i{\Theta}_t}$$
用极坐标表示,就是将$e^{i{\Theta}_h}$ 逆时针方向旋转了角度 $\Theta_r$,变成了 $e^{i{\Theta}_t}$ 。
当将关系写成极坐标形式时,
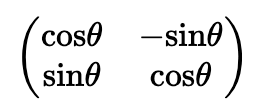
也就是如下所示:
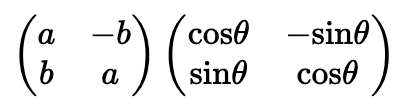
这不就是线性变换里的旋转吗,也就是本文的名称的由来!
不明白的可以回顾一下以前的知识。
因为我们之前约束了关系的模长固定,为1,即 $|r_i| = 1$ 。
因此,在旋转过程中,head实体的模长不会受到影响,只是每一个维度下的复数的相位受到了影响。
训练
For each triple $(h, r, t)$ , we define the distance function of RotatE as:
$$d_r (\mathbf{h}, \mathbf{t}) = \Vert \mathbf{h} \circ \mathbf{r} − \mathbf{t} \Vert$$
Loss函数
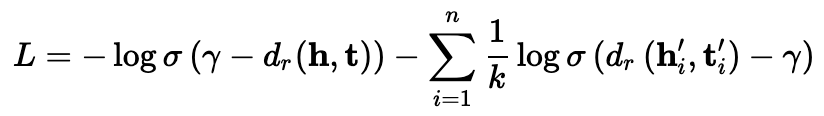
- $\gamma$ : 和
TransE中一样,是margin,视为超参数; - $\sigma$ :
sigmoid function - $(h_i , r, t_i )$ is the
i-th negative triplet. - $k$ 为embedding dimension
采样
原来的采样方式是使用均匀的方式替换head和tail:
低效
suffers the problem of inefficiency since many samples are obviously false as training goes on
没有足够的信息
not provide any meaningful information.
文中提出self-adversarial negative sampling,具体而言就是按照以下方式进行采样,
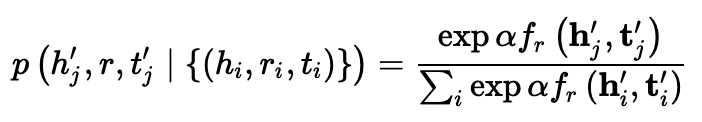
$\alpha$ : temperature of sampling.
Moreover, since the sampling procedure may be costly, we treat the above probability as the weight of the negative sample. Therefore, the final negative sampling loss with self-adversarial training takes the following form:
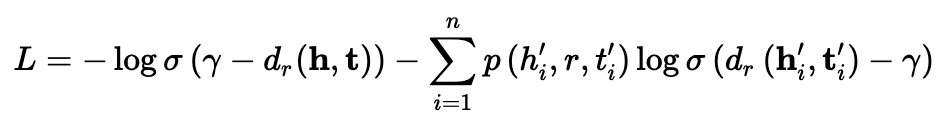
评估
数据集
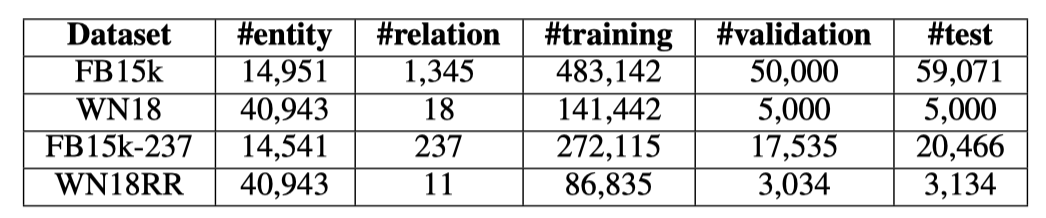
实验设置
Filtered setting: we rank test triples against all other candidate triples not appearing in the training, validation, or test set, where candidates are generated by corrupting subjects or objects: $(h^{‘} , r, t)$ or $(h, r, t^{‘} )$.Mean Rank (MR),Mean Reciprocal Rank (MRR)andHits at N (H@N)are standard evaluation measures for these datasets and are evaluated in our experiments.
超参设置
optimizer:Adamsearch strategy: fine-tune the hyperparameters on the validation dataset withgrid searchembedding dimension: 125, 250, 500, 1000batch size: 512, 1024, 2048- self-adversarial
sampling temperature: 0.5, 1.0 fixed margin$\gamma$ :3, 6, 9, 12, 18, 24, 30. we find that the fixed margin $\gamma$ could prevent our model from over-fitting.
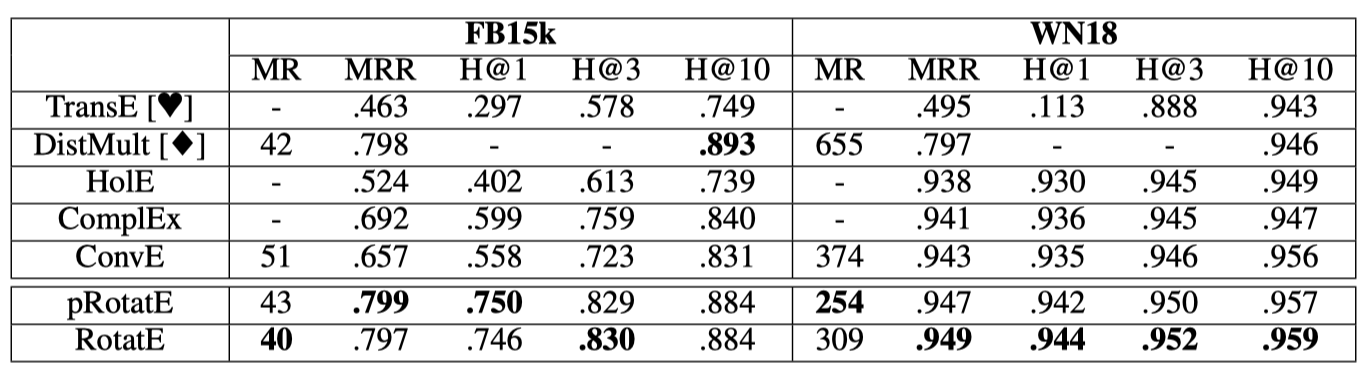
结果
这里主要体现了在3个来源,4个数据集上的评估效果。
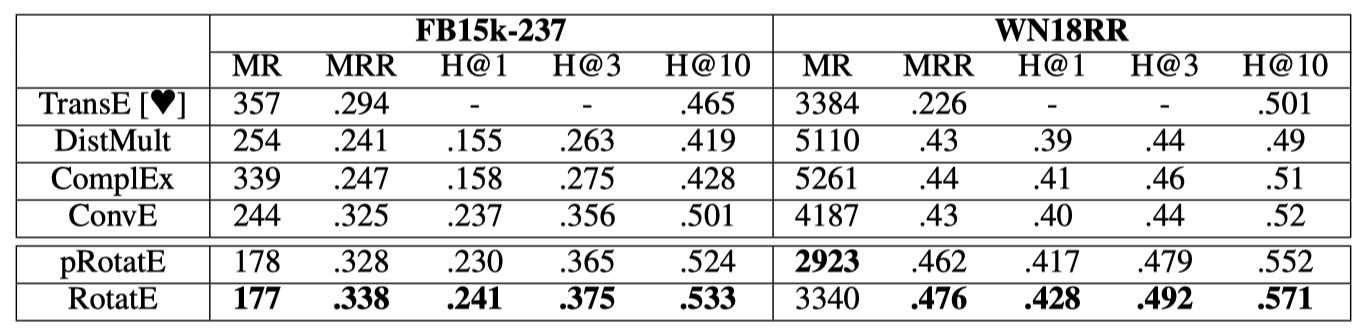
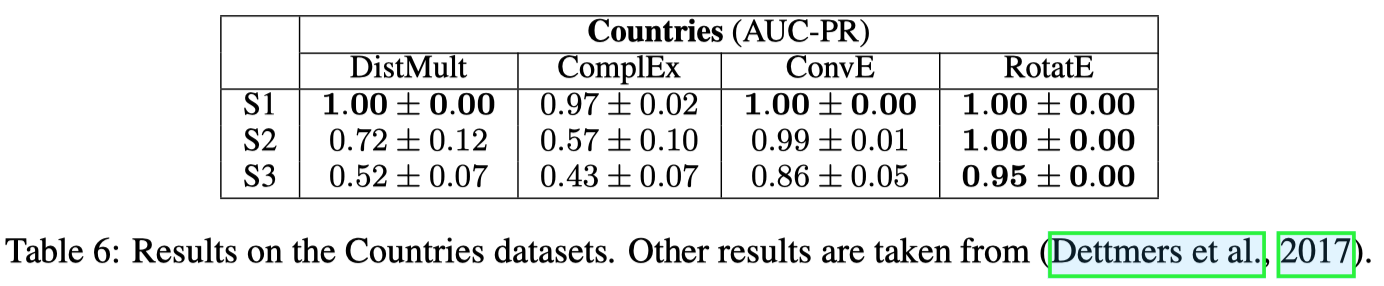
结果总结
本论文主要达成了三项目的:
able to model and infer various relation patterns including: symmetry/antisymmetry, inversion, and composition.
propose a novel self-adversarial negative sampling technique for efficiently and effectively training the RotatE model.
the RotatE model is scalable to large knowledge graphs as it remains linear in both time and memory.

