计算机图形学的预备知识
本节主要是复习了计算机图形学中可能用到的线性代数知识，其实CG中也会用到其他一些知识，包括但不限于：
Basic mathematics
- Linear algebra
- Calculus
- Statistics
Basic physics
- Optics
- Mechanics
Misc
- Signal processing
- Numerical analysis
And a bit of aesthetics
Vector
简介
- Usually written as $\vec{a}$ or in bold $\textbf{a}$
- Or using start and end points
- Direction and length
- No absolute starting position
Vector Normalization
- Magnitude (length) of a vector written as $|\vec{a}|$
- Unit vector
- A vector with magnitude of 1
- Finding the unit vector of a vector (normalization): $\hat{a}=\vec{a} /|\vec{a}|$
- Used to represent directions
Vector Addition
- Geometrically: Parallelogram law & Triangle law
- Algebraically: Simply add coordinates
Cartesian Coordinates
- X and Y can be any (usually orthogonal unit) vectors $$
\mathbf{A}=\left(\begin{array}{l}x \\ y \end{array}\right) \quad \mathbf{A}^{T}=(x, y) \quad|\mathbf{A}|=\sqrt{x^{2}+y^{2}}
$$ 默认向量是列向量。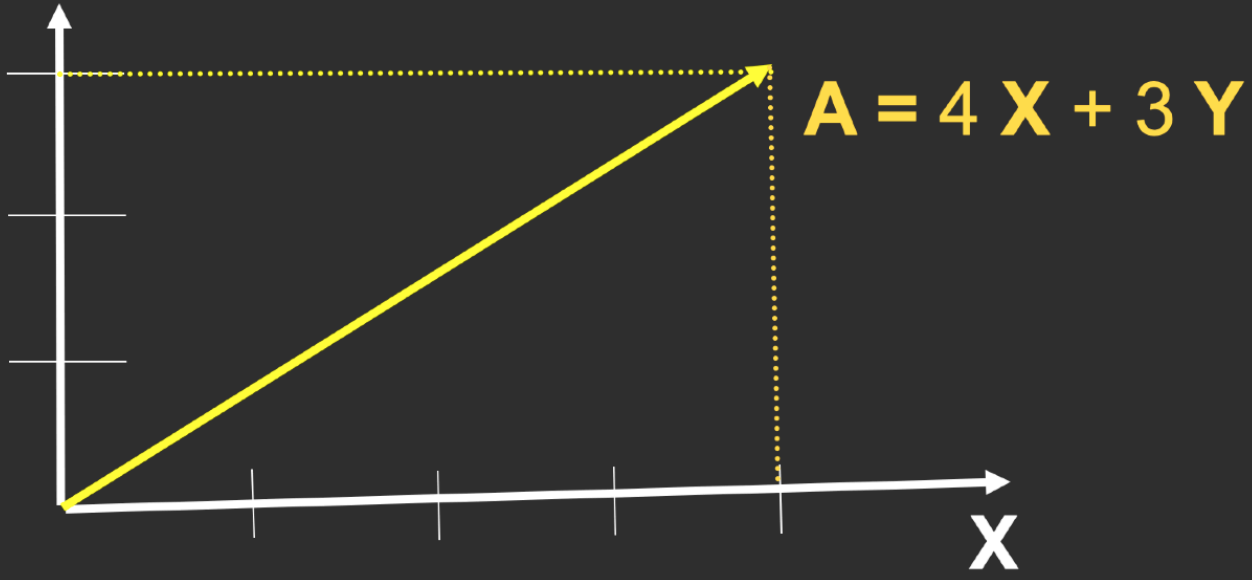
Vector Multiplication
Dot (scalar) Product
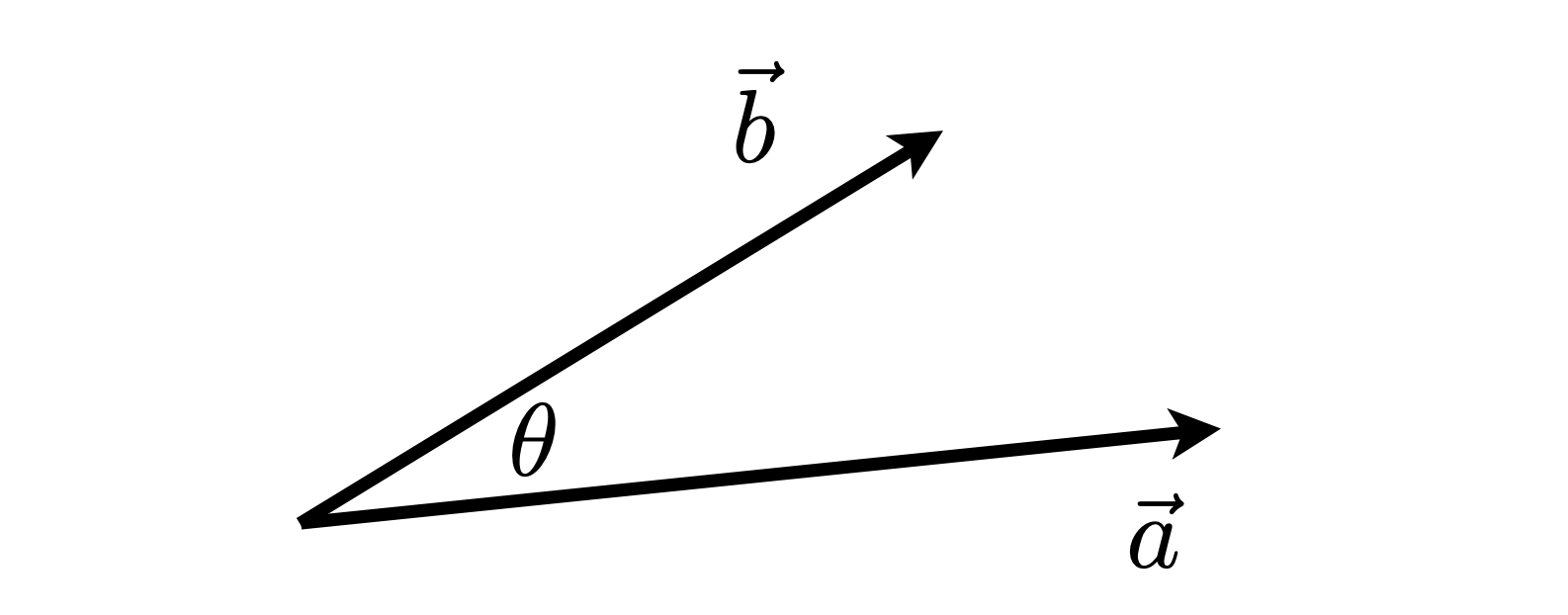
- 定义 $$
\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta
$$ $$
\cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}
$$ - 运算法则： $$
\begin{array}{l} \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} \\
\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} \\ (k \vec{a}) \cdot \vec{b}=\vec{a} \cdot(k \vec{b})=k(\vec{a} \cdot \vec{b})\end{array}
$$ - Dot Product in Cartesian Coordinates Component-wise multiplication, then adding up
- In 2D $$
\vec{a} \cdot \vec{b}=\left(\begin{array}{l}x_{a} \\ y_{a}\end{array}\right) \cdot\left(\begin{array}{l}x_{b} \\ y_{b}\end{array}\right)=x_{a} x_{b}+y_{a} y_{b}
$$ - In 3D $$
\vec{a} \cdot \vec{b}=\left(\begin{array}{c}x_{a} \\ y_{a} \\ z_{a}\end{array}\right) \cdot\left(\begin{array}{c}x_{b} \\ y_{b} \\ z_{b}\end{array}\right)=x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b}
$$
- In 2D $$
Dot Product in Graphics
- Find angle between two vectors, (e.g. cosine of angle between light source and surface)
- Finding projection of one vector on another
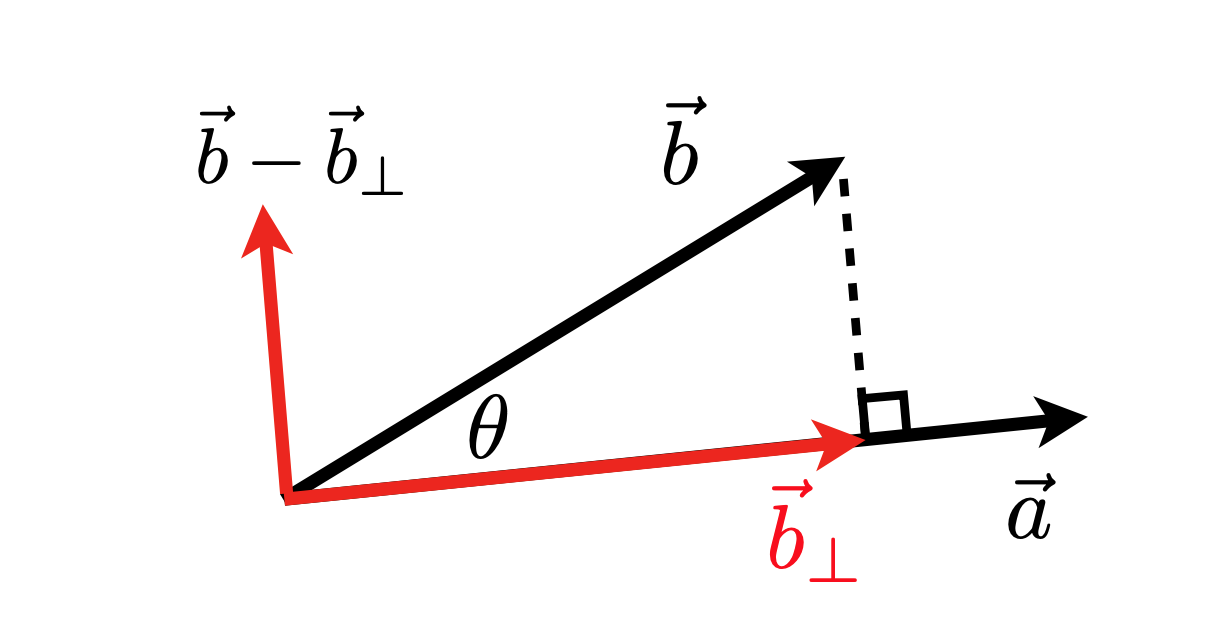$\vec{b}_{\perp}$: projection of $\vec{b}$ onto $\vec{a}$- $\vec{b}_{\perp}$ must be along $\vec{a}$ (or along $\hat{a}$ )
- $\vec{b}_{\perp}=k \hat{a}$
- What’s its magnitude $k$?
- $k=|\vec{b}_{\perp}|=|\vec{b}| \cos \theta$
- 投影可以用来：
- Measure how close two directions are
- Decompose a vector
- Determine forward / backward：明确两个向量的方向性，同向、反向、垂直；
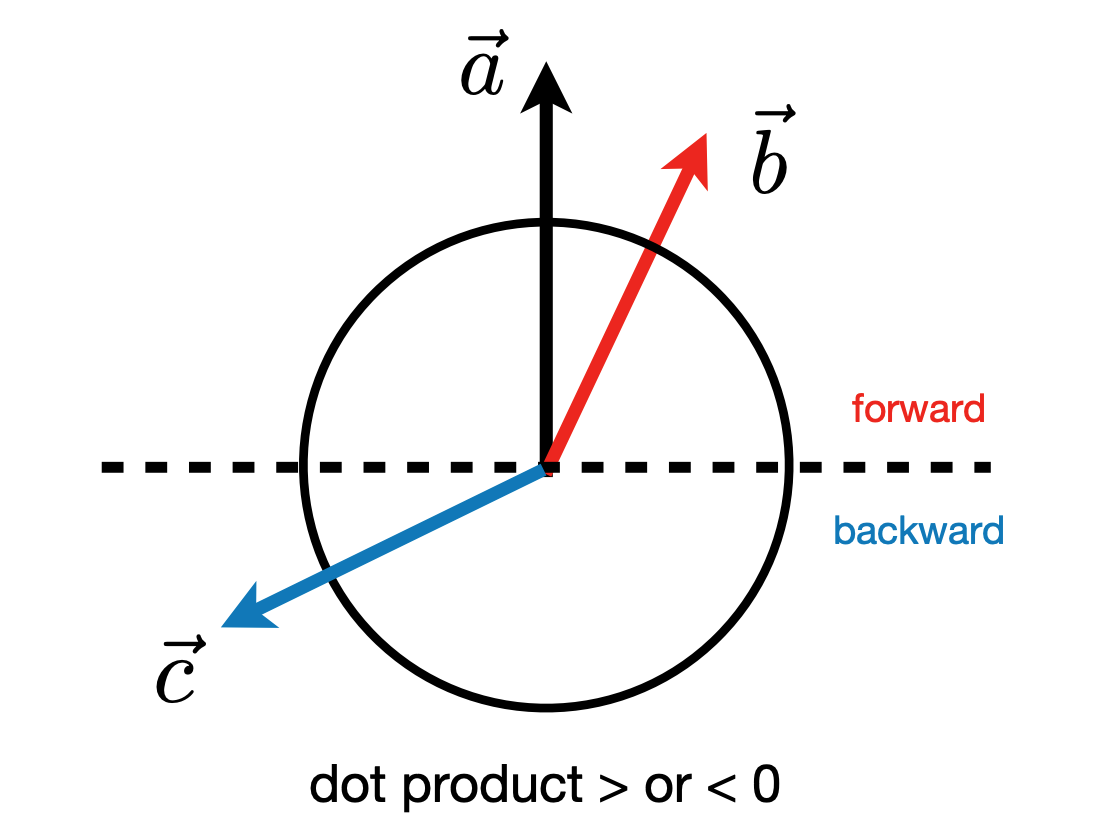
Cross (vector) Product
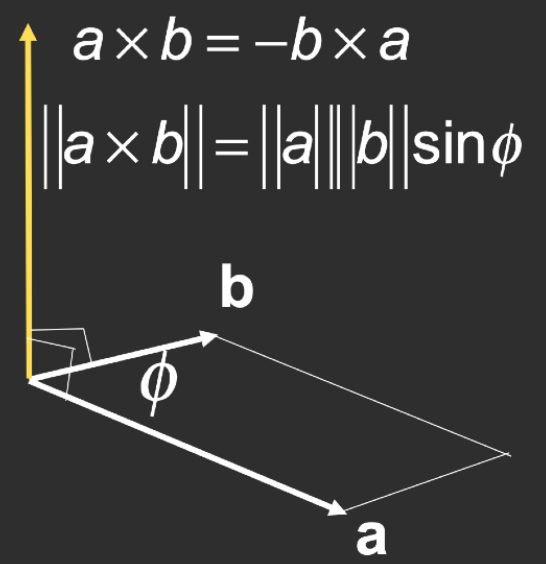
- Cross product is orthogonal to two initial vectors：结果为向量，不是数字；
- Direction determined by right-hand rule
- Useful in constructing coordinate systems：构建的称为右手坐标系；
$$
\begin{array}{l}\vec{x} \times \vec{y}=+\vec{z} \\
\vec{y} \times \vec{x}=-\vec{z} \\
\vec{y} \times \vec{z}=+\vec{x} \\
\vec{z} \times \vec{y}=-\vec{x} \\
\vec{z} \times \vec{x}=+\vec{y} \\
\vec{x} \times \vec{z}=-\vec{y}\end{array}
$$
- 运算性质 $$
\begin{array}{c}\vec{a} \times \vec{b}=-\vec{b} \times \vec{a} \\
\vec{a} \times \vec{a}=\overrightarrow{0} \\
\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} \\
\vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b})\end{array}
$$ - Cross Product: Cartesian Formula $$
\vec{a} \times \vec{b}=\left(\begin{array}{l}y_{a} z_{b}-y_{b} z_{a} \\
z_{a} x_{b}-x_{a} z_{b} \\
x_{a} y_{b}-y_{a} x_{b}\end{array}\right)
$$
Cross Product in Graphics
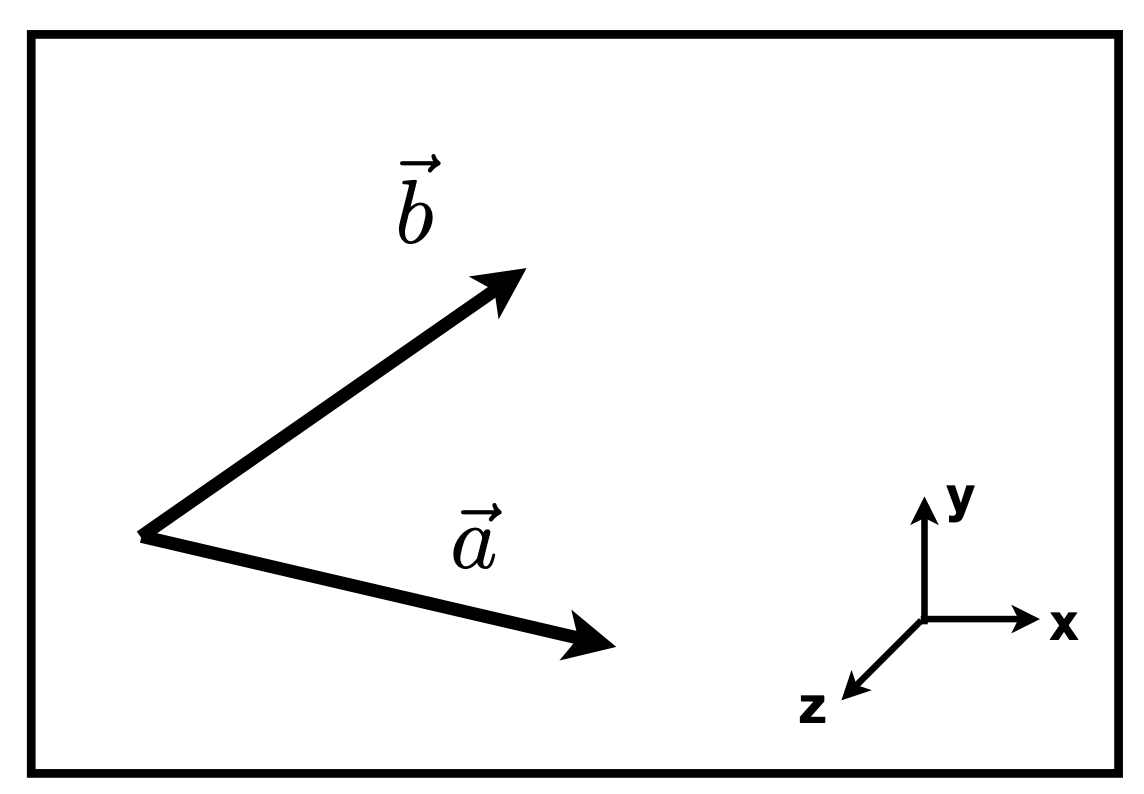
- Determine left / right：$\vec{a} \times \vec{b} > 0$，说明 $\vec{b}$ 在 $\vec{a}$ 的左边；反之在右边；
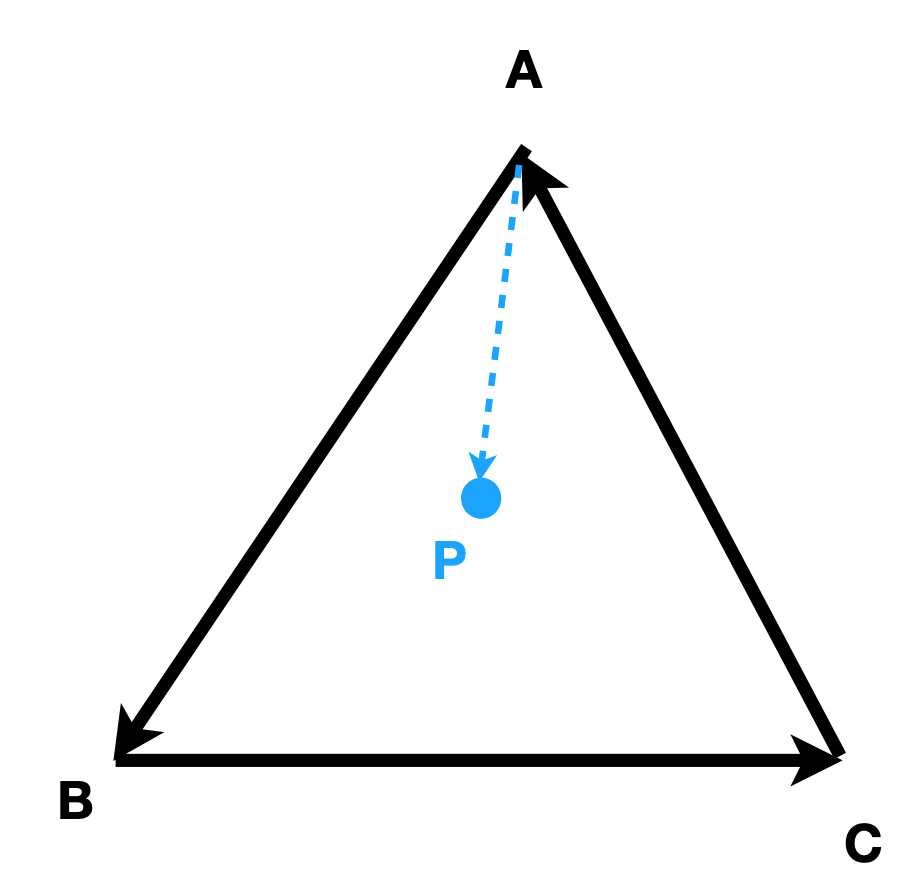
- Determine inside / outside：当$p$点，与三角形各个顶点的连线，$\overrightarrow{AP}$、$\overrightarrow{BP}$、$\overrightarrow{CP}$分别与$\overrightarrow{AB}$、$\overrightarrow{BC}$、$\overrightarrow{CA}$计算Cross Product，如果p点均在三个向量的左侧或者右侧，则该点在三角形内部，若落在边界上可自由处理。
Orthonormal bases and coordinate frames
- Important for representing points, positions, locations
- Often, many sets of coordinate systems
- Global, local, world, model, parts of model (head, hands, …)
- Critical issue is transforming between these systems/bases
有助于将向量进行分解，例如对于右手坐标系：
Any set of 3 vectors (in 3D) that
$$
\begin{array}{l}|\vec{u}|=|\vec{v}|=|\vec{w}|=1 \\
\vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{w}=\vec{u} \cdot \vec{w}=0 \\
\vec{w}=\vec{u} \times \vec{v} \quad \text { (right-handed) } \\
\vec{p}=(\vec{p} \cdot \vec{u}) \vec{u}+(\vec{p} \cdot \vec{v}) \vec{v}+(\vec{p} \cdot \vec{w}) \vec{w} \\
\text { (projection) }\end{array}
$$
Matrices
- In Graphics, pervasively used to represent transformations
- Array of numbers (m × n = m rows, n columns) $$
\left(\begin{array}{ll}1 & 3 \\ 5 & 2 \\ 0 & 4 \end{array}\right)
$$ - Addition and multiplication by a scalar are trivial: element by element
Matrix-Matrix Multiplication
- (number of) columns in A must = # rows in B
- (M x N) (N x P) = (M x P) $$
\left(\begin{array}{ll}1 & 3 \\ 5 & 2 \\ 0 & 4\end{array}\right)\left(\begin{array}{llll}3 & 6 & 9 & 4 \\ 2 & 7 & 8 & 3\end{array}\right)
$$ - Element (i, j) in the product is the dot product of row i from A and column j from B
- 运算规则
- Non-commutative: (AB and BA are different in general)
- Associative and distributive
- (AB)C=A(BC)
- A(B+C) = AB + AC
- (A+B)C = AC + BC
Matrix-Vector Multiplication
Treat vector as a column matrix (m×1)
$$
\left(\begin{array}{cc}-1 & 0 \\ 0 & 1\end{array}\right)\left(\begin{array}{l}x \\ y \end{array}\right)=\left(\begin{array}{c}-x \\ y \end{array}\right)
$$
Transpose of a Matrix
Switch rows and columns (ij -> ji)
$$
\left(\begin{array}{ll}1 & 2 \\ 3 & 4 \\ 5 & 6\end{array}\right)^{T}=\left(\begin{array}{lll}1 & 3 & 5 \\ 2 & 4 & 6\end{array}\right)
$$
运算性质：
$$
(A B)^{T}=B^{T} A^{T}
$$
Identity Matrix and Inverses
$$
I_{3 \times 3}=\left(\begin{array}{ccc}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right)
$$
$$
\begin{array}{l}A A^{-1}=A^{-1} A=I \\ (A B)^{-1}=B^{-1} A^{-1}\end{array}
$$
Vector multiplication in Matrix form
Dot product
$$
\begin{aligned}\vec{a} \cdot \vec{b} \\ =&\vec{a}^{T} \vec{b} \\ =&\left(\begin{array}{lll}x_{a} & y_{a} & z_{a}\end{array}\right)\left(\begin{array}{c}x_{b} \\ y_{b} \\ z_{b}\end{array}\right)=\left(x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b}\right)\end{aligned}
$$
Cross product
$$
\vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc}0 & -z_{a} & y_{a} \\ z_{a} & 0 & -x_{a} \\ -y_{a} & x_{a} & 0\end{array}\right)\left(\begin{array}{l}x_{b} \\ y_{b} \\ z_{b}\end{array}\right)
$$
A: dual matrix of vector a
