Linear Transforms = Matrices
Scale Transform
变换操作为:
$$
\text{scale}(s_x, s_y) = \left(\begin{array}{ll}s_x & 0 \\ 0 & s_y \end{array}\right)
$$
在点$(x, y)$经过变换后变为$(x^{\prime}, y^{\prime})$,如下:
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)=\left(\begin{array}{ll}
s_x & 0 \\
0 & s_y
\end{array}\right) \left(\begin{array}{l}
x \\
y
\end{array}\right) = \left(\begin{array}{l}
s_xx \\
s_yy
\end{array}\right)
$$
Reflection Transform
在水平方向上,其实是沿y轴翻转。
$$
x^{\prime} = -x \\
y^{\prime} = y
$$
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)=\left(\begin{array}{ll}
-1 & 0 \\
0 & 1
\end{array}\right) \left(\begin{array}{l}
x \\
y
\end{array}\right) = \left(\begin{array}{l}
-x \\
y
\end{array}\right)
$$
在竖直方向上,其实是沿x轴翻转。
$$
x^{\prime} = x \\
y^{\prime} = -y
$$
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)=\left(\begin{array}{ll}
1 & 0 \\
0 & -1
\end{array}\right) \left(\begin{array}{l}
x \\
y
\end{array}\right) = \left(\begin{array}{l}
x \\
-y
\end{array}\right)
$$
Shear Transform
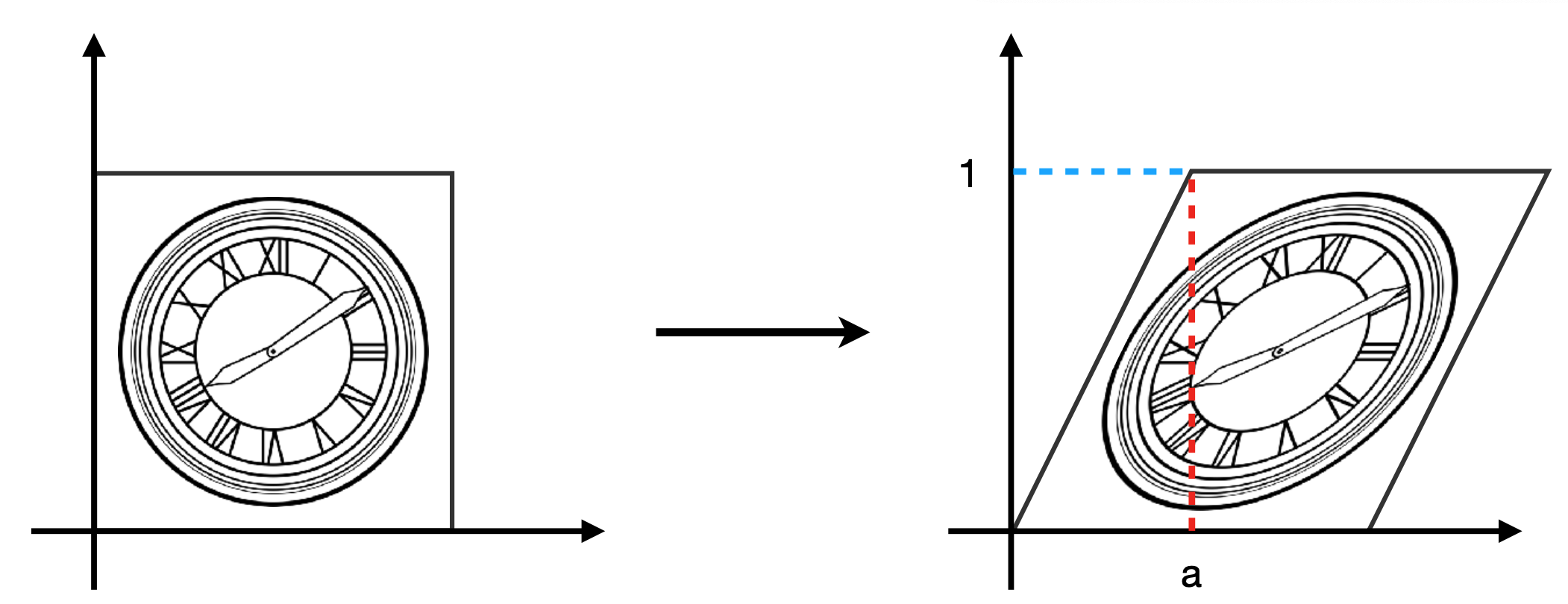
在水平方向上,纵坐标不变化。
$$
x^{\prime} = x + ay \\
y^{\prime} = y
$$
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)=\left(\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right) \left(\begin{array}{l}
x \\
y
\end{array}\right) = \left(\begin{array}{l}
x + ay \\
y
\end{array}\right)
$$
在竖直方向上,横坐标不变化。
$$
x^{\prime} = x \\
y^{\prime} = y + ax
$$
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)=
\left(\begin{array}{ll}
1 & 0 \\
a & 1
\end{array}\right) \left(\begin{array}{l}
x \\
y
\end{array}\right) = \left(\begin{array}{l}
x \\
y + ax
\end{array}\right)
$$
Rotate Transform
默认规则
- about the origin (0, 0):围绕原点旋转;
- CCW by default:默认是逆时针旋转;
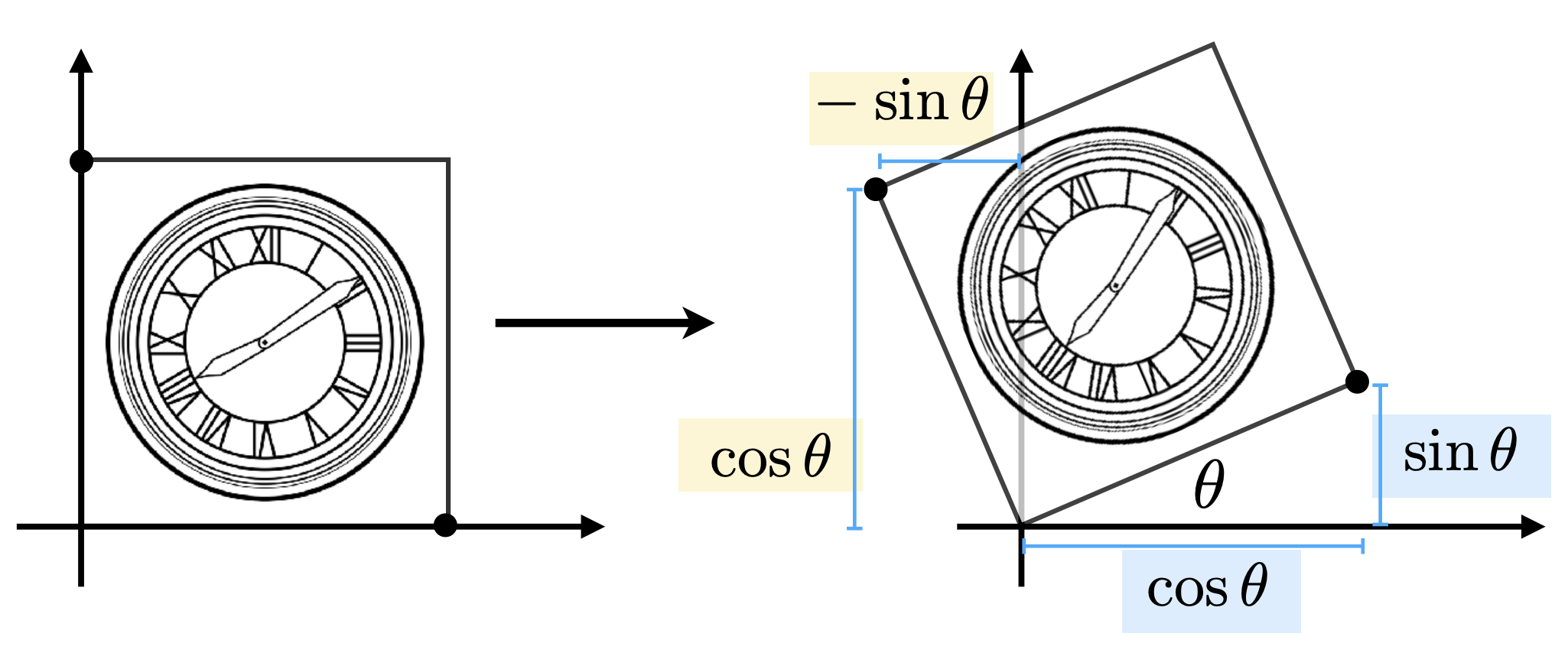
取图中两个特殊点计算旋转矩阵,得到:
$$
\mathbf{R}_{\theta} = \left(\begin{array}{ll}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{array}\right)
$$
特殊性质
$$
\mathbf{R_{-\theta}} =
\left(\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right) = \mathbf{R_{\theta}^{\top}}
$$
根据定义:
$$
\mathbf{R_{-\theta}}=\mathbf{R_{\theta}^{-1}}
$$
因此得到:
$$
\mathbf{R_{\theta}^{\top}}=\mathbf{R_{\theta}^{-1}}
$$
这一性质表明旋转矩阵是正交矩阵。
Linear Transform总结
其中对应矩阵的维度与点的维度保持一致。
$$
x^{\prime} = ax + by \\
y^{\prime} = cx + dy
$$
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)=\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \left(\begin{array}{l}
x \\
y
\end{array}\right) = \left(\begin{array}{l}
ax + by \\
cx + dy
\end{array}\right)
$$
$$
x^{\prime} = Mx
$$
Homogeneous coordinates
为啥要用齐次坐标?
要解决平移变换的问题,将之与之前的变换统一表示,因为不能将平移变换写成矩阵乘法的形式。
Translation Transform
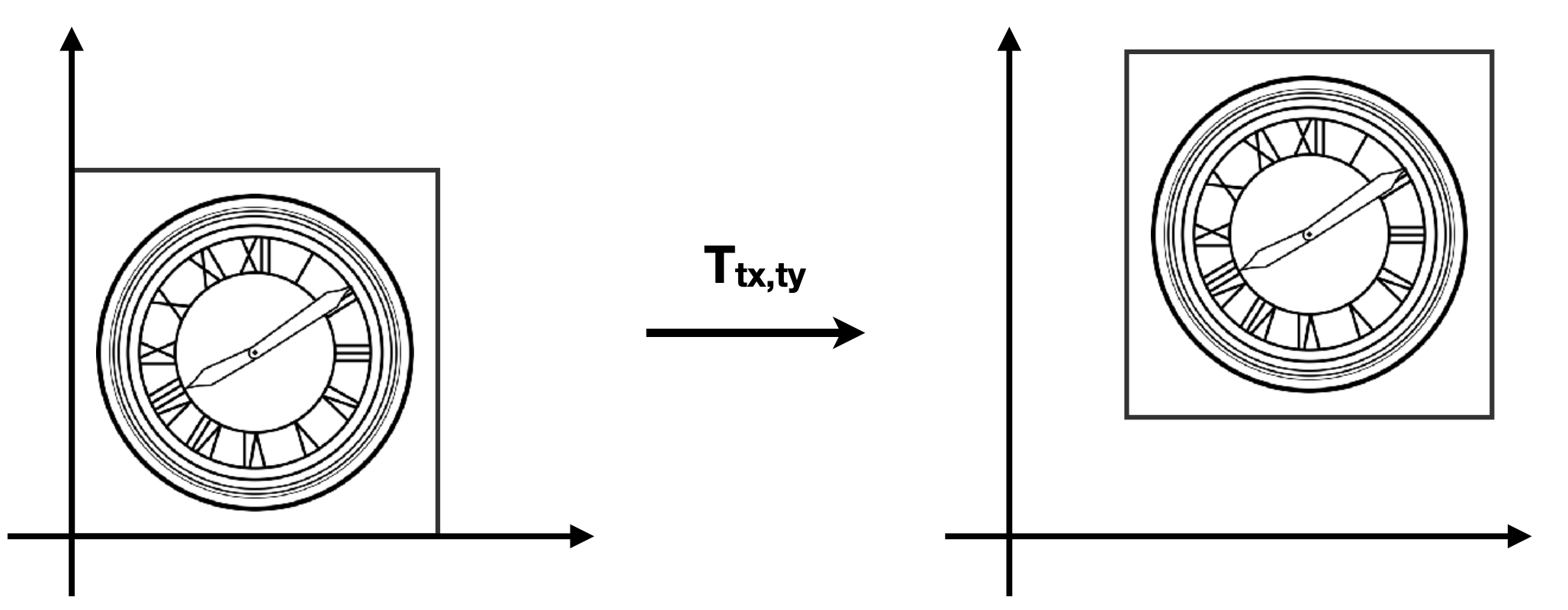
$$
x^{\prime} = x + t_x \\
y^{\prime} = y + t_y
$$
Translation cannot be represented in matrix form. 不是线性变换。
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)=
\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)
\left(\begin{array}{l}
x \\
y
\end{array}\right)
+
\left(\begin{array}{l}
t_x \\
t_y
\end{array}\right)
$$
由于不想将该变换特殊处理,为了统一表示,因此需要齐次坐标。
Solution: Homogenous Coordinates
Add a third coordinate (w-coordinate)
- 2D point = $(x, y, 1)^T$
- 2D vector = $(x, y, 0)^T$
为啥点和向量在增加的坐标上的表示分别为1和0,而不是相同呢?因为向量具有平移不变性,而点经过平移则会发生变化。
Valid operation if w-coordinate of result is 1 or 0:
- vector + vector = vector
- point – point = vector
- point + vector = point
- point + point = ??
In homogeneous coordinates,
$$
\left(\begin{array}{l}
x \\
y \\
w
\end{array}\right)
$$
is the 2D point
$$
\left(\begin{array}{l}
x/w \\
y/w \\
1
\end{array}\right)
$$
$$w \ne 0. $$
在该扩充定义下,齐次坐标中,两点之间的加和结果是两个点的中点,还是一个点。
齐次坐标的代价:引入了多余的数字,理论上会增加存储,但是实际中可以不管。
Translation在齐次坐标下的表示
使用该方法表示Translation得到:
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
w^{\prime}
\end{array}\right)=
\left(\begin{array}{lll}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{array}\right) \left(\begin{array}{l}
x \\
y \\
1
\end{array}\right)
= \left(\begin{array}{l}
x + t_x \\
y + t_y \\
1
\end{array}\right)
$$
从而实现转化为矩阵乘法的形式。
Affine Transform仿射变换
Affine map = linear map + translation
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)
=
\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)
\left(\begin{array}{l}
x \\
y
\end{array}\right)
+
\left(\begin{array}{l}
t_x \\
t_y
\end{array}\right)
$$
在齐次坐标下表示如下:
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
1
\end{array}\right)
=
\left(\begin{array}{lll}
a & b & t_x \\
c & d & t_y \\
0 & 0 & 1
\end{array}\right) \cdot
\left(\begin{array}{l}
x \\
y \\
1
\end{array}\right)
$$
齐次坐标下统一表示
Scale
$$
\mathbf{S}(s_x, s_y) =
\left(\begin{array}{ll}
s_x & 0 & 0 \\
0 & s_y & 0 \\
0&0& 1
\end{array}\right)
$$
Rotation
$$
\mathbf{R}(\theta) = \left(\begin{array}{ll}
\cos\theta & -\sin\theta & 0 \\
\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{array}\right)
$$
Translation
$$
\mathbf{T}(t_x, t_y) =
\left(\begin{array}{lll}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{array}\right)
$$
Inverse Transform
逆变换 $M$ 在数学上等价于乘上逆矩阵。$M^{-1}$ is the inverse of transform in both a matrix and geometric sense。
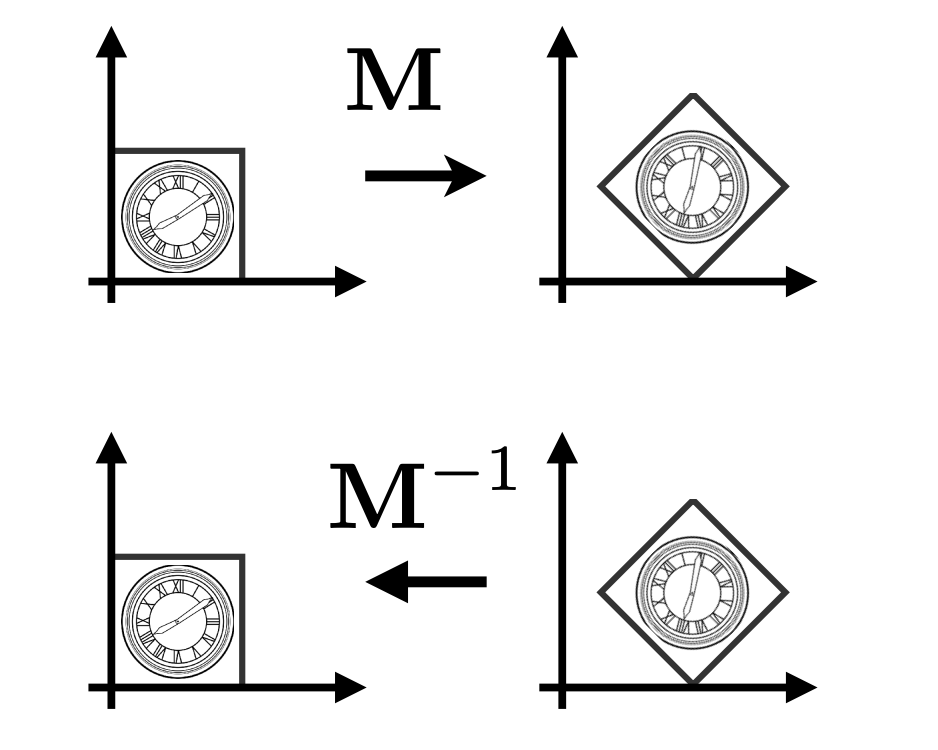
Composite Transform
具体实践
在组合不同的变换时,注意:Transform Ordering Matters。
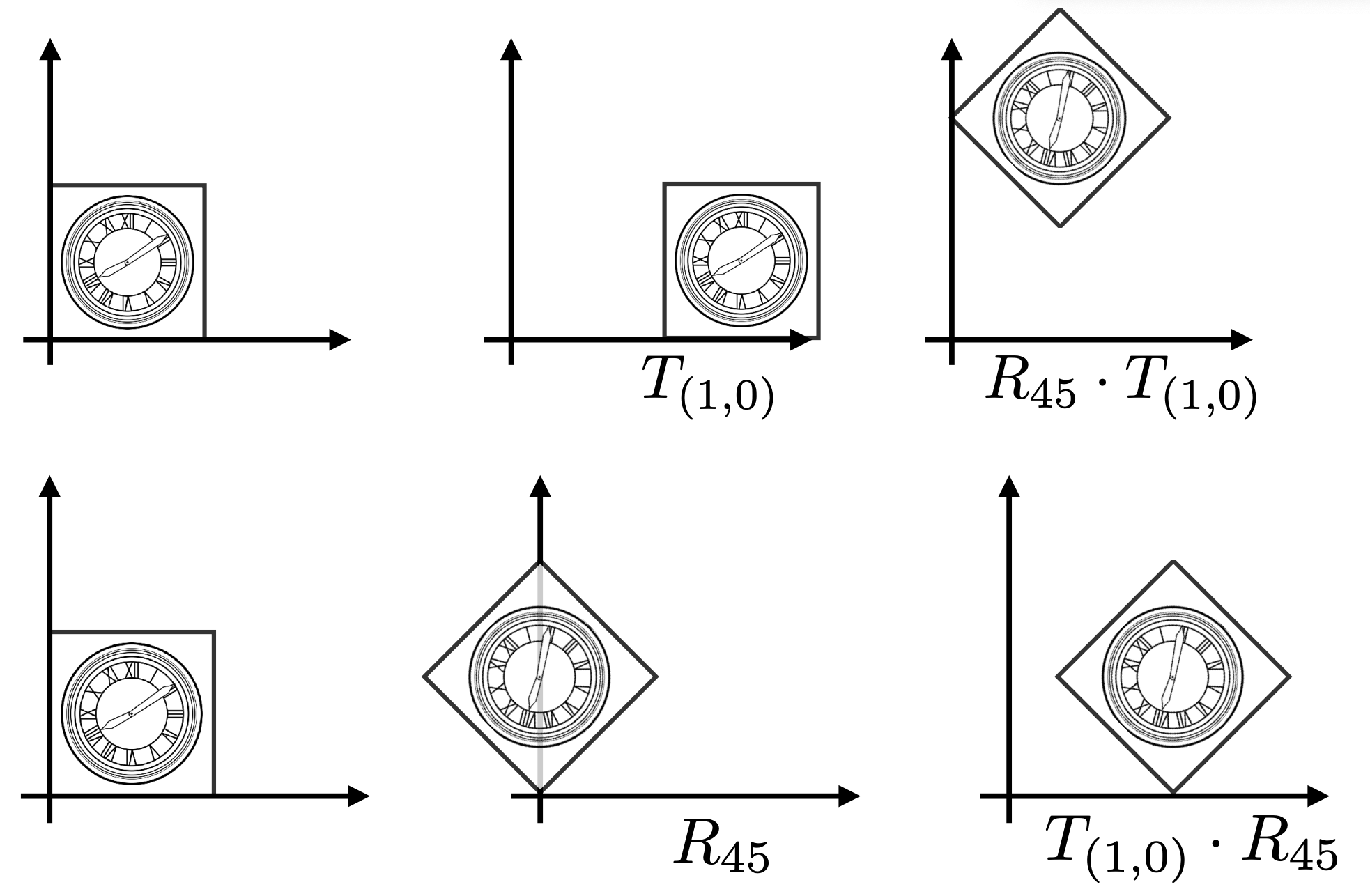
如何理解?
Matrix multiplication is not commutative.
$$
R_{45} \cdot T_{(1,0)} \ne T_{(1,0)} \cdot R_{45}
$$
Note that matrices are applied right to left:
$$
T_{(1,0)} \cdot R_{45}
\left(\begin{array}{l}x \\ y
\\
1
\end{array}
\right)
=
\left(\begin{array}{lll}1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}
\right)
\left(
\begin{array}{ccc}\cos 45^{\circ} & -\sin 45^{\circ} & 0
\\
\sin 45^{\circ} & \cos 45^{\circ} & 0 \\
0 & 0 & 1\end{array}
\right)
\left(\begin{array}{l}x \\ y \\ 1
\end{array}\right)
$$
对于矩阵乘法来说,当考虑到变换时,是从右到左依次起作用的。
推广
Sequence of affine transforms $A_1, A_2, A_3,$
Compose by matrix multiplication将所有的变换结合起来形成一个变换矩阵然后再统一与原始点相乘。
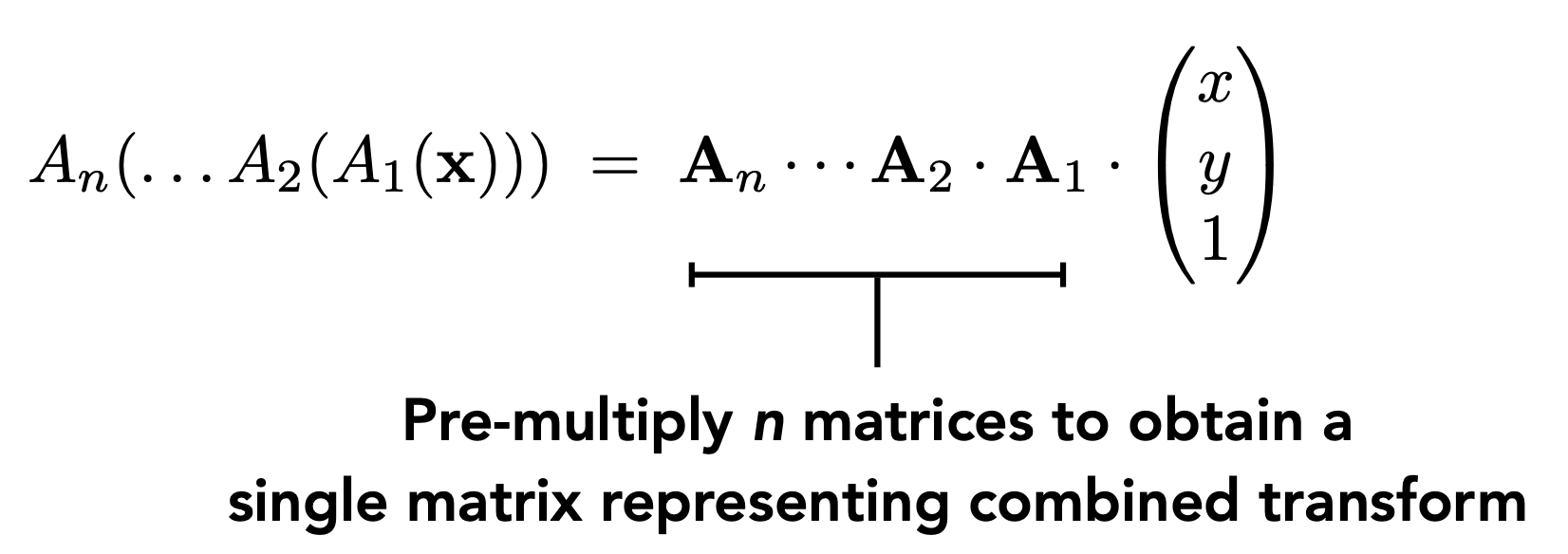
这一技巧对于性能计算很重要,Very important for performance。
Decomposing Complex Transforms
例子:沿着特定点旋转
How to rotate around a given point c?
- Translate center to origin
- Rotate
- Translate back
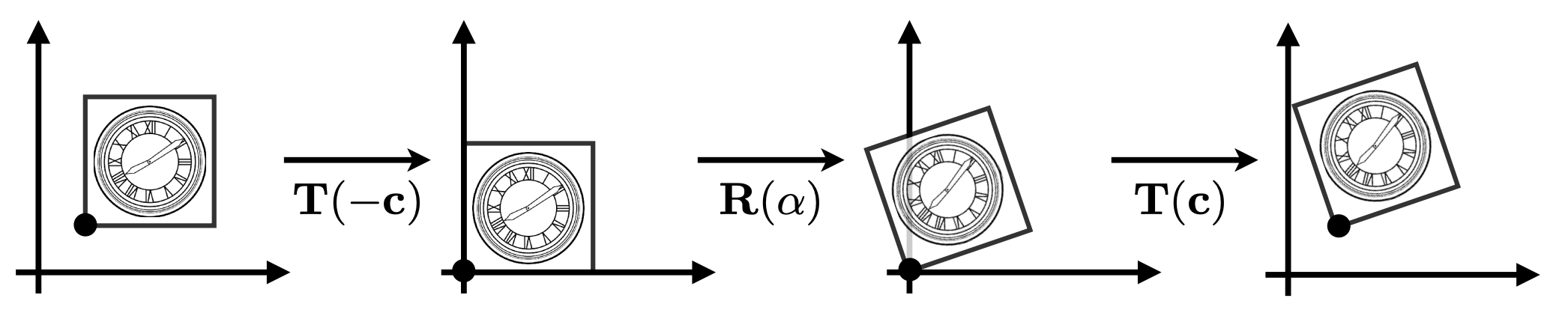
矩阵形式如下:(从右到左依次写)
$$
\mathbf{T}(c) \cdot \mathbf{R}(\alpha) \cdot \mathbf{T}(-c)
$$
