Homogeneous coordinates
- 3D point = $(x, y, z, 1)^T$
- 3D vector = $(x, y, z, 0)^T$
对应的,坐标 $(x,y,z,w)(w \ne 0)$ 表示三维空间中的点$(x/w, y/w, z/w)$。
Affine Transform仿射变换
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime} \\
1
\end{array}\right)=
\left(\begin{array}{lll}
a & b & c & t_x \\
d & e & f & t_y \\
g & h & i & t_z \\
0 & 0 & 0 & 1
\end{array}\right) \cdot
\left(\begin{array}{l}
x \\
y \\
z \\
1
\end{array}\right)
$$
What’s the order? Linear Transform first or Translation first.
在操作变换时,首先进行线性变换,之后才进行平移变换。
$$
\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)
=
\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)
\left(\begin{array}{l}
x \\
y
\end{array}\right)
+
\left(\begin{array}{l}
t_x \\
t_y
\end{array}\right)
$$
3D transformations统一表示
Scale
$$
\mathbf{S}(s_x, s_y, s_z) =
\left(\begin{array}{ll}
s_x & 0 & 0 & 0 \\
0 & s_y & 0 & 0 \\
0 & 0 & s_z & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
$$
Translation
$$
\mathbf{T}(t_x, t_y) =
\left(\begin{array}{lll}
1 & 0 & 0 & t_x \\
0 & 1 & 0 & t_y \\
0 & 0 & 1 & t_z \\
0 & 0 & 0 & 1
\end{array}\right)
$$
Rotation
Rotation around x-, y-, or z-axis.
$$
\begin{array}{l}
\mathbf{R_x}(\alpha)=
\left(\begin{array}{cccc}1 & 0 & 0 & 0 \\
0 & \cos \alpha & -\sin \alpha & 0 \\
0 & \sin \alpha & \cos \alpha & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\\
\mathbf{R_y}(\alpha)=
\left(\begin{array}{cccc}\cos \alpha & 0 & \sin \alpha & 0 \\
0 & 1 & 0 & 0 \\
-\sin \alpha & 0 & \cos \alpha & 0 \\
0 & 0 & 0 & 1\end{array}\right)
\\
\mathbf{R_z}(\alpha)=\left(\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0 & 0 \\
\sin \alpha & \cos \alpha & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\end{array}
$$
其中$\mathbf{R}_{y}(\alpha)$会有一些奇怪,因为根据右手螺旋定则,$z$ 与 $x$ 叉乘得到 $y$,$x$ 与 $z$ 叉乘得到 $-y$,这是其在$\sin \alpha$上符号与其他两个相反的原因。(使用左手螺旋也会存在特殊的轴)
3D Rotations
Compose any 3D rotation from $R_x, R_y, R_z$?
$$
\mathbf{R_{xyz}}(\alpha, \beta, \gamma) = \mathbf{R_x}(\alpha)\mathbf{R_y}(\beta)\mathbf{R_z}(\gamma)
$$
其中,三个角度$\alpha, \beta, \gamma$ 称为Euler angles。
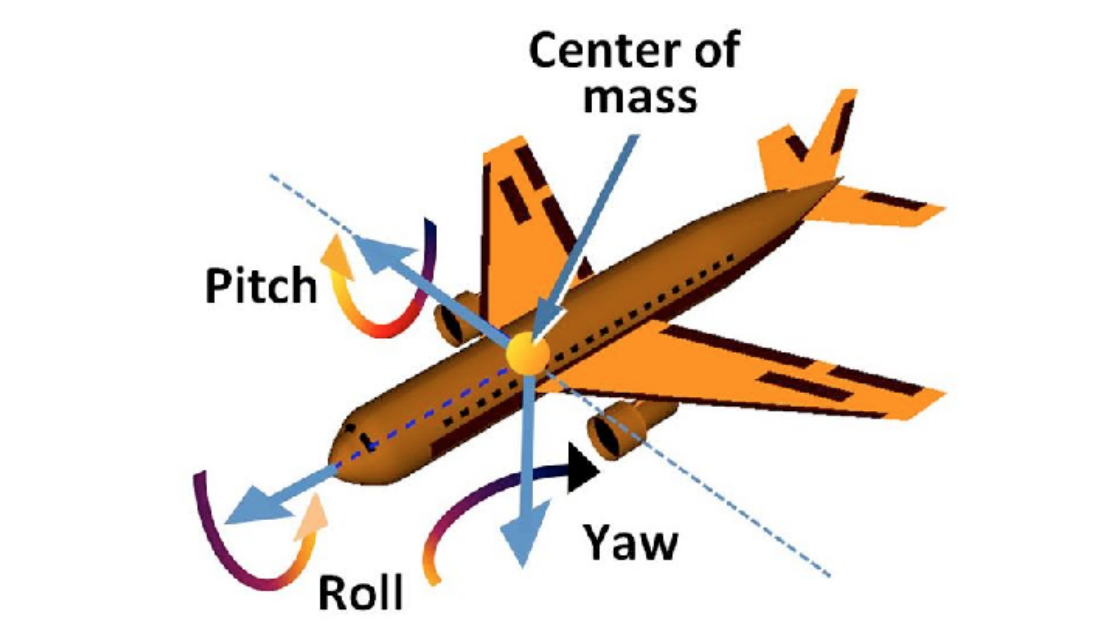
一个典型的应用场景:Often used in flight simulators: roll, pitch, yaw。
Rodrigues’ Rotation Formula
Rotation by angle $\alpha$ around axis $\mathbf{n}$.
$$
\mathbf{R}(\mathbf{n}, \alpha)=
\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc}0 & -n_{z} & n_{y} \\
n_{z} & 0 & -n_{x} \\
-n_{y} & n_{x} & 0
\end{array}\right)}_{\mathbf{N}}
$$
- 其中axis默认是过原点的;
- 当轴不过原点可以利用之前的方法:将所有的东西移动到原点,再旋转,然后再移回去;
- 其中$\mathbf{N}$是向量的叉乘,只是表示成矩阵形式。

