Viewing Transformation指的是将3D中的物体映射到2D中的图像的过程。
例子说明
Think about how to take a photo?
- Find a good place and arrange people (model transformation)
- Find a good “angle” to put the camera (view transformation)
- Cheese! (projection transformation)
View / Camera Transformation
确定相机位置
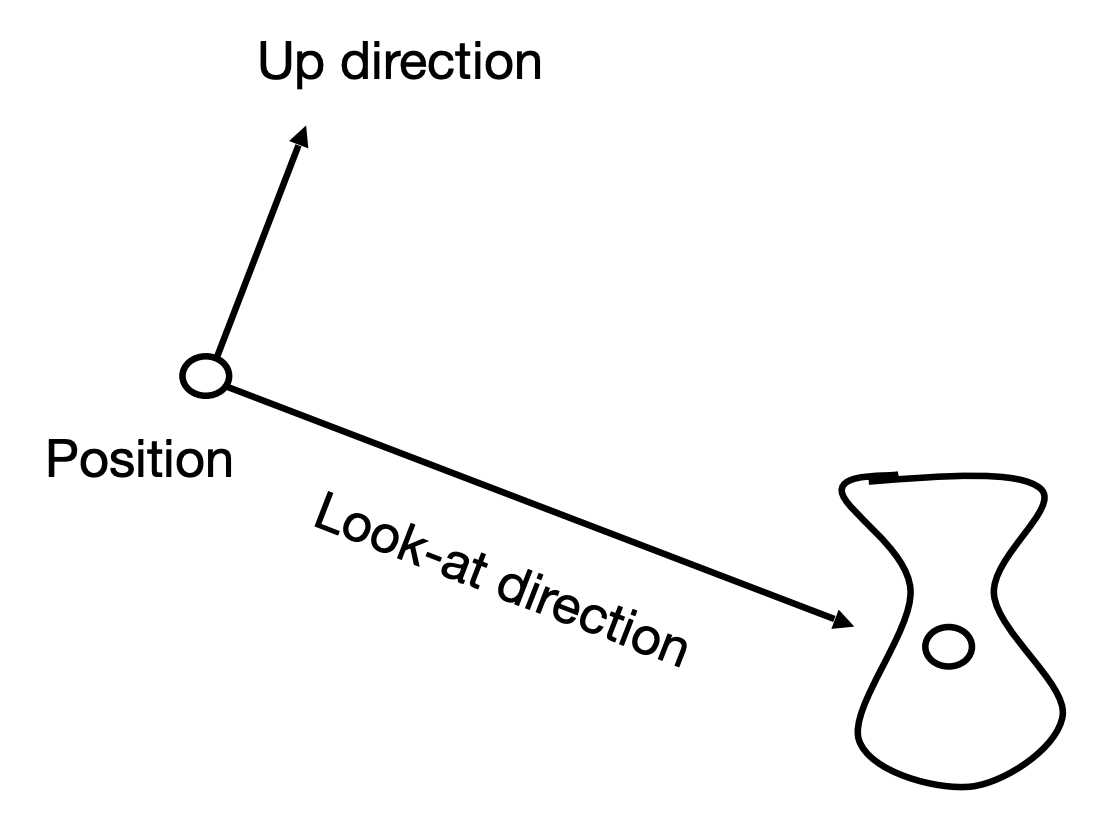
Define the camera first
- Position: $\vec{e}$
- Look-at / gaze direction $\hat{g}$
- Up direction (assuming perp. to look-at): $\hat{t}$
永久固定相机位置
前提
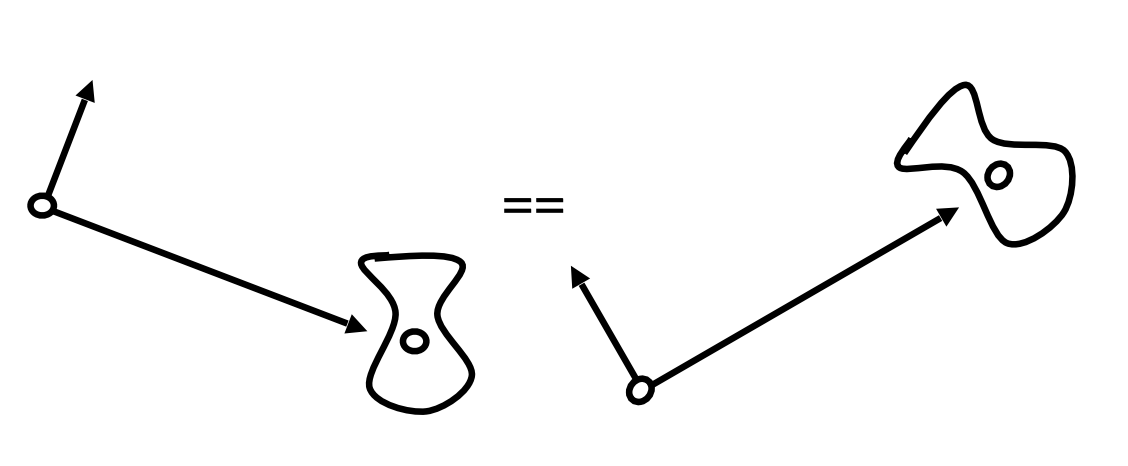
If the camera and all objects move together, the “photo” will be the same.
具体规则
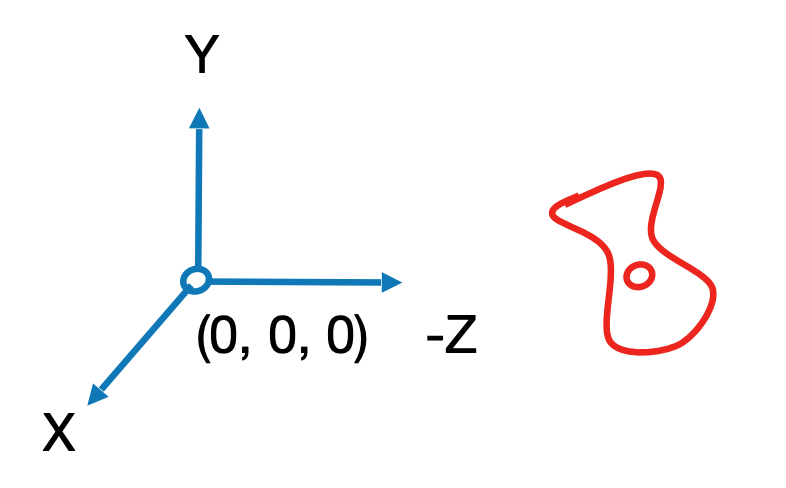
How about that we always transform the camera to
- The origin, up at $Y$, look at $-Z$
- And transform the objects along with the camera
具体变换
Transform the camera by $M_{view}$.
- So it’s located at the origin, up at Y, look at -Z
$M_{view}$ in math?
$$
\mathbf{M_{view}} = \mathbf{R_{view}} \mathbf{T_{view}}
$$
- Translates $\vec{e}$ to origin. $$
\mathbf{T}_{view} =
\left(\begin{array}{lll}
1 & 0 & 0 & -x_e \\
0 & 1 & 0 & -y_e \\
0 & 0 & 1 & -z_e \\
0 & 0 & 0 & 1
\end{array}\right)
$$ - Rotates $g$ to $-Z$, Rotates $t$ to $Y$, Rotates $(g \times t)$ To $X$.
- Consider its inverse rotation: $X$ to $(g \times t)$, $Y$ to $t$, $Z$ to $-g$
\mathbf{R_{view}}^{-1}=
\left(\begin{array}{cccc}x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0 \\
y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0 \\
z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\\
\mathbf{R_{view}}=
\left(\begin{array}{cccc}x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\
x_{t} & y_{t} & z_{t} & 0 \\
x_{-g} & y_{-g} & z_{-g} & 0 \\
0 & 0 & 0 & 1\end{array}\right)
$$ 利用了旋转矩阵为正交矩阵的性质。
总结
- 上述整个过程也可以称为ModelView Transformation,因为相机和物体可以同时变化。
- 该过程为投影变换奠定基础。
Projection transformation
简介
Projection in Computer Graphics
- Orthographic projection:相机无限远,平行线仍平行
- Perspective projection:相机有限远,近大远小,平行线会相交,更符合现实;
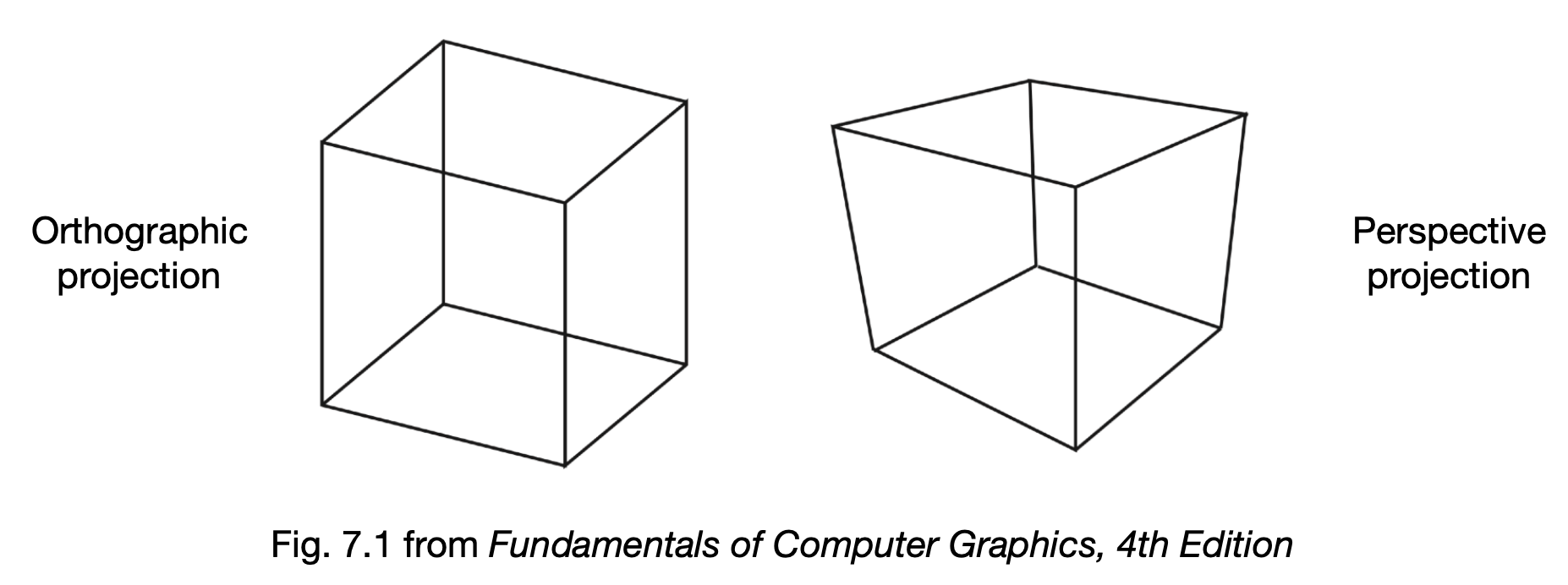
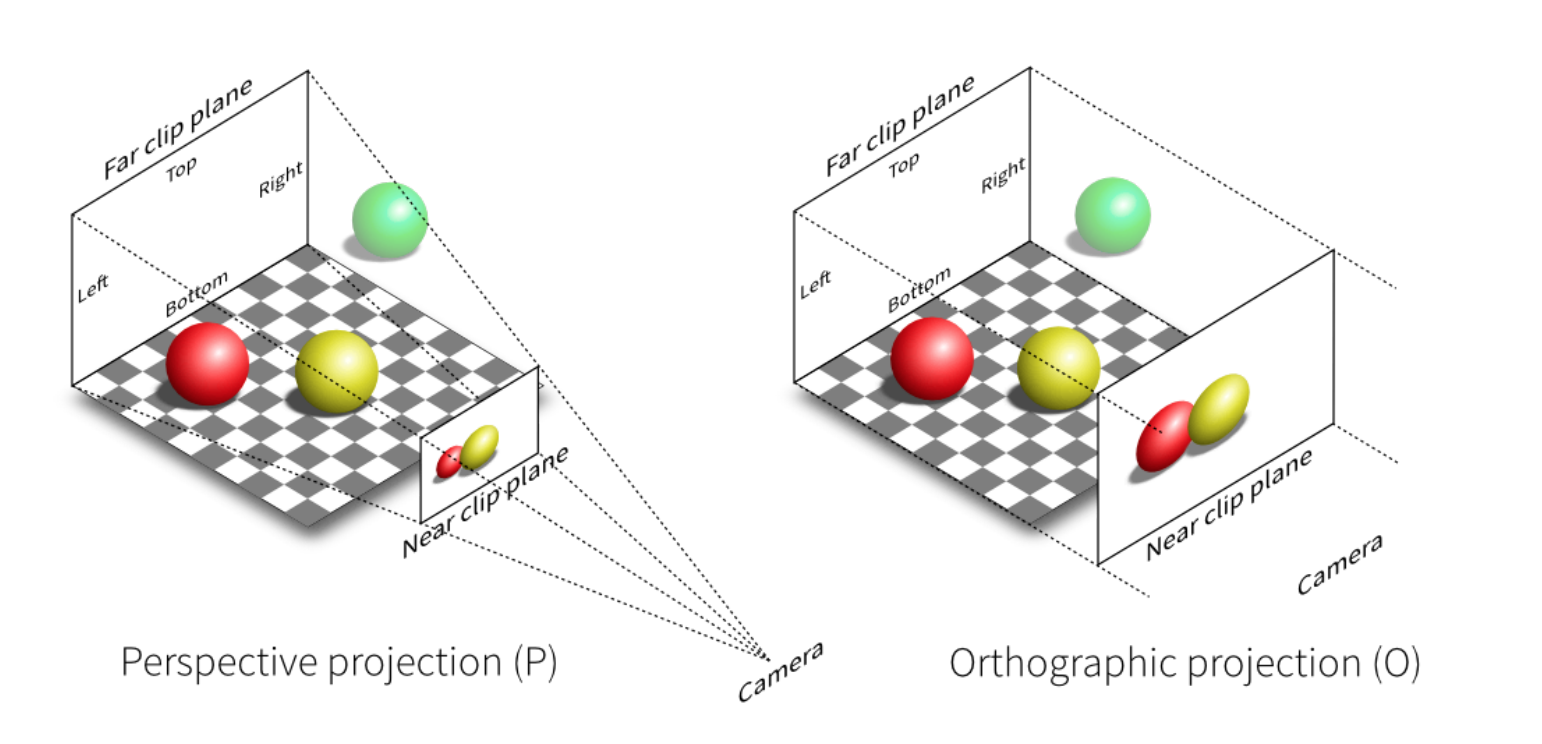
From perspective picture to orthographic picture
Orthographic Projection
例子理解
- Camera located at origin, looking at $-Z$, up at $Y$ .
- Drop $Z$ coordinate. 将$z$坐标去掉。
- Translate and scale the resulting rectangle to $[-1, 1]^2$.
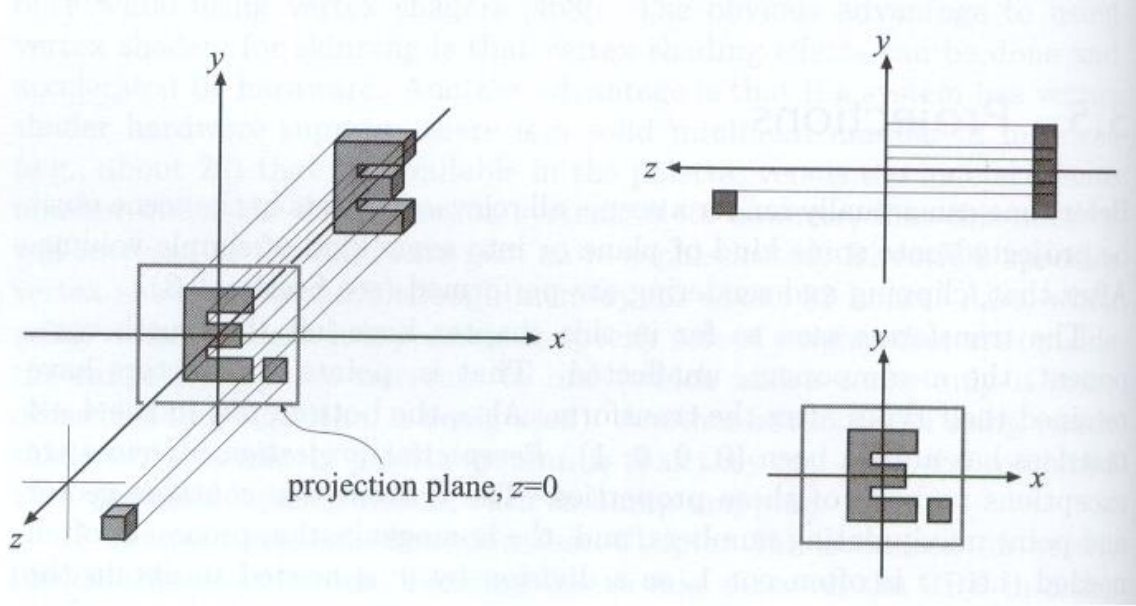
问题:如何区分前后,在去掉$z$坐标后?
真实操作
We want to map a cuboid $[l, r]\times [b, t]\times [f, n]$ to the “canonical (正则、规范、标准)” cube $[-1, 1]^3$.
- Center cuboid by translating.
- Scale into “canonical” cube.
Translate (center to origin) first, then scale (length/width/height to 2).
$$
M_{\text {ortho }}=
\left(\begin{array}{cccc}\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\left(\begin{array}{cccc}1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1\end{array}\right)
$$
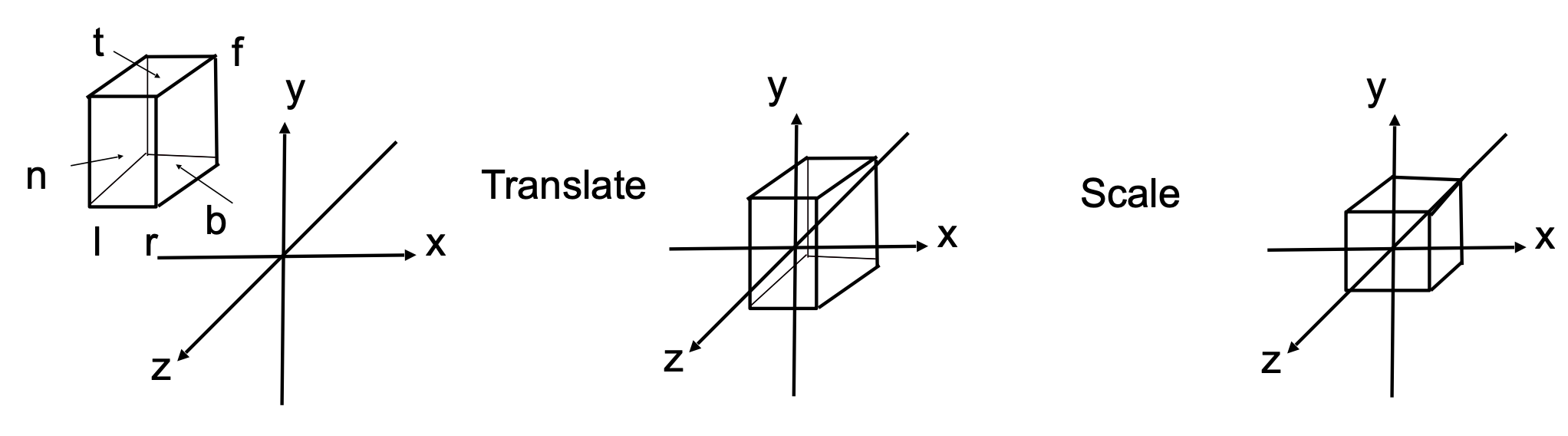
注意事项
- Looking at / along $-Z$ is making near and far not intuitive ($n > f$)
- That’s why OpenGL (a Graphics API) uses left hand coords.
问题
- 不考虑旋转?
- 变换到立方体中会造成拉伸?之后会有视口变换解决这个问题。
Perspective Projection
简介
- Most common in Computer Graphics, art, visual system
- Further objects are smaller
- Parallel lines not parallel; converge to single point
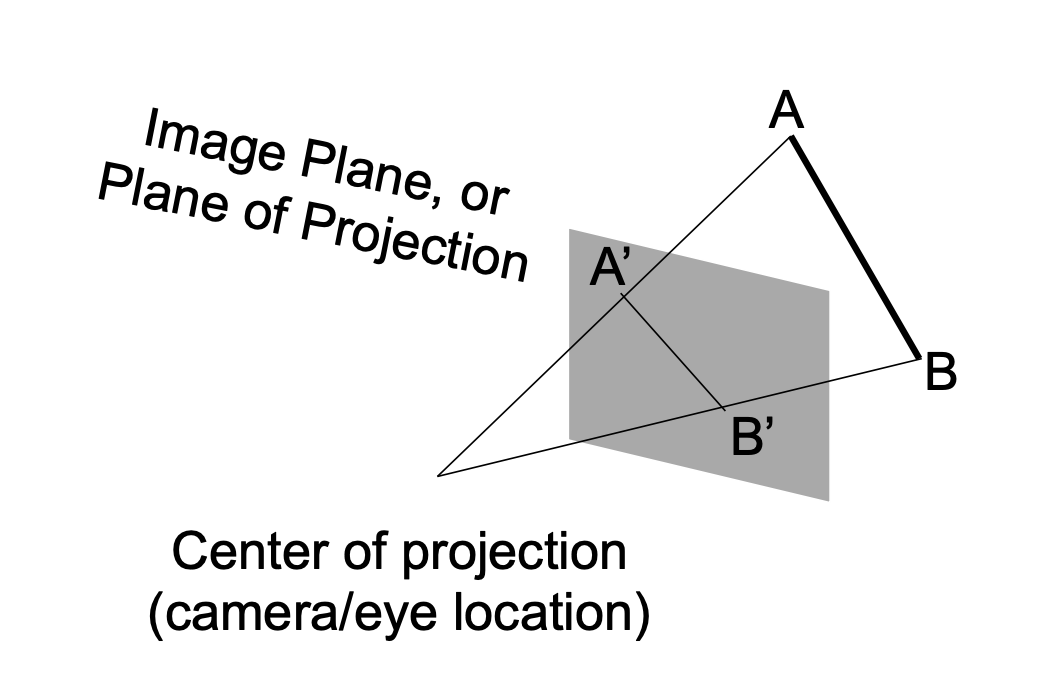
预备知识
- $(x, y, z, 1)$, $(kx, ky, kz, k \ne 0)$, $(xz, yz, z^2, z \ne 0)$ all represent
the same point $(x, y, z)$ in 3D - e.g. $(1, 0, 0, 1)$ and $(2, 0, 0, 2)$ both represent $(1, 0, 0)$
操作方法
- First “squish” the frustum into a cuboid: $n \rightarrow n, f \rightarrow f$, ($M_{persp \rightarrow ortho}$).
- Do orthographic projection: $M_{ortho}$ already known
在“挤压“的过程中,有几个原则需要遵守:
- 近平面 $n$ 上点的坐标不变;
- 远平面 $f$ 上的z坐标不变;
- 远平面 $f$ 上的中心点仍然是中心点;
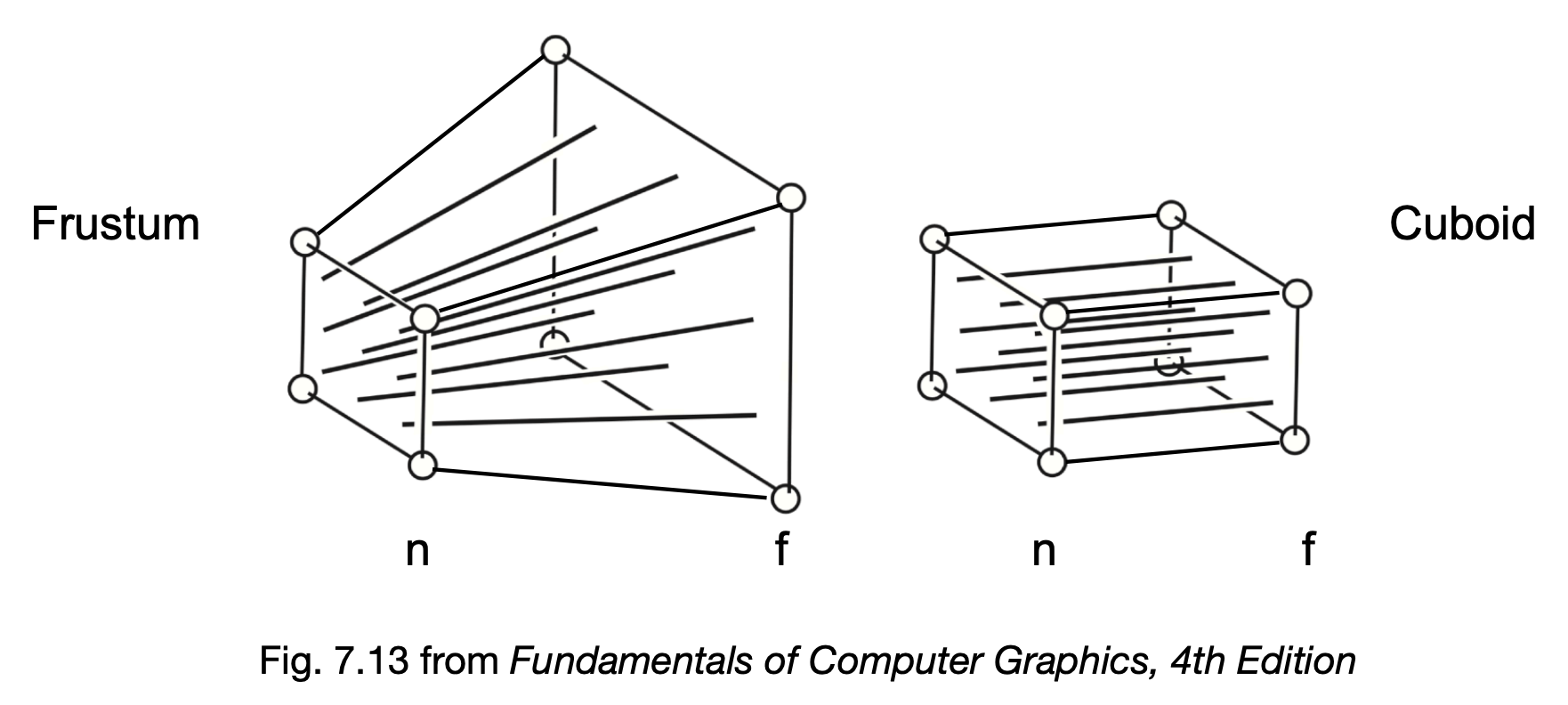
操作过程
Find the relationship between transformed points $(x^{\prime}, y^{\prime}, z^{\prime})$ and the original points $(x, y, z)$.
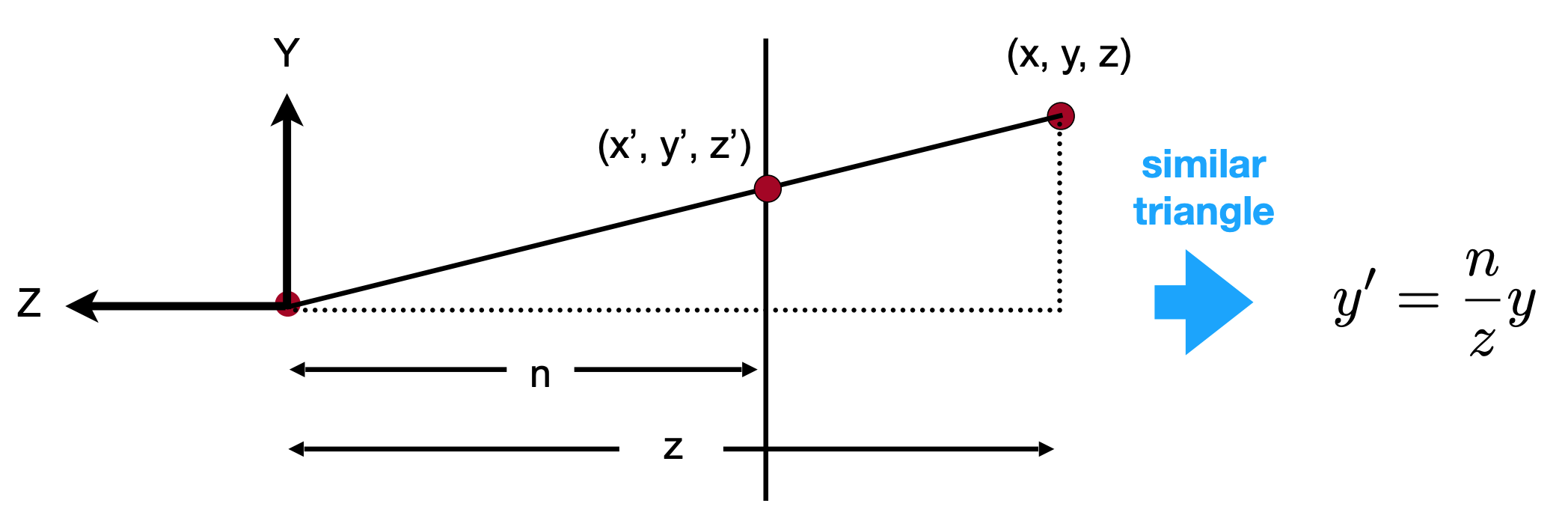
在图中,Z/Y交点为相机位置,即原点。$n$为近平面的z坐标,$z$为远平面对应z轴的坐标。
对应则有经过变换后,
$$
y^{\prime} = \frac{n}{z}y
$$
$$
x^{\prime} = \frac{n}{z}x
$$
对应到齐次坐标下:
$$
\left(\begin{array}{l}x \\
y \\
z \\
1
\end{array}\right)
\Rightarrow
\left(\begin{array}{c} nx/z \\
ny/z \\
\text{unknown} \\
1
\end{array}\right)
\overset{\times z}{==}
\left(
\begin{array}{c} nx \\
ny \\
\text{ still unknown } \\
z
\end{array}
\right)
$$
到此为止可以得到部分变换矩阵中的值:
$$
M_{persp \rightarrow ortho}^{4 \times 4}
\left(\begin{array}{l}x \\
y \\
z \\
1
\end{array}\right)
=
\left(
\begin{array}{c} nx \\
ny \\
\text{ still unknown } \\
z
\end{array}
\right)
$$
$$
M_{persp \rightarrow ortho}^{4 \times 4}
=
\mathbf{T}_{view} =
\left(\begin{array}{lll}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0
\end{array}\right)
$$
How to figure out the third row of $M_{persp \rightarrow ortho}$? The third row is responsible for $z^{\prime}$:
- Any point on the near plane will not change.
$$
\mathbf{M_{persp \rightarrow ortho}}^{4 \times 4}
\left(
\begin{array}{l} x \\
y \\
z \\
1
\end{array}\right)
=
\left(
\begin{array}{c} nx \\
ny \\
\text{unknown} \\
z
\end{array}
\right)
\overset{\text{replace z with n}}{\longrightarrow}
\left(\begin{array}{l}x \\
y \\
n \\
1
\end{array}\right)
\Rightarrow
\left(\begin{array}{l}x \\
y \\
n \\
1
\end{array}\right)==
\left(\begin{array}{l} nx \\
ny \\
n^{2} \\
n
\end{array}\right)
$$
所以得到:the third row must be of the form $(0 \ 0 \ A \ B)$, $n^2$ has nothing to do with $x$ and $y$.
$$
\left(\begin{array}{lll}0 & 0 & A\end{array}\right. B)\left(\begin{array}{l}x \ y \ n \ 1\end{array}\right)=n^{2}
$$
$$
An + B = n^2
$$
- Any point’s z on the far plane will not change:这里取远平面的中心点。
$$
\left(\begin{array}{l}0 \\
0 \\
f \\
1
\end{array}\right)
\Rightarrow
\left(\begin{array}{l}0 \\
0 \\
f \\
1
\end{array}\right)
==
\left(\begin{array}{c}0 \\
0 \\
f^{2} \\
f\end{array}\right)
$$
$$
Af + B = f^2
$$
综合上述两者,
$$
\begin{array}{ll}
An+B=n^{2} \\
Af+B=f^{2}
\end{array}
\Rightarrow
\begin{array}{ll}
A=n+f \\
B=-nf
\end{array}
$$
之后做orthographic projection即可:
$$
M_{persp} = M_{ortho} M_{persp \rightarrow ortho}
$$
透视投影中Frustum的另一种表示
当得到近平面的坐标信息后,有时人们用另外一种方式表示Frustum视锥。
People prefer: vertical field-of-view (fovY) and aspect ratio (assume symmetry $l = -r, b = -t$).
该表示方法可以与cuboid中的 $l,r,b,t,n,f$ 相转化。
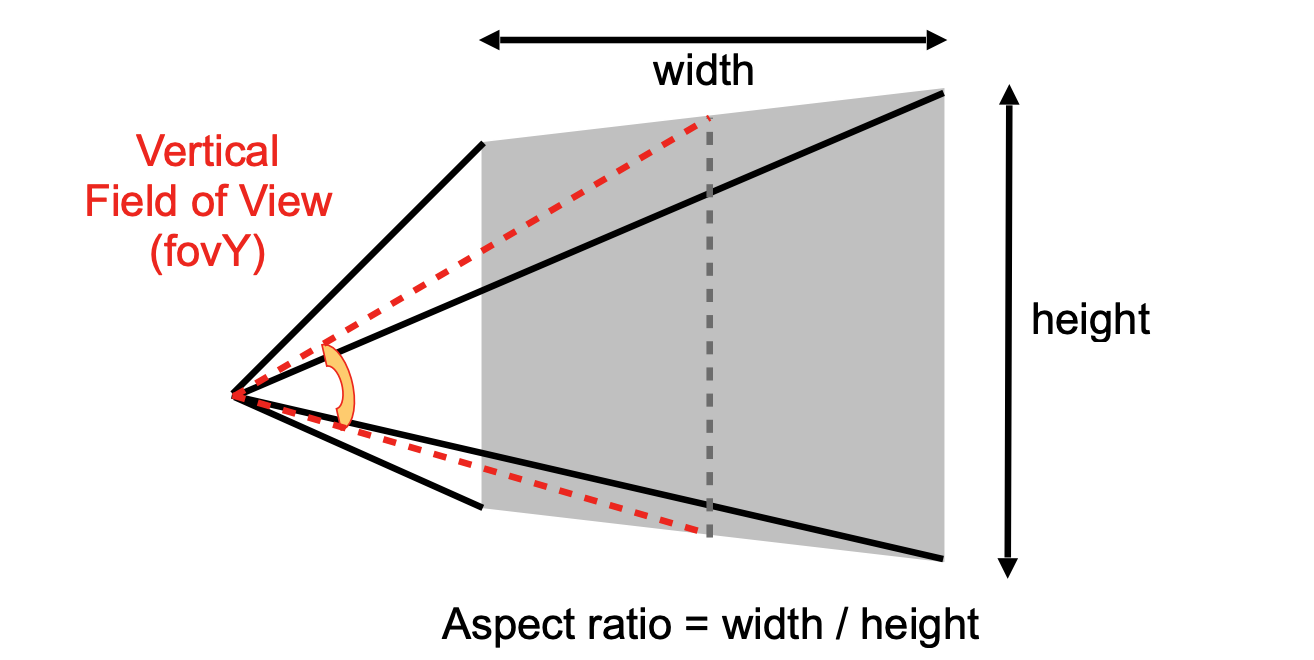
注意:上述平面只是frustum的近平面。
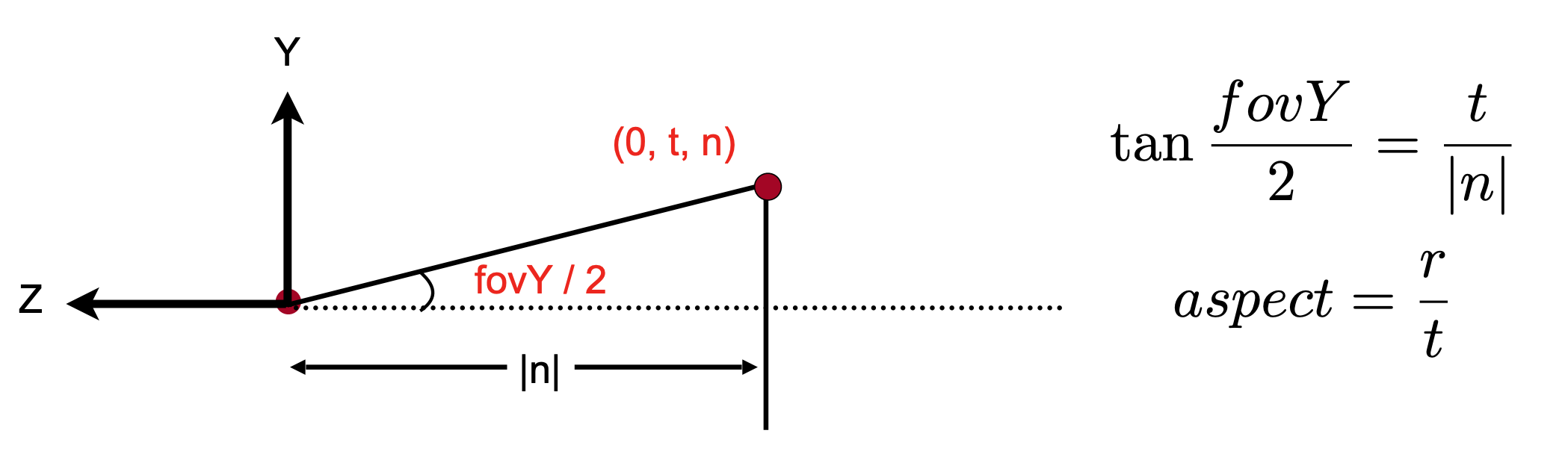
思考问题
对于任意一个frustum内部的点,经过透视投影映射到cuboid, 其 $z$ 坐标相对于之前有什么变化?
$$
\mathbf{M}_{persp \rightarrow ortho} =
\left(\begin{array}{lll}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right)
$$
对于任意一点经过该变换可得:
$$
\mathbf{M}_{persp \rightarrow ortho}
\left(
\begin{array}{l}x \\
y \\
z \\
1
\end{array}\right)
=
\left(
\begin{array}{c} nx \\
ny \\
(n+f)z - nf \\
z
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{c} nx/z \\
ny/z \\
(n+f) - nf/z \\
1
\end{array}
\right)
$$
为了判断 $z$ 坐标的变化,定义函数 $f(z)$:
$$
\begin{aligned}
f(z) &= \frac{(n+f)z - nf}{z} - z \\
& \overset{\times z}{=} -z^2 + (n+f)z -nf \\
&= (z-n)(f-z)
\end{aligned}
$$
由于:$f \le z \le n$,因此$f(z) \ge 0$,因此得到在乘以 $z$ 坐标之前的 $f(z) \le 0$,因为看向的是-z方向,因此 $z$ 坐标均为负数。由此得到,当完成“挤压”后,frustum内部的点均向远平面方向移动,即离相机更远了。

