GAMES101-05：Rasterization - Triangles

Viewing之后

• Model transformation (placing objects)
• View transformation (placing camera)
• Projection transformation
  • Orthographic projection (cuboid to “canonical” cube $[-1, 1]^3$)
  • Perspective projection (frustum to “canonical” cube)
• Canonical cube to?

继续：将之前得到的立方体绘制到屏幕上。

Canonical Cube to Screen

概念定义

• What is a screen
  • An array of pixels
  • Size of the array: resolution 表示像素的多少。
  • A typical kind of raster display
• Raster == screen in German
  • Rasterize == drawing onto the screen
• Pixel (FYI, short for “picture element”)
  • For now: A pixel is a little square with uniform color 简化表示
  • Color is a mixture of (red, green, blue)

Screen space

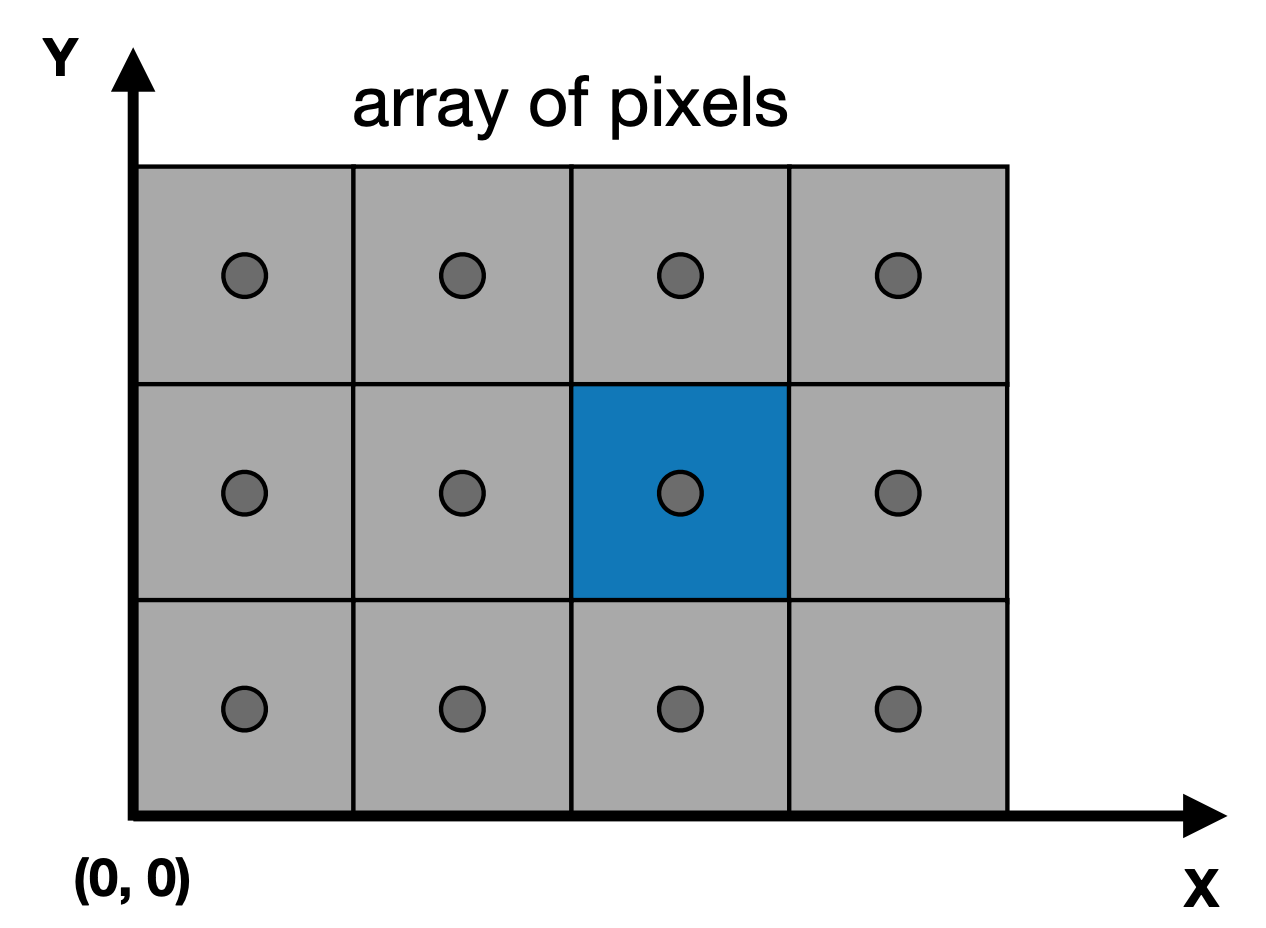
规则：

• Pixels’ indices are in the form of $(x, y)$, where both x and y are integers.
• Pixels’ indices are from $(0, 0)$ to (width - 1, height - 1).
• Pixel $(x, y)$ is centered at $(x + 0.5, y + 0.5)$ . 坐标实际中心
• The screen covers range $(0, 0)$ to (width, height).

操作方法

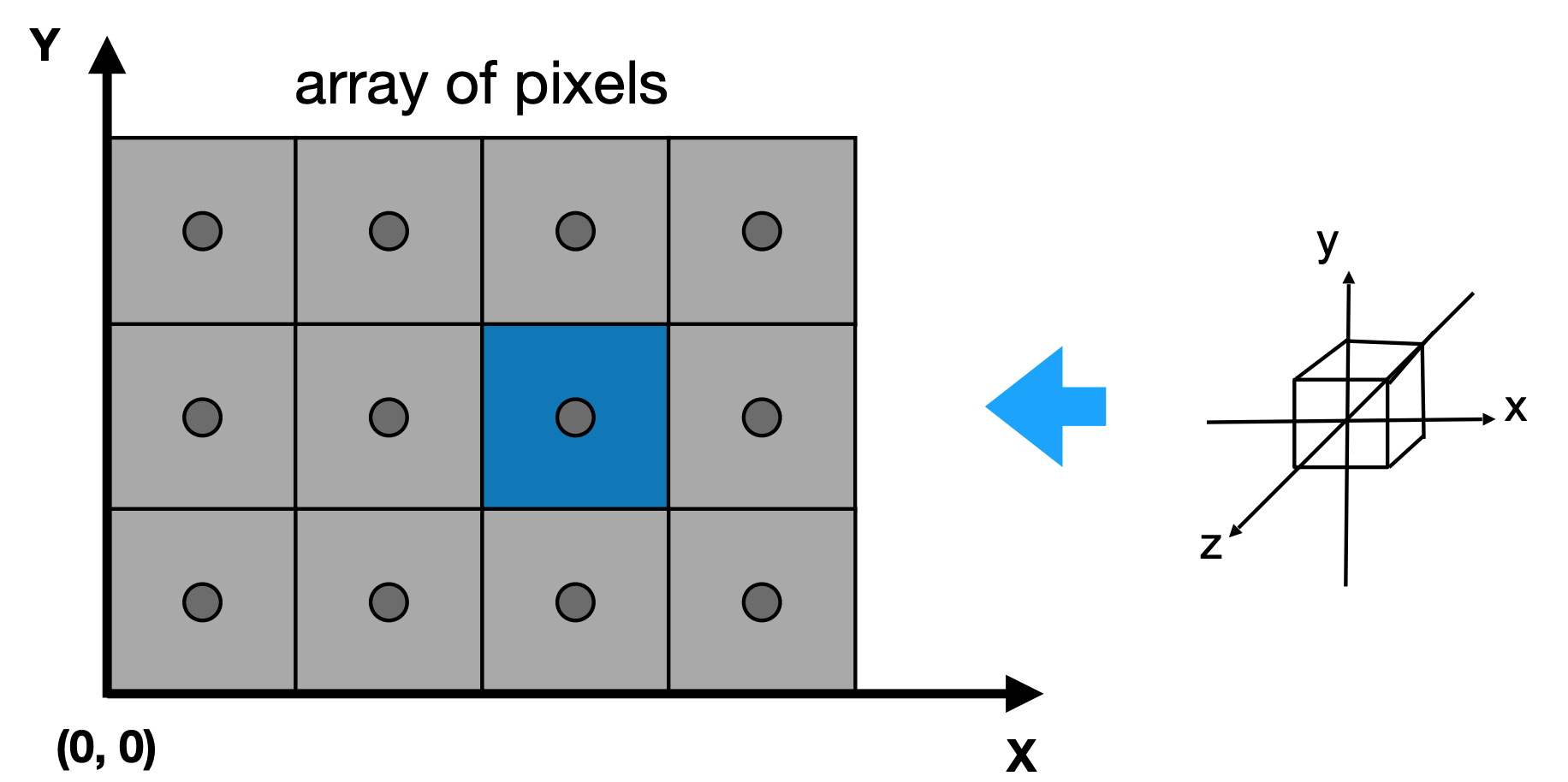
• Irrelevant to z
• Transform in xy plane: $[-1, 1]^2$ to [0, width] x [0, height]
• Viewport transform matrix: 视口变换

$$
M_{\text {viewport}}=\left(\begin{array}{cccc}\frac{w i d t h}{2} & 0 & 0 & \frac{\text { width }}{2} \\
0 & \frac{\text { height }}{2} & 0 & \frac{\text { height }}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
$$

到此为止得到了2D上的图片。

Rasterizing Triangles into Pixels

接下来，将图片分解为像素，也就是光栅化的过程。

Drawing Machines

• CNC Sharpie Drawing Machine
• Laser Cutters

Different Raster Displays

• Oscilloscope 示波器
• Cathode Ray Tube 阴极射线管
  • Television - Raster Display CRT
• Frame Buffer: Memory for a Raster Display
• Flat Panel Displays
  • LCD (Liquid Crystal Display)
  • LED Array Display
• Electrophoretic (Electronic Ink) Display

Rasterization: Drawing to Raster Displays

Triangles - Fundamental Shape Primitives

Why triangles?

• Most basic polygon
  • Break up other polygons
• Unique properties
  • Guaranteed to be planar 三角形一定是平面图形
  • Well-defined interior 内外容易区分
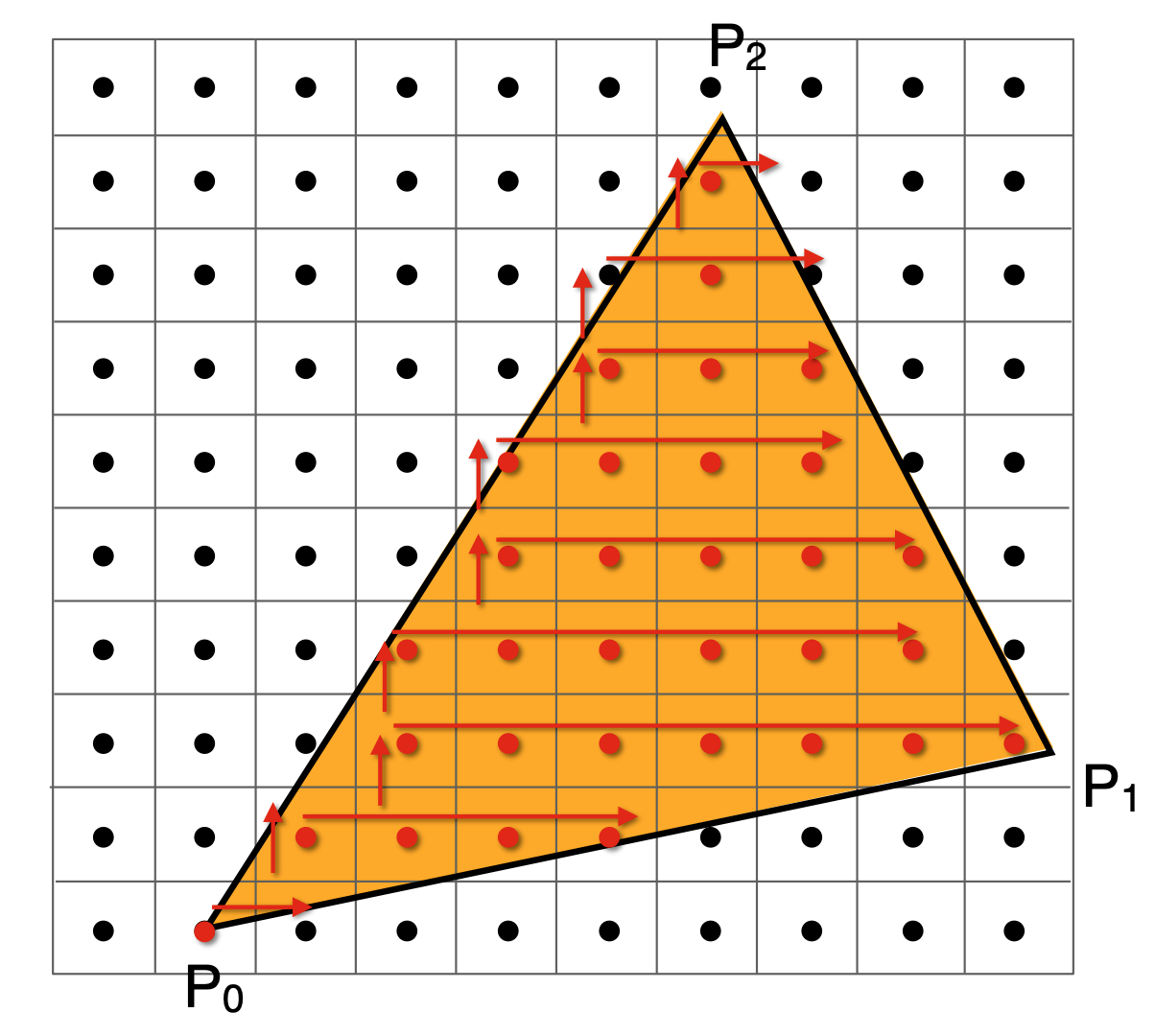
  • Well-defined method for interpolating values at vertices over triangle (barycentric interpolation) 根据顶点的信息可以对其中其中任意一点进行插值。

问题：What Pixel Values Approximate a Triangle?

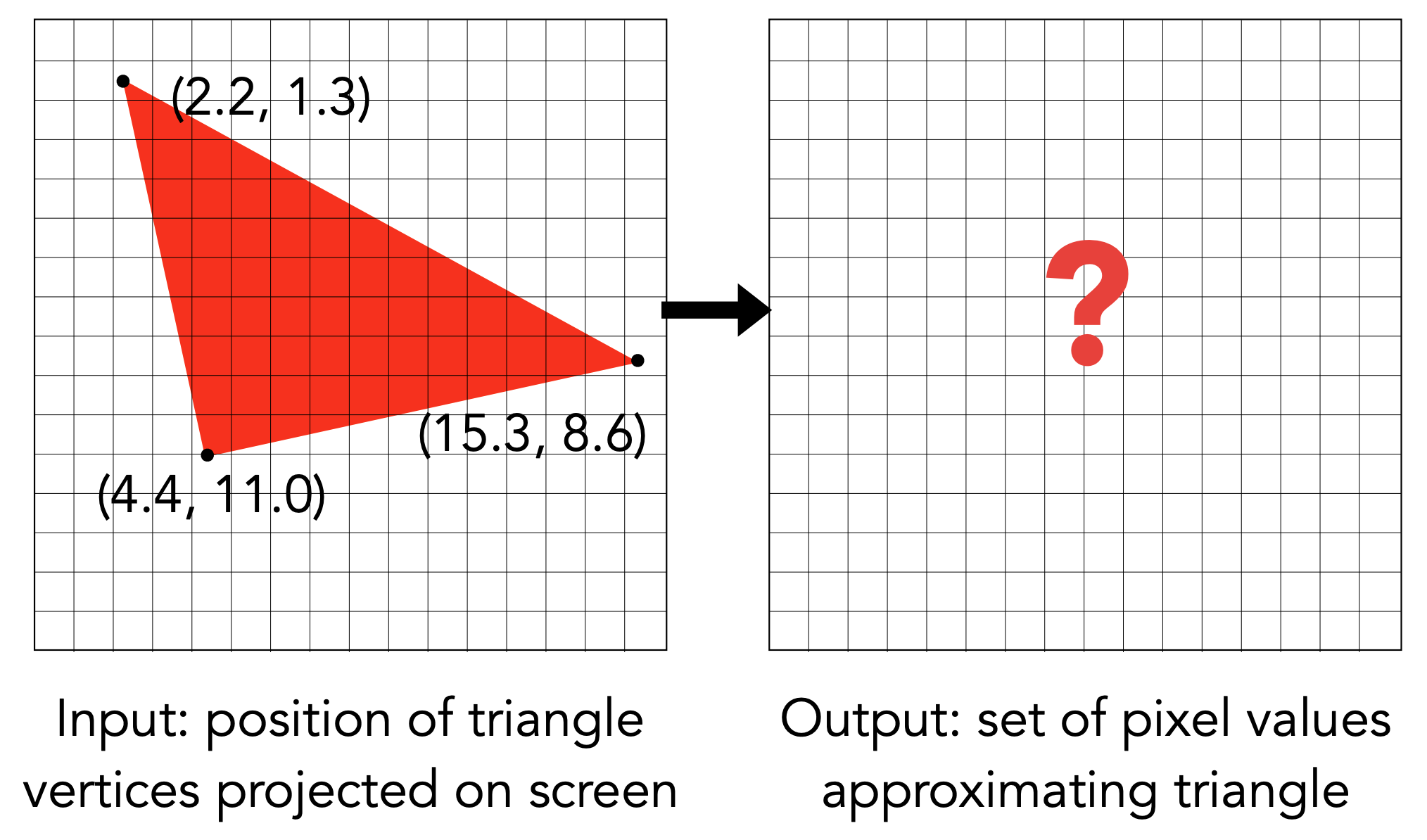
解决方法：Sampling

含义

• Evaluating a function at a point is sampling.
• We can discretize a function by sampling.

  for (int x = 0; x < xmax; ++x)
      output[x] = f(x);
  

• Sampling is a core idea in graphics.
  • We sample time (1D), area (2D), direction (2D), volume (3D)

具体过程

• Sample If Each Pixel Center Is Inside Triangle
• Define Binary Function: $\text{inside}(t, x, y)$
  • x, y: not necessarily integers

$$
\text{inside}(t, x, y)=
\left\{
\begin{array}{ll}
1 & \begin{array}{l} \text{Point (x, y) in triangle } t\end{array} \\
0 & \text {otherwise}
\end{array}
\right.
$$

整体过程表示如下：

for (int x = 0; x < xmax; ++x)
    for (int y = 0; y < ymax; ++y)
        image[x][y] = inside(tri, x + 0.5, y + 0.5);

上述过程中要解决的一个问题是：如何判断点 $(x,y)$ 在三角形内。使用之前cross product中提到的方法。

最后的结果：

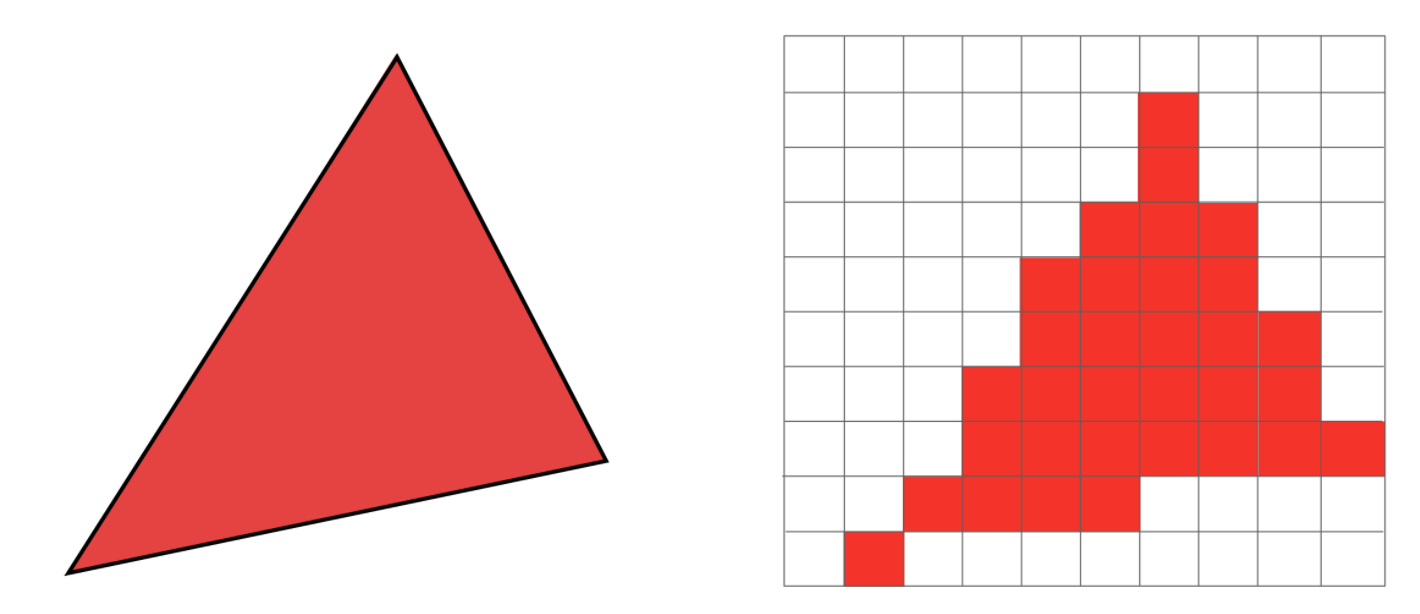
存在锯齿问题！

Edge Cases

Is this sample point covered by triangle 1, triangle 2, or both? 自己决定，不作要求。

优化策略

• 普遍策略：Checking All Pixels on the Screen? Use a Bounding Box!

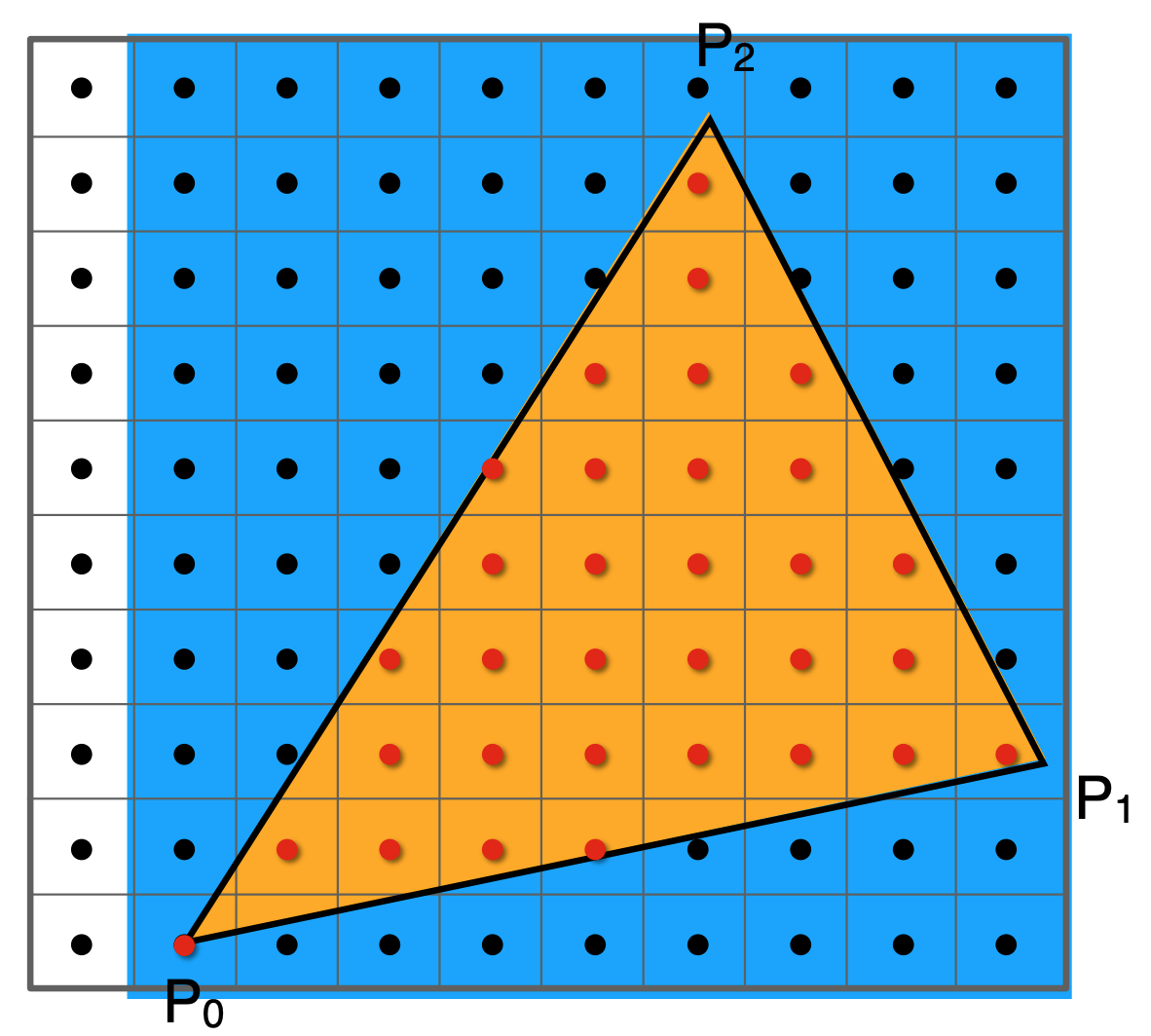
• 进一步优化：Incremental Triangle Traversal，每一行都找边界，suitable for thin and rotated triangles，但是实践起来不太容易。