Sampling
常见的采样
- Rasterization = Sample 2D Positions
- Photograph = Sample Image Sensor Plane
- Video = Sample Time
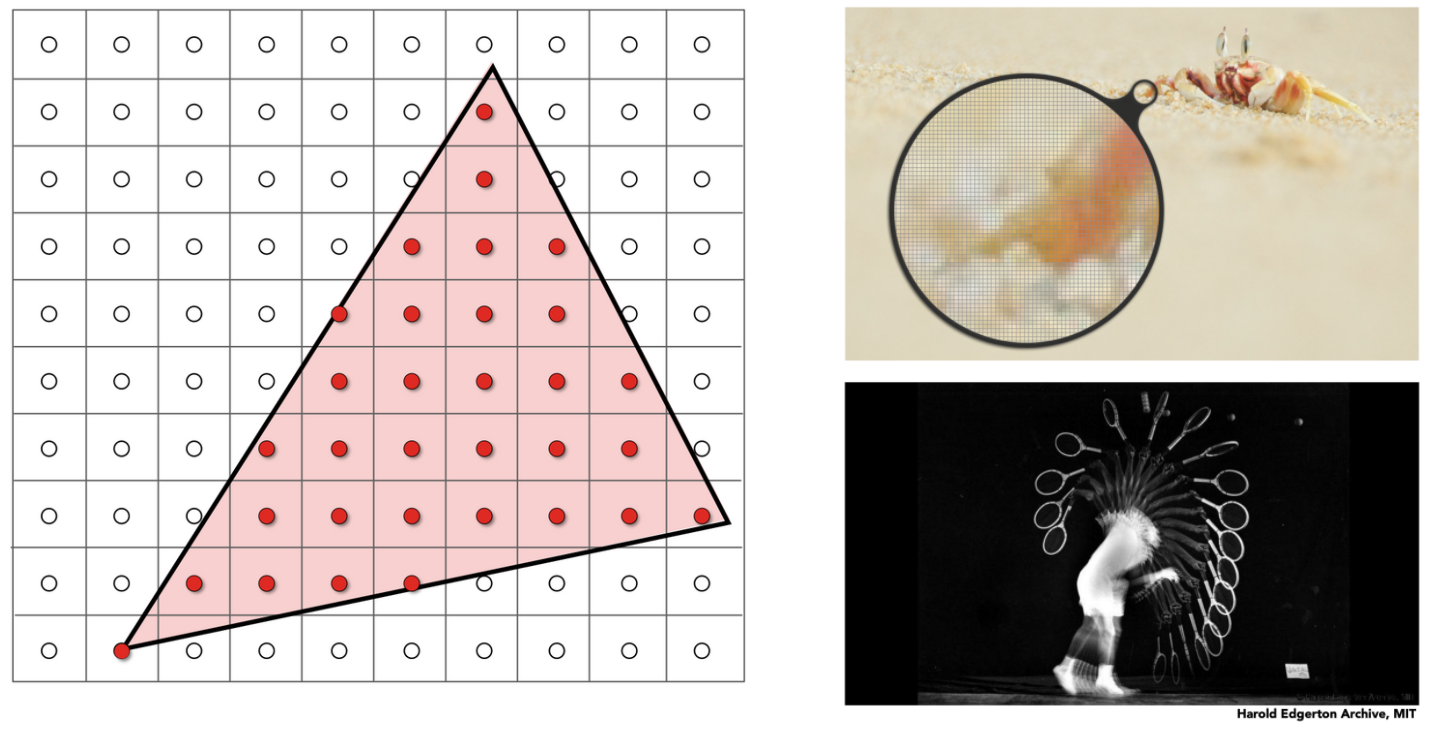
采样会产生问题——Aliasing
Sampling Artifacts (Errors / Mistakes / Inaccuracies) in Computer Graphics：
- Jaggies (Staircase Pattern)：This is also an example of “aliasing” – a sampling error；
- Moiré Patterns in Imaging：Skip odd rows and columns
- Wagon Wheel Illusion (False Motion)：人眼对时间的采样无法跟上运动的速度。
Behind the Aliasing Artifacts: Signals are changing too fast (high frequency), but sampled too slowly.
如何Antialiasing
Idea
Blurring (Pre-Filtering) Before Sampling. 采样之前进行模糊（滤波）。
例子
在Rasterization的过程中，反走样方法的效果：
- 只采样：Note jaggies in rasterized triangle where pixel values are pure red or white;
- 模糊再采样：Note antialiased edges in rasterized triangle where pixel values take intermediate values;
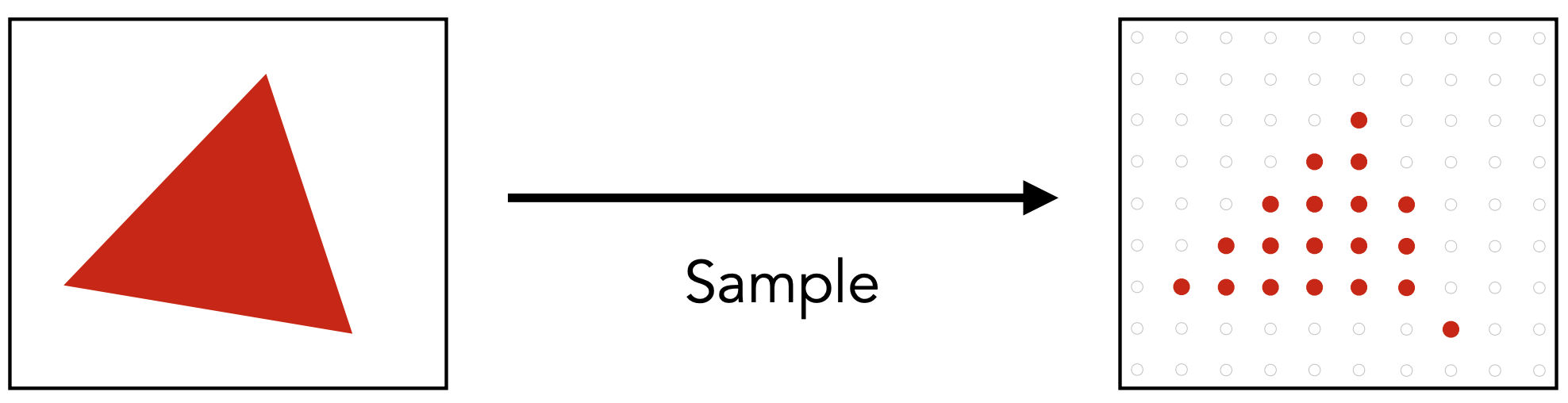
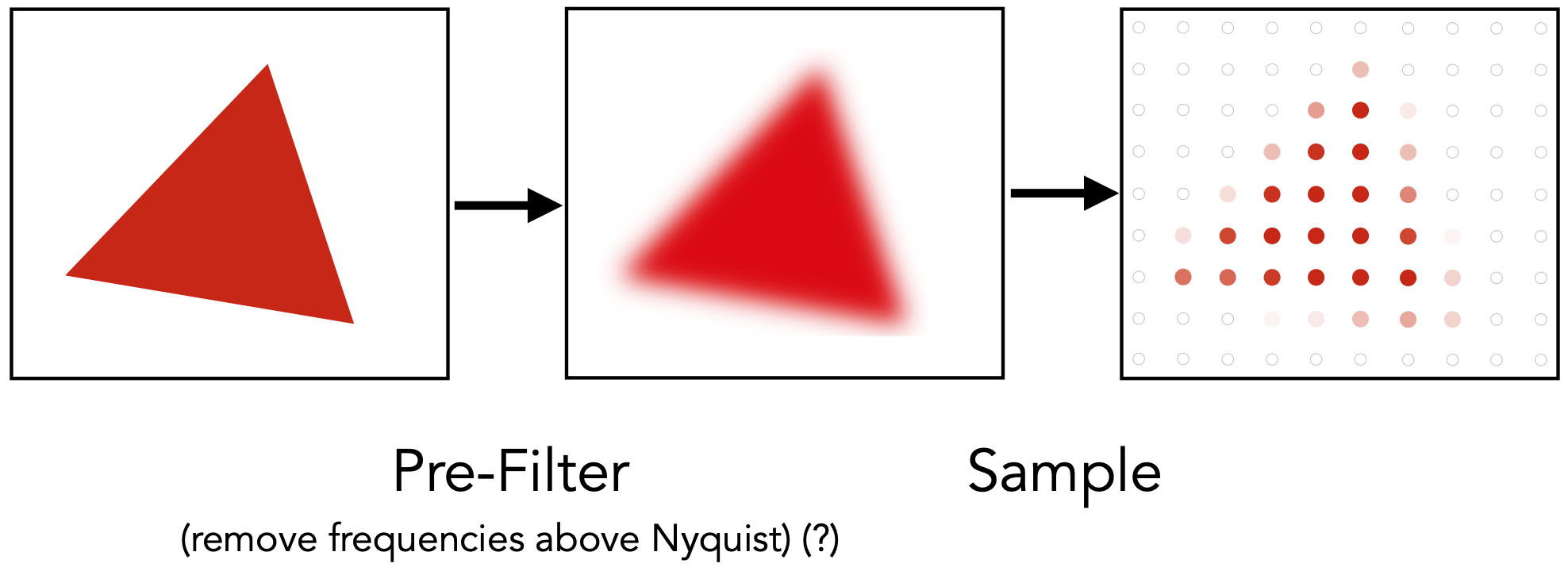
Blurred Aliasing: 先采样再模糊行吗？
不可以，下图中左上是原始图形，右上和右下均为先模糊再采样，左下则为先采样再模糊，发现仍然有走样现象。
问题
- Why undersampling introduces aliasing?
- Why pre-filtering then sampling can do antialiasing?
Fourier Transform
频率
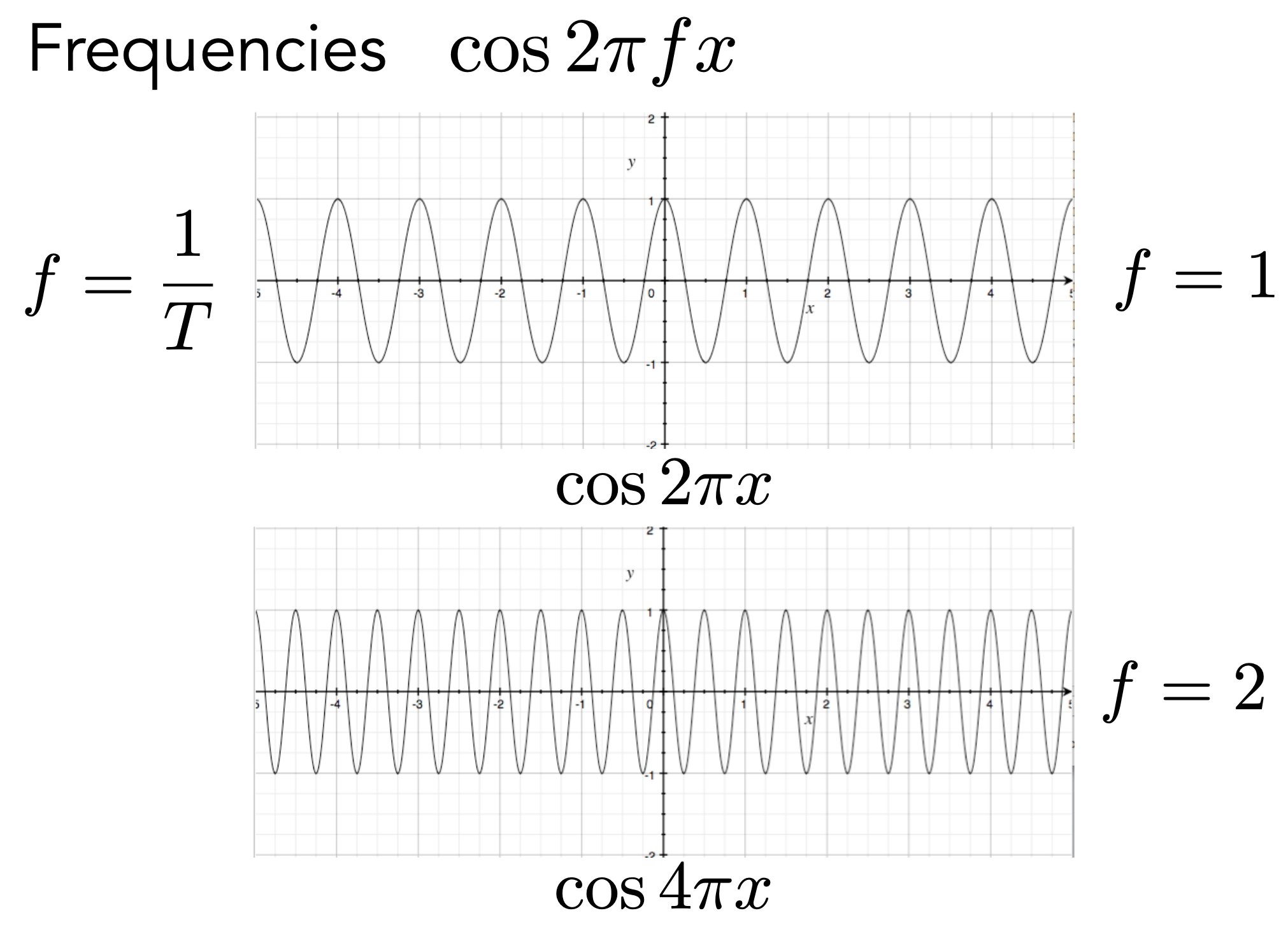
含义
Represent a function as a weighted sum of sines and cosines.
注意：这里的函数不一定是传统的周期函数，也可以是非周期函数，只是将非周期函数的周期视为无穷大而已。
作用
Fourier Transform Decomposes A Signal Into Frequencies.
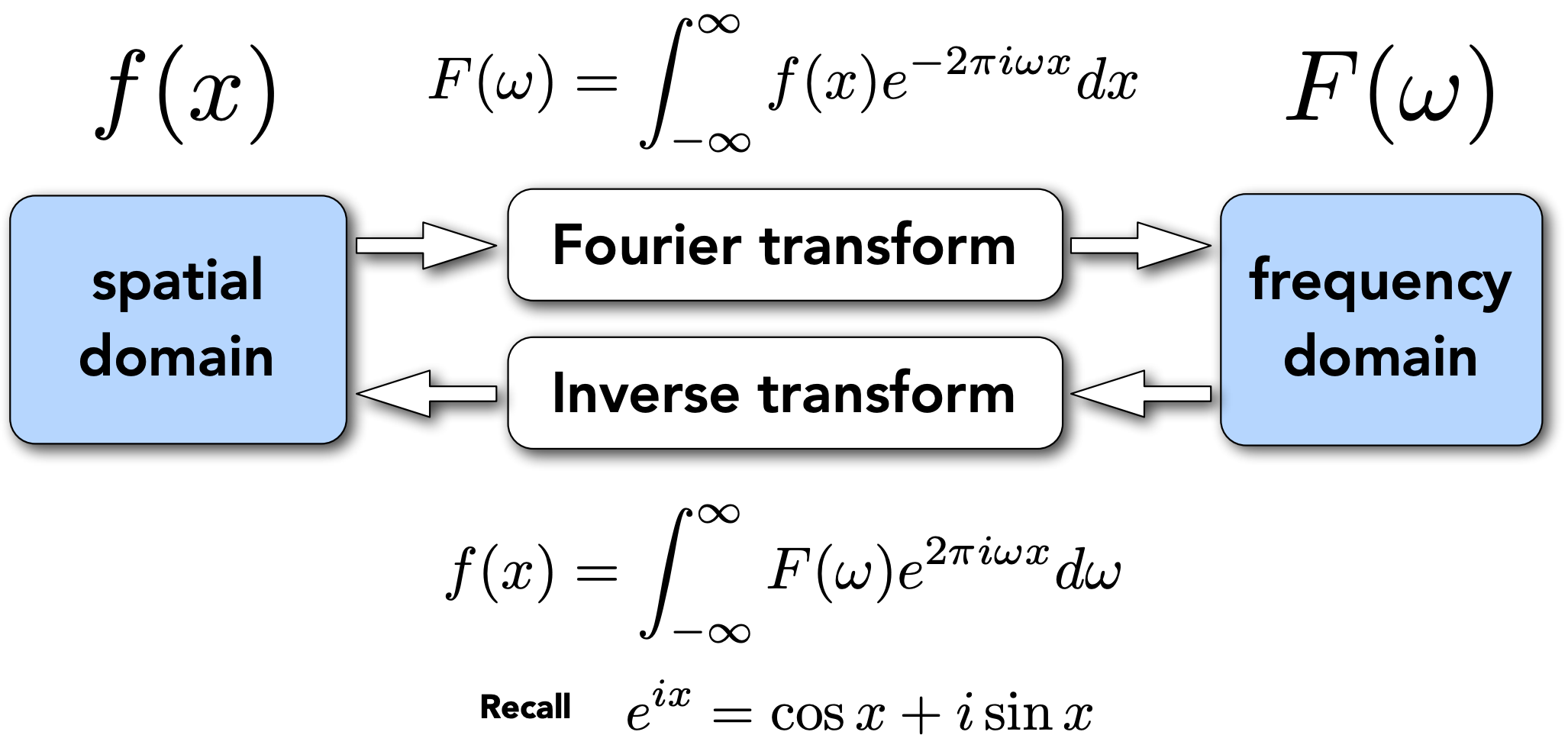
解释Aliasing
Higher Frequencies Need Faster Sampling
- 对低频信号的采样，采样率与信号频率相差不多，也能够大致重建原始信号；
- 对高频信号的采样，当采样率过低时，重建原始信号时会出现错误；
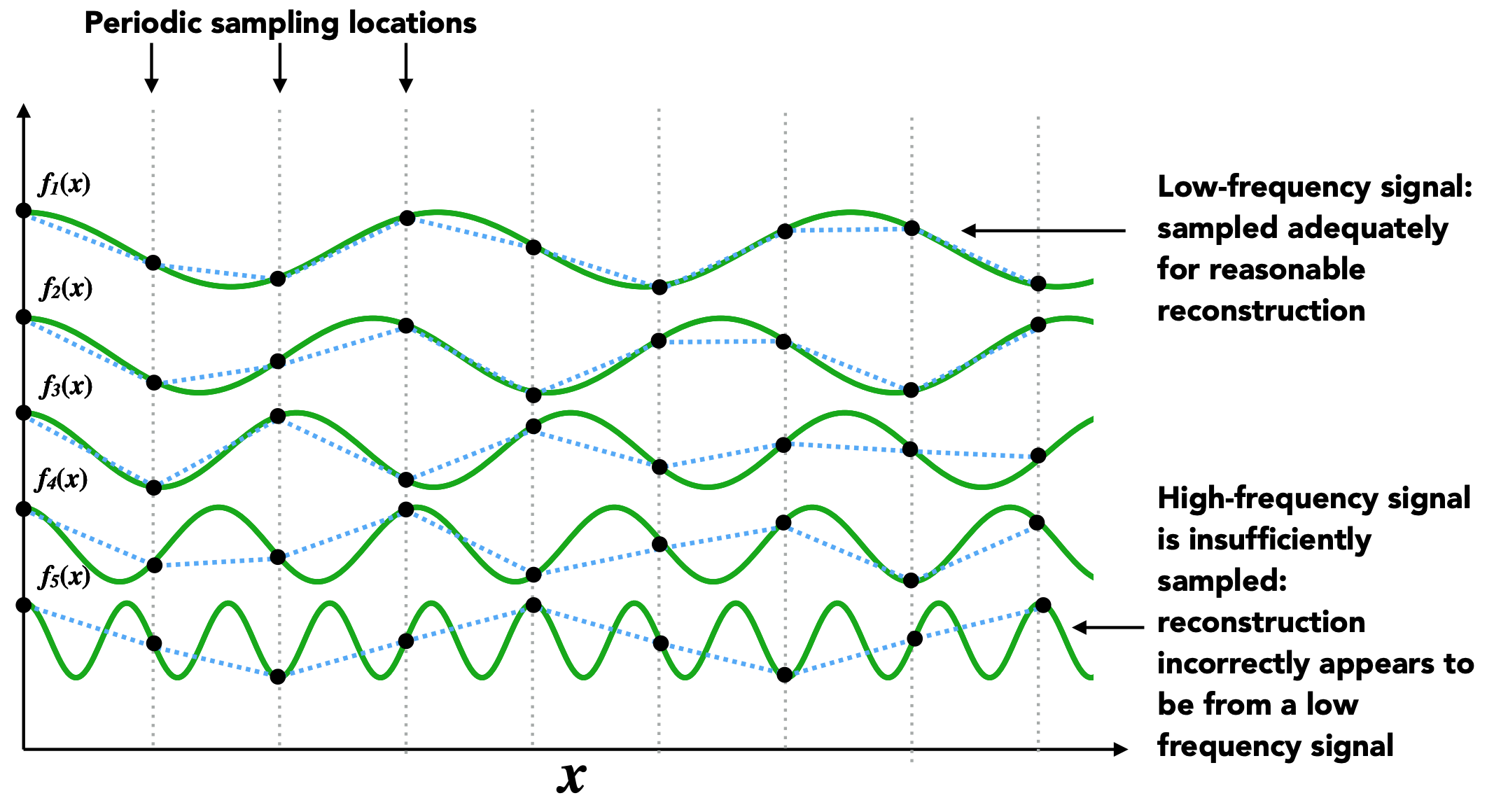
Undersampling Creates Frequency Aliases
使用同样的采样率对两个不同频率的函数采样，发现得到的结果相同，也就是说，利用该采样得到的结果重建信号时，无法区分原始信号是哪个。
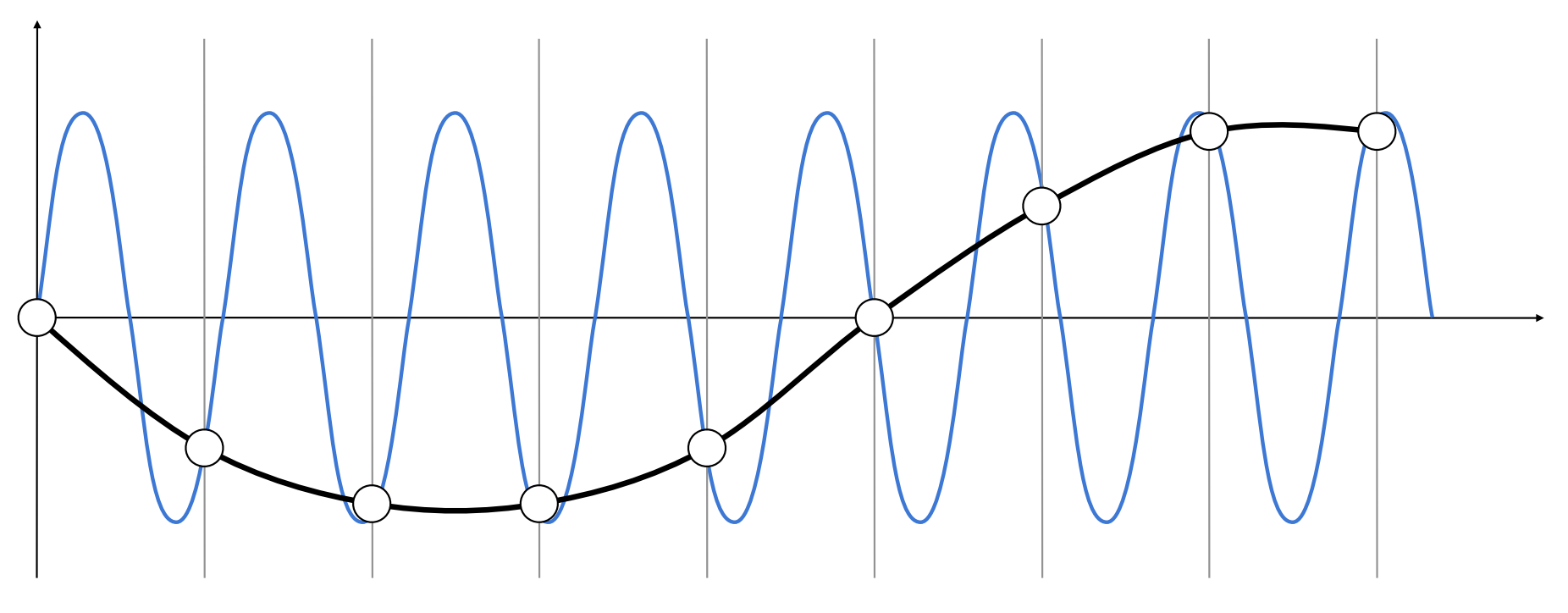
- High-frequency signal is insufficiently sampled: samples erroneously appear to be from a low-frequency signal
- Two frequencies that are indistinguishable at a given sampling rate are called “aliases”
Filtering
介绍
Filtering = Getting rid of certain frequency contents.
傅里叶变换的频域信息如何理解？
- 中心是最低频，周围是高频内容；
- 频域的信息通过通过右图中的亮度表示，信息越多，则越亮；
- 图中每一点的灰度值描述的是正弦或者余弦函数的振幅；
- 中间有两个交叉的亮十字如何理解？
- 因为将分析的信号视为周期重复性信号，但是对于不重复的信号，例如图片，则将其视为水平方向重复很多，竖直方向也重复很多；
Filtering可得到特定频域信息
- High-pass filter
- Low-pass filter
- Filter Out Low and High Frequencies
Filtering = Convolution (= Averaging)
Convolution
Point-wise local averaging in a “sliding window”.
这里的操作与数学上的定义不同，如果严格按照数学定义需要旋转卷积核。
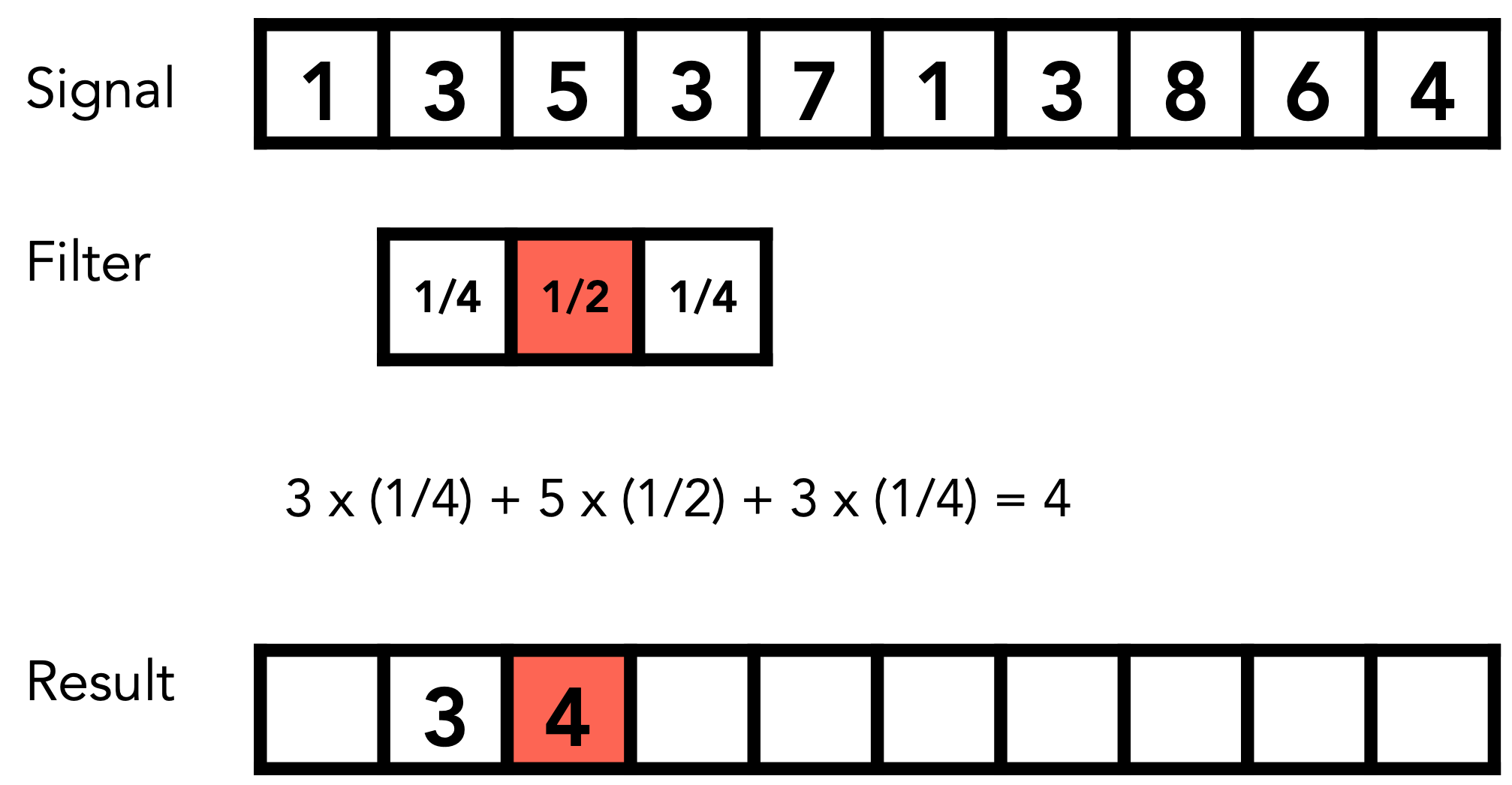
Convolution Theorem
Convolution in the spatial domain is equal to multiplication in the frequency domain, and vice versa.
根据卷积定理，以下两种操作是等价的：
- Option 1
- Filter by convolution in the spatial domain
- Option 2
- Transform to frequency domain (Fourier transform)
- Multiply by Fourier transform of convolution kernel
- Transform back to spatial domain (inverse Fourier)
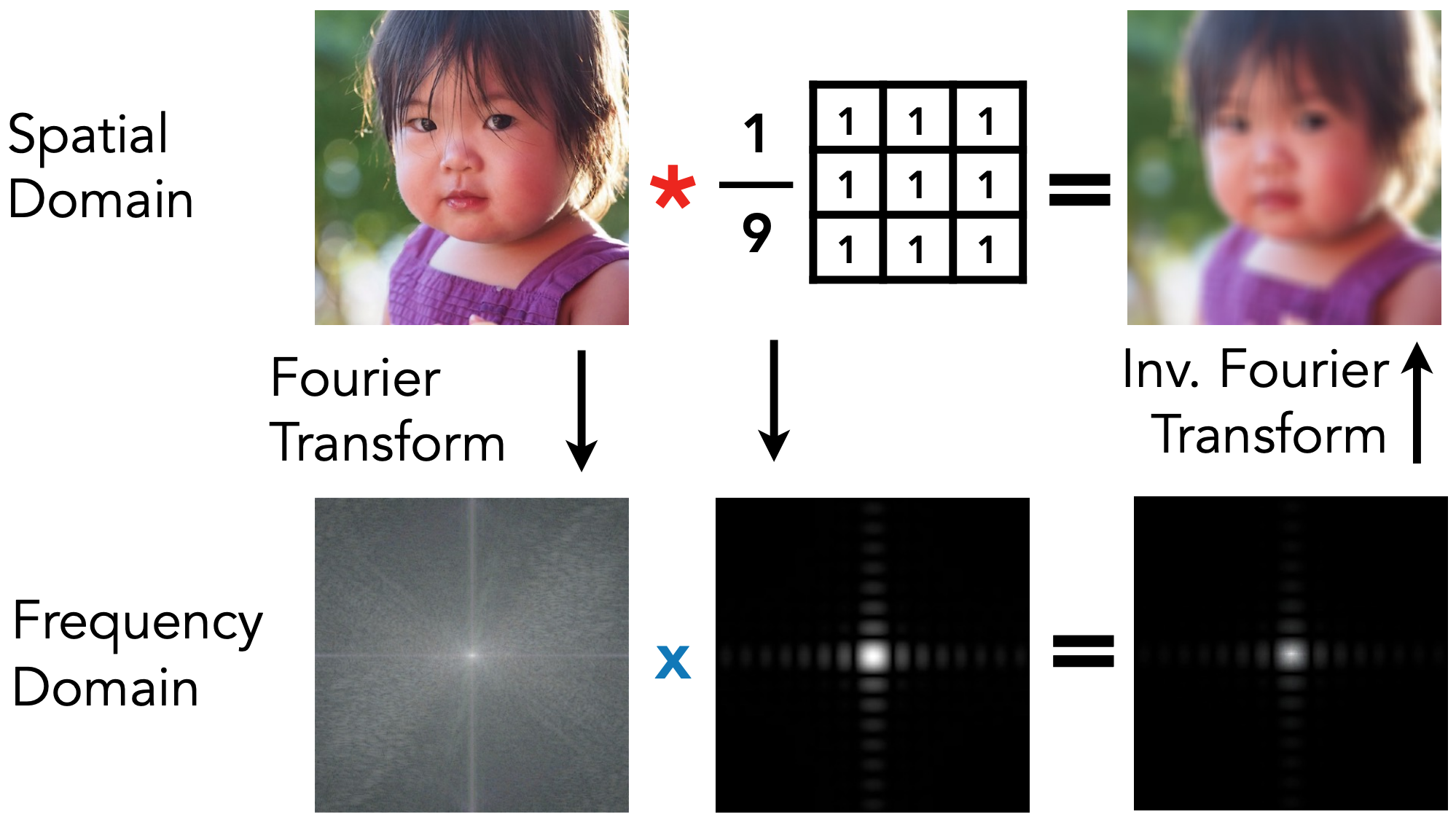
Box Filter
$$
\frac{1}{9}
\left(
\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}
\right)
$$
归一化操作是为了不会影响亮度的剧烈变化。
- Box Function = “Low Pass” Filter 左侧是时域信息，右侧是频域信息。
- Wider Filter Kernel = Lower Frequencies
理解方式：当卷积核变大，说明移动的窗口覆盖的范围变大，因为有更多的区域被“平滑”了，因此高频信息都消失了。从极端的角度理解，当卷积核与图像相同时，整个图像都被“平滑”了，对应到频域信息中的区域会更小。当卷积核的大小与一个像素相同时，说明图像没有被“平滑”，因此频域信息不变。
回顾Sampling
Sampling=Repeating Frequency Contents
例子
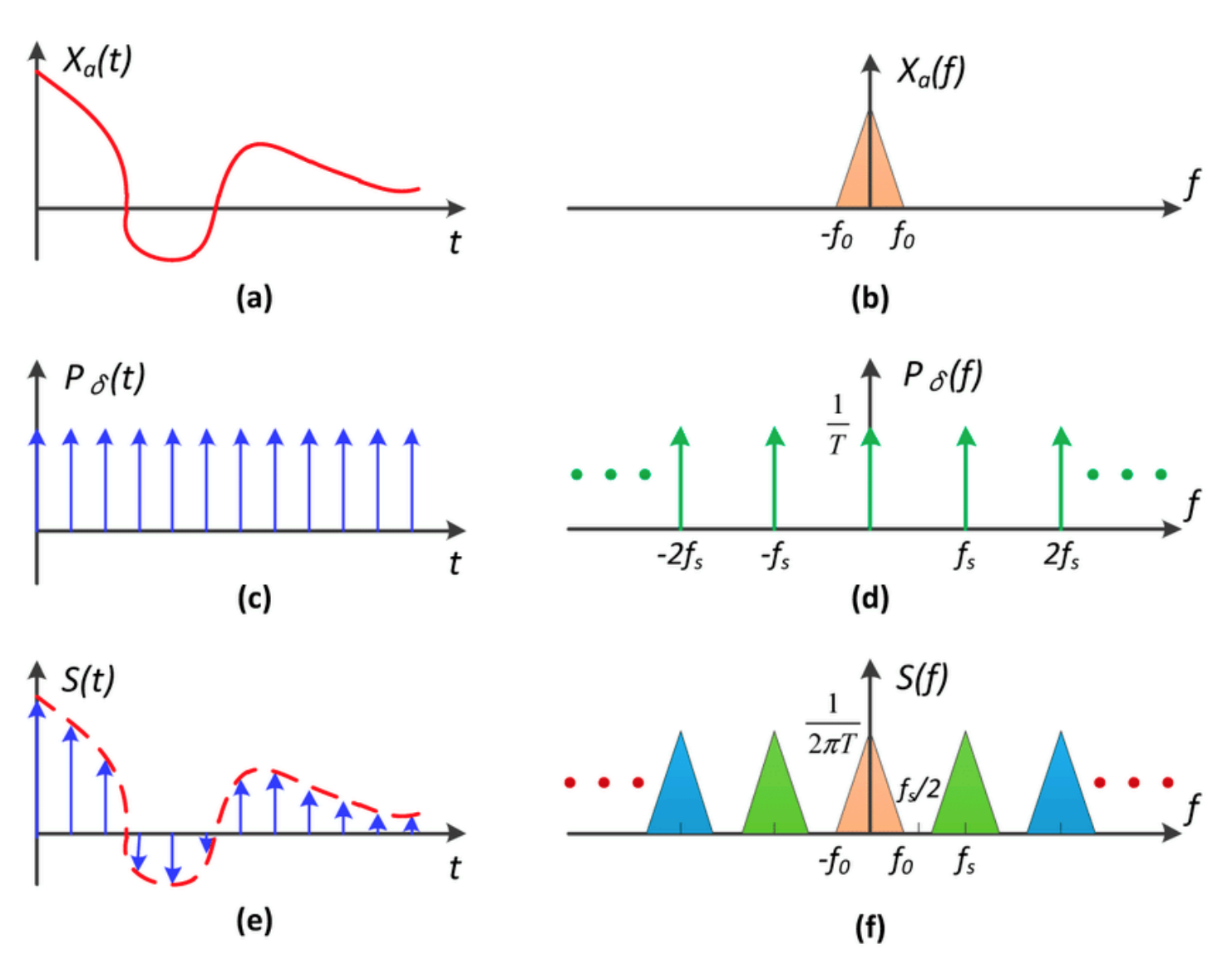
解释Aliasing
Aliasing = Mixed Frequency Contents
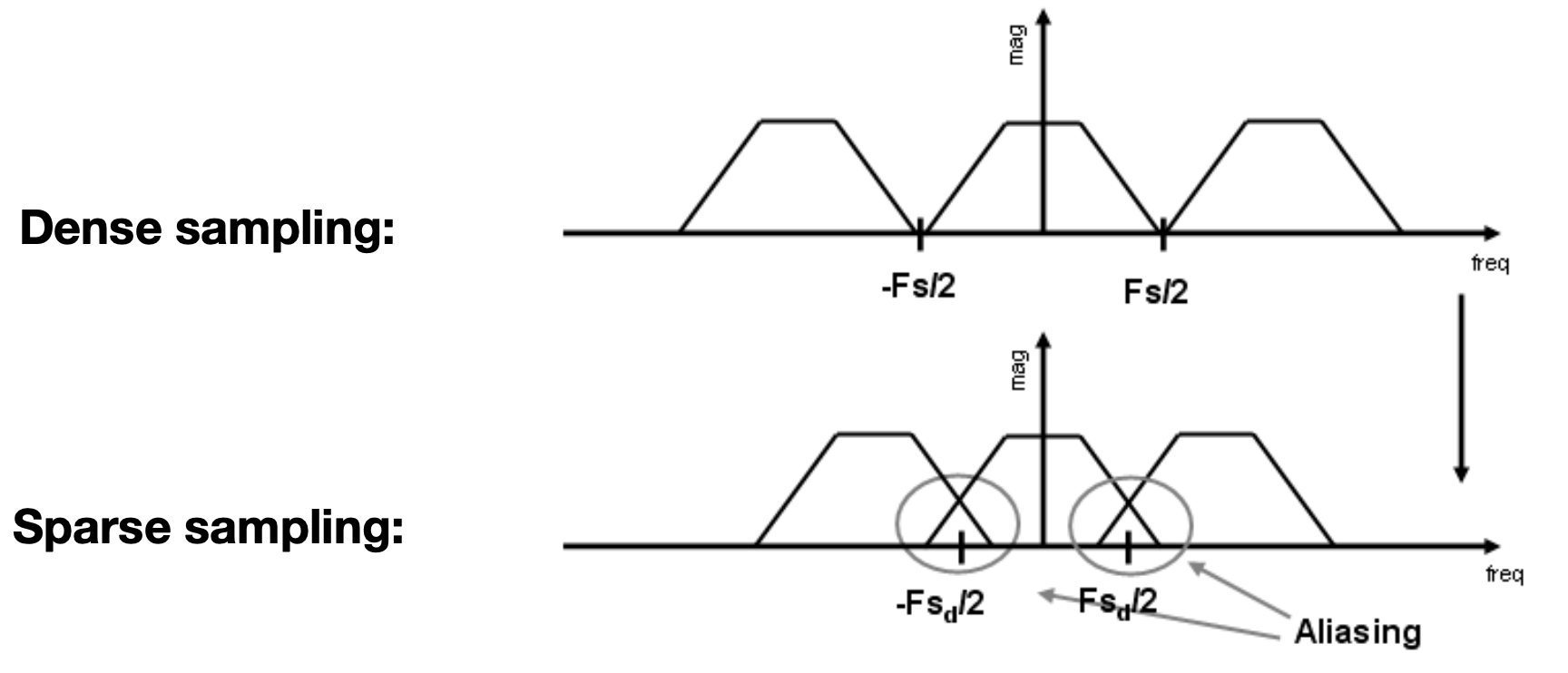
Antialiasing
介绍
How Can We Reduce Aliasing Error?
- Increase sampling rate：适用不同设备，成本太高；
- Essentially increasing the distance between replicas in the Fourier domain
- Higher resolution displays, sensors, framebuffers…
- But: costly & may need very high resolution
- Antialiasing：可以应用在同一设备上，主要策略；
- Making Fourier contents “narrower” before repeating
- i.e. Filtering out high frequencies before sampling
idea: limiting, then repeating
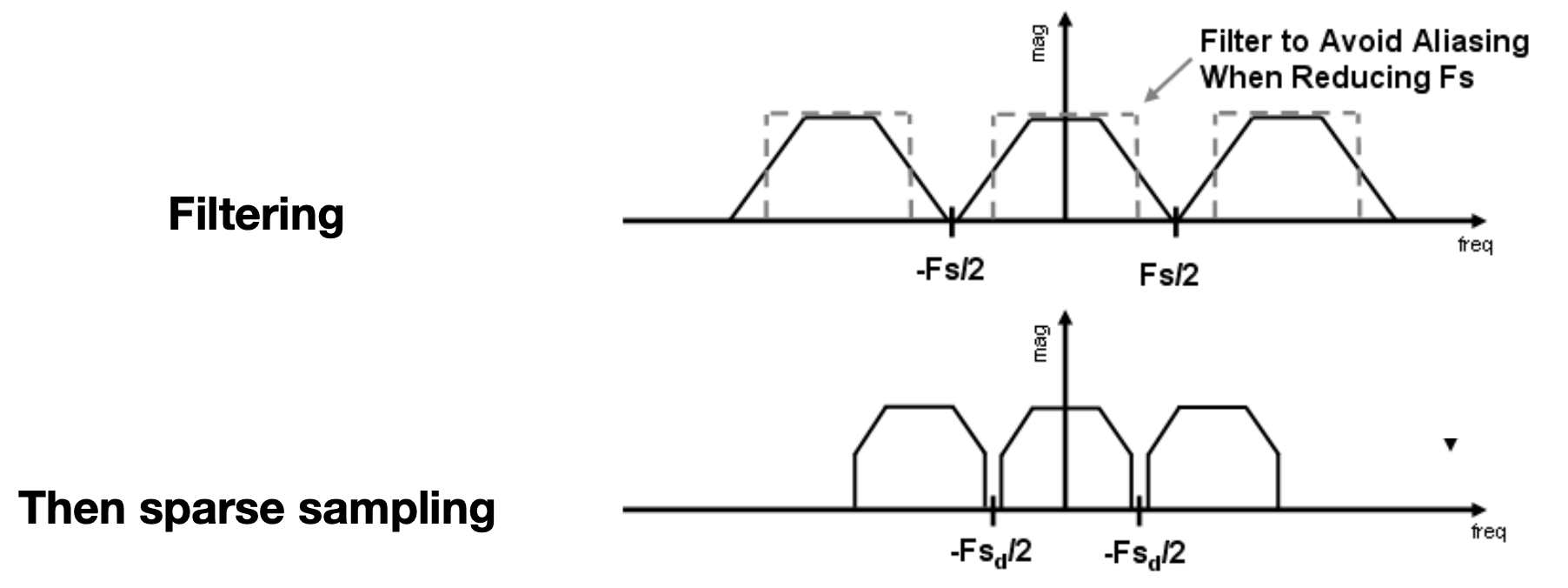
既然通过先模糊再采样的方法可以有效反走样，采样的方法已知，需要解决的是如何进行模糊的问题？
A Practical Pre-Filter
Antialiasing By Averaging Values in Pixel Area.
A 1 pixel-width box filter (low pass, blurring)
具体操作过程：
- Convolve $f(x,y)$ by a 1-pixel box-blur
- Then sample at every pixel’s center
In rasterizing one triangle, the average value inside a pixel area of $f(x,y) = \text{inside}(\text{triangle},x,y)$ is equal to the area of the pixel covered by the triangle.
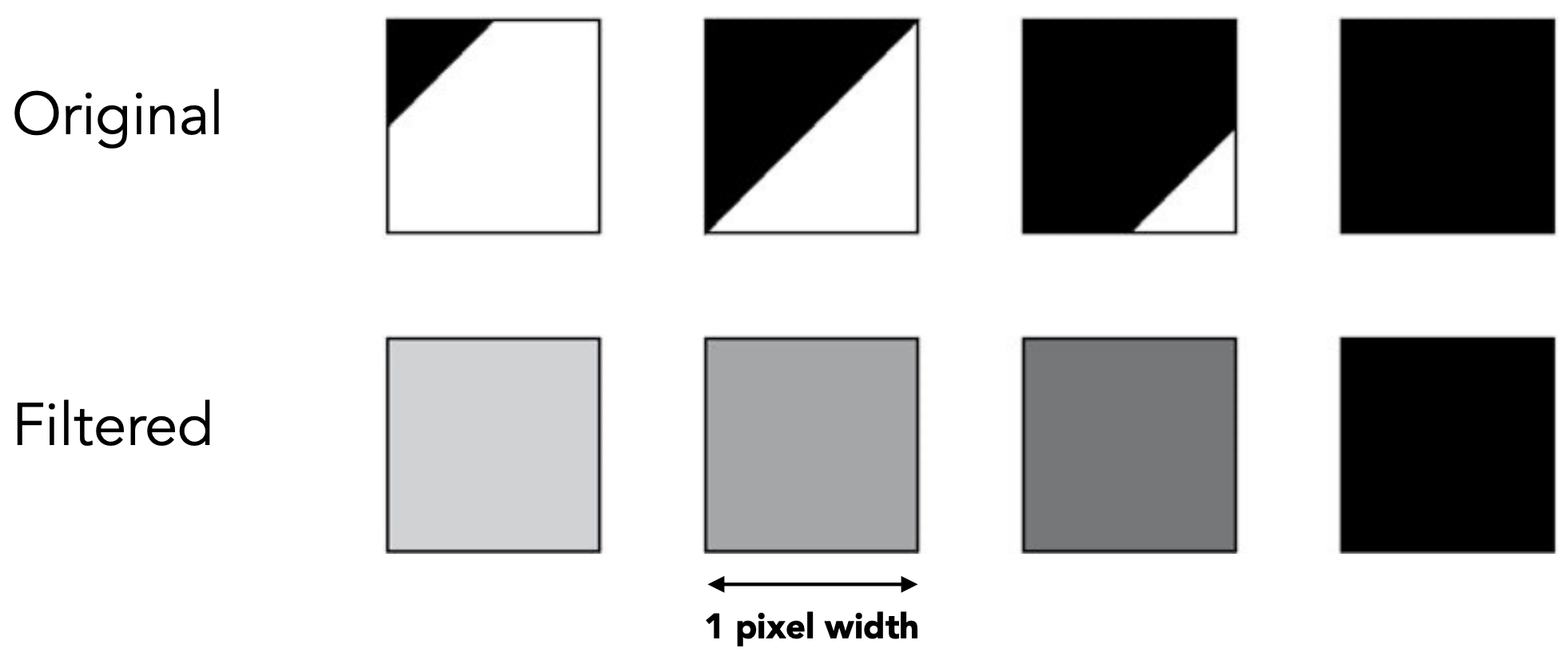
如何实现1 pixel-width box filter
对反走样解决方案的近似，不能严格解决反走样的问题。
Supersampling (MSAA)
Approximate the effect of the 1-pixel box filter by sampling multiple locations within a pixel and averaging their values.
将一个像素分成若干个小像素，然后再执行具体的操作。之前的方法，只需要针对一个像素本身判断是否在三角形内，现在需要针对一个像素中划分的更小的单元判断是否在三角形内，然后对整个像素进行平均。
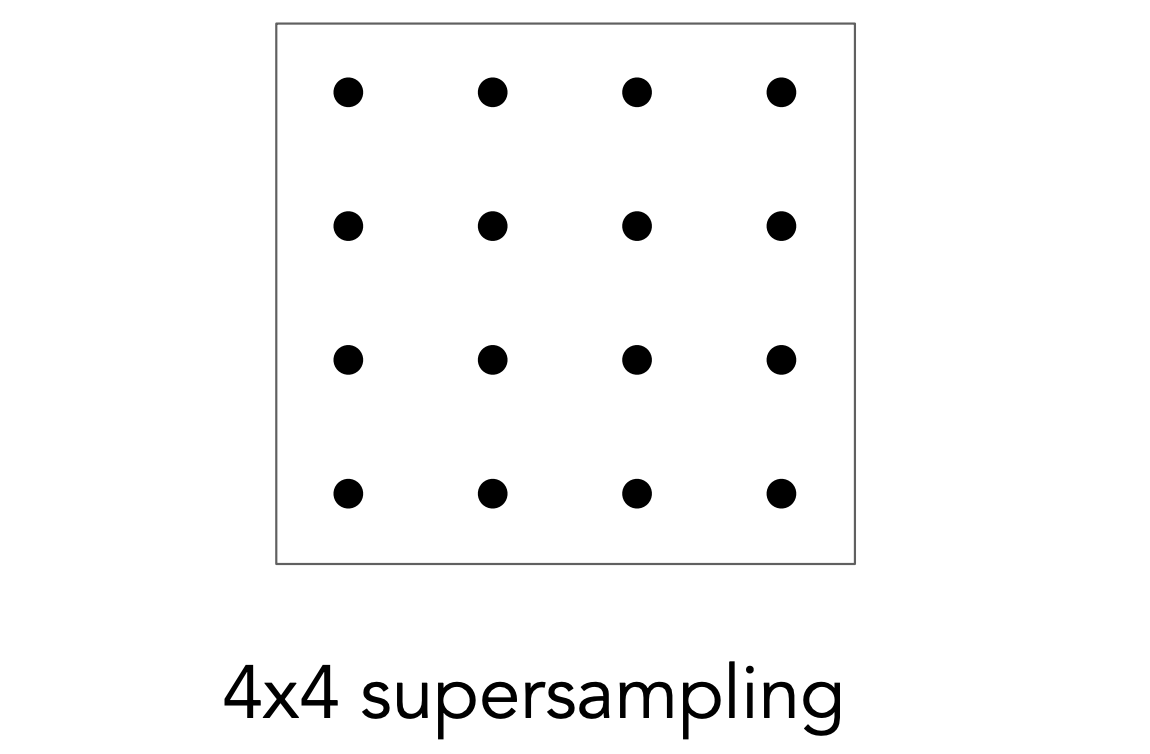
代价
MSAA增加了计算量，依赖将一个像素分割的方法。例如：如果是$4 \times 4$ ，则计算量增加了16倍，每个更小的像素中的点均要判断是否在三角形内。
优化方法
MSAA中将一个像素进行了均匀的划分，但是在实际中更多的是采用不太规则的划分，这样一个更小的单元可以被多个像素点进行共享，使得在判断该单元在三角形内的操作并不是严格是之前的16倍（在$4 \times 4$ 的划分下），因此效率会有提升。
工业界广泛使用的方法
- FXAA (Fast Approximate AA)：与采样无关的方法，在图像操作上的抗锯齿，基本思路是先模糊，然后将模糊后的图像中的锯齿去掉；
- TAA (Temporal AA)：复用上一帧的结果；
区别概念 Super resolution
- From low resolution to high resolution
- Essentially still “not enough samples” problem
- DLSS (Deep Learning Super Sampling): 使用深度学习来“猜测”图像放大后缺失的信息，这些缺失后的信息如果没有补全则会出现“锯齿”问题。
