GAMES101-06-2：Rasterization - Z-Buffering

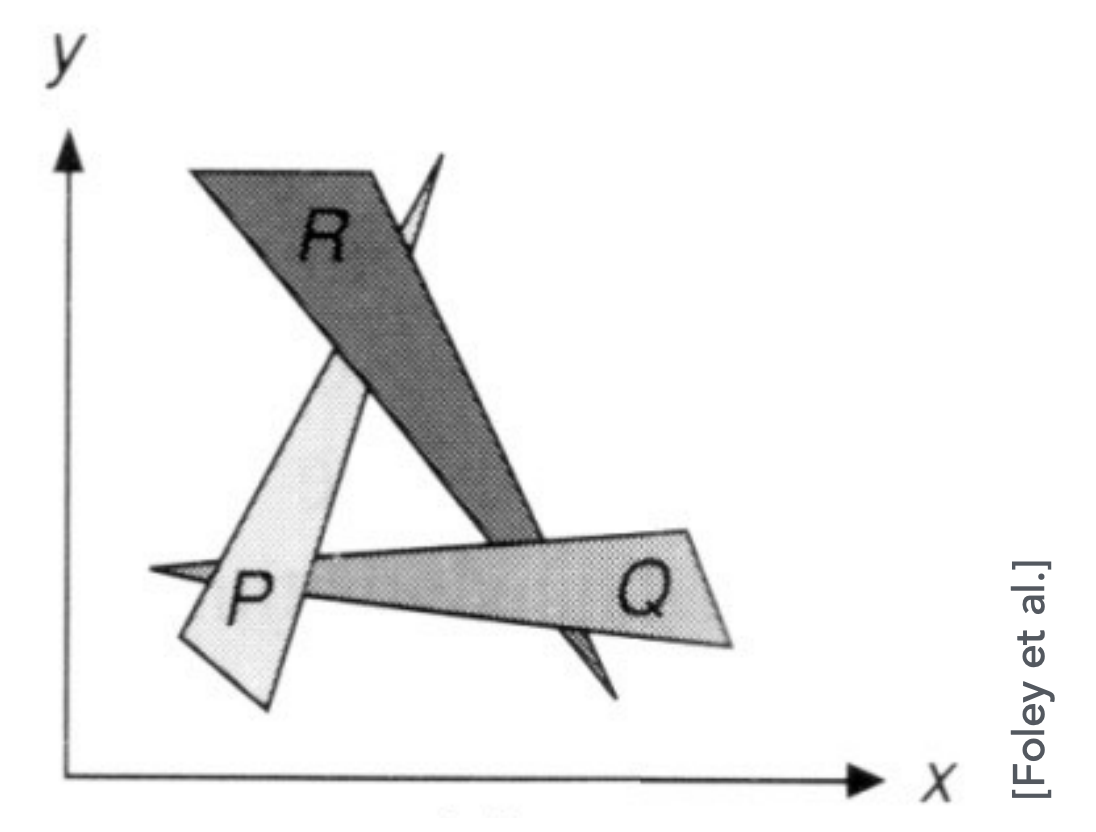
问题：Visibility / occlusion

很多不同的三角形彼此重叠，与相机之间也存在不同的距离，

Painter’s Algorithm

• Inspired by how painters paint
• Paint from back to front, overwrite in the framebuffer

朴素想法

• Requires sorting in depth $(O(n \log n)$ for n triangles)

存在问题

• Can have unresolvable depth order：有时无法得到深度排序；
• 因此实际中不会使用该算法；

Z-Buffer

想法

• Store current min. z-value for each sample (pixel) 所有操作都是针对像素来说的；
• Needs an additional buffer for depth values
  • frame buffer stores color values：对应最后的结果；
  • depth buffer (z-buffer) stores depth：对应深度缓存的图；

备注：For simplicity we suppose $z$ is always positive (smaller $z$ -> closer, larger $z$ -> further)。

例子

深度值小，对应的是黑色。

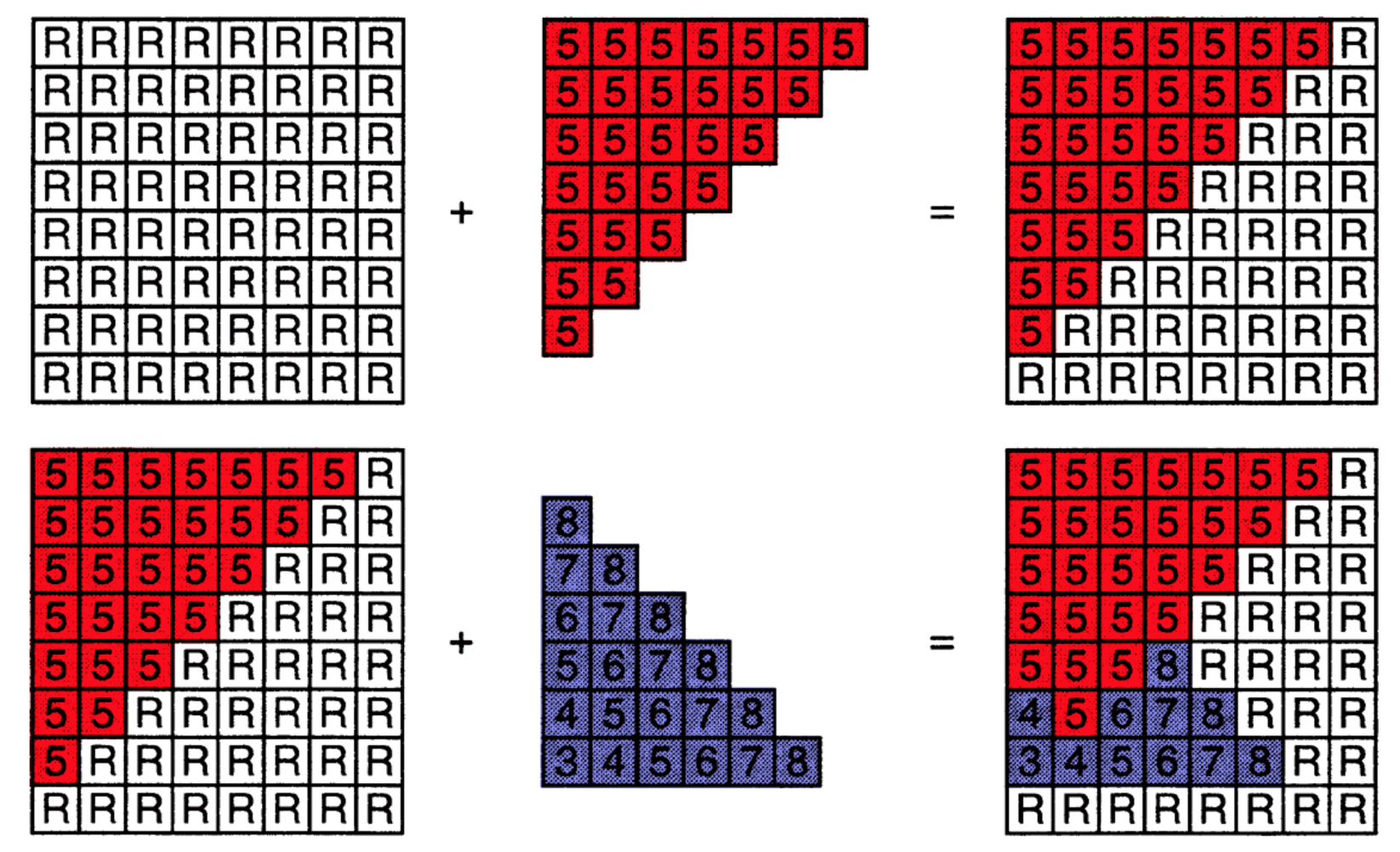
Z-Buffer Algorithm

Initialize depth buffer to +inf
During rasterization:
for (each triangle T)
    for (each sample (x,y,z) in T)
        if (z < zbuffer[x,y]) // closest sample so far
            framebuffer[x,y] = rgb; // update color
            zbuffer[x,y] = z; // update depth
        else
            ; // do nothing, this sample is occluded

Z-Buffer Complexity

Complexity

• $O(n)$ for n triangles (assuming constant coverage)

How is it possible to sort n triangles in linear time?

• 这里并没有对深度信息进行排序；

Drawing triangles in different orders?

• 结果仍然相同，绘制三角形的顺序不影响最终的结果（不同三角形之间的深度值不存在重复）。

总结

• Most important visibility algorithm
• Implemented in hardware for all GPUs