问题
前面的Blinn-Phong Model是针对单个shading point进行着色,下一步是针对具体的物体进行着色。
对于同样的几何物体,不同的着色频率会导致不同的结果,如下图:

- 图1是针对一个面进行着色,即在一个面上只着色一次;
- 图2是针对三角形的顶点进行着色,然后三角形内部通过插值补全其他的着色区域;
- 图3是针对每个像素进行着色,通过计算三角形顶点的法线方向,然后对每个像素的法线方向进行插值,然后进行着色;
这三种方法,效果是越来越好,但是计算量也是越来越大。
Flat shading: shade each triangle
- Triangle face is flat — one normal vector
- Not good for smooth surfaces

Gouraud shading: shade each vertex
- Interpolate colors from vertices across triangle
- 插值的内容在后续的课程中提供;
- Each vertex has a normal vector

Defining Per-Vertex Normal Vectors
From the underlying geometry
Best to get vertex normals from the underlying geometry:过于理想;
- e.g. consider a sphere
利用邻居进行平均
一般化的方法: infer vertex normals from triangle faces
- 简单方法: average surrounding face normals; 其中 N_v是顶点的法线向量,$N_i$ 是该顶点相邻的三角形的法线向量。计算完成后,需要将得到的法线向量归一化,因为只关心方向。
$$
N_v = \frac{\sum_{i}{}N_i}{\Vert \sum_{i}{}N_i \Vert}
$$
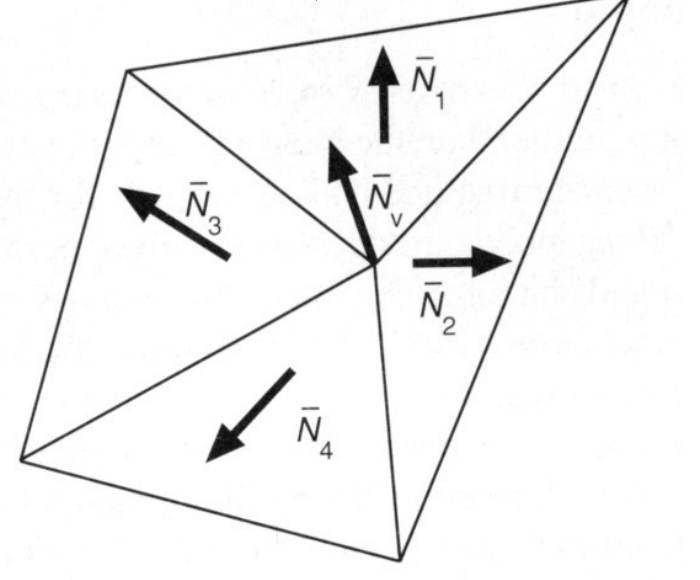
- 加权平均:按照三角形面积进行法线向量的平均;
Phong shading: shade each pixel
- Interpolate normal vectors across each triangle
- Compute full shading model at each pixel
- Not the Blinn-Phong Reflectance Model:与Phong shading均为同一个人提出的;

Defining Per-Pixel Normal Vectors
根据之前得到了三角形顶点的法线向量,可以利用顶点的法线向量进一步得到每个像素的向量,这里需要利用 Barycentric interpolation of vertex normals 来完成,后续会介绍。
对比
这三种方法不一定是哪种一定最好,如下图:当物体的顶点很多时,或者三角形很密集时,使用简单的Face shading效果也不错。


