Texture Mapping
问题
一个物体的不同区域使用了相同的着色模型,但是不同区域的漫反射系数 $k_d$ 不同,该系数的不同会导致出现不同的纹理 texture。
之前提到的着色模型未过多考虑shading point本身的性质,只提到了漫反射系数、镜面反射系数等,但是着色区域本身存在很多不同的性质,这些性质均会影响shading的效果。因此,本质上纹理是逐shading point改变其自身的性质,使得即便在相同的着色模型下,其着色的效果也会有差异。
那么如何定义着色区域的不同性质呢?引入纹理映射。
定义shading point的基本属性
Idea: Surfaces are 2D
- Surface lives in 3D world space
- Every 3D surface point also has a place where it goes in the 2D image (texture).
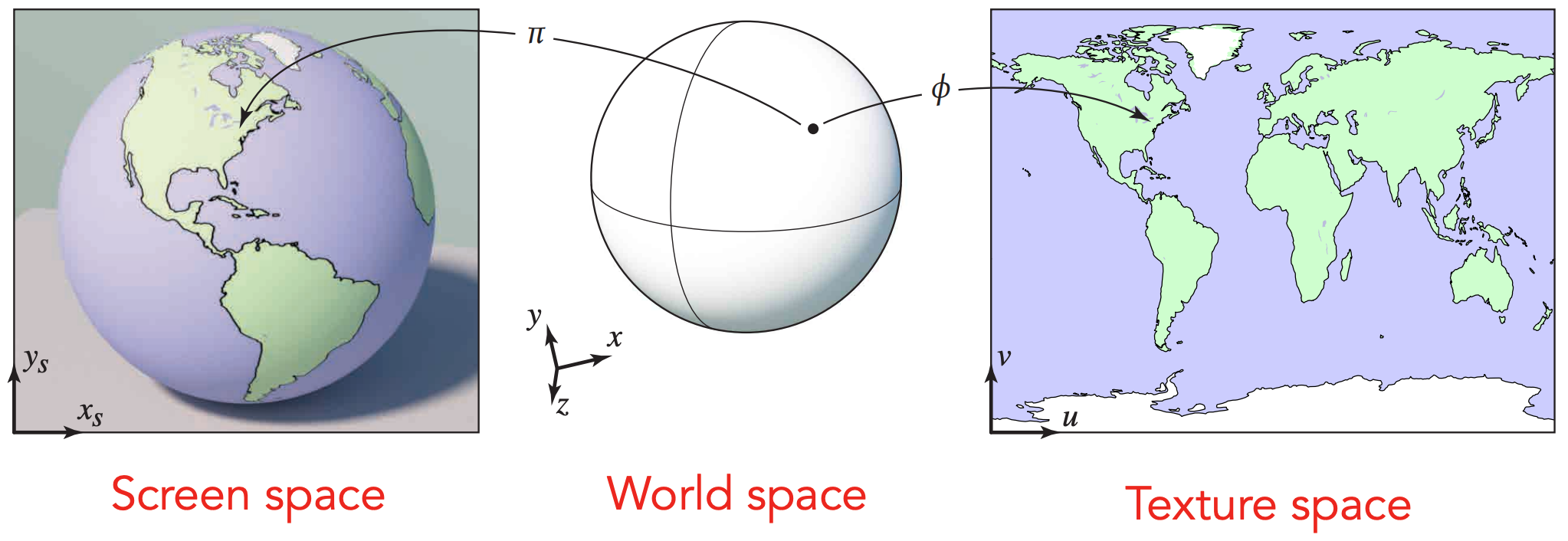
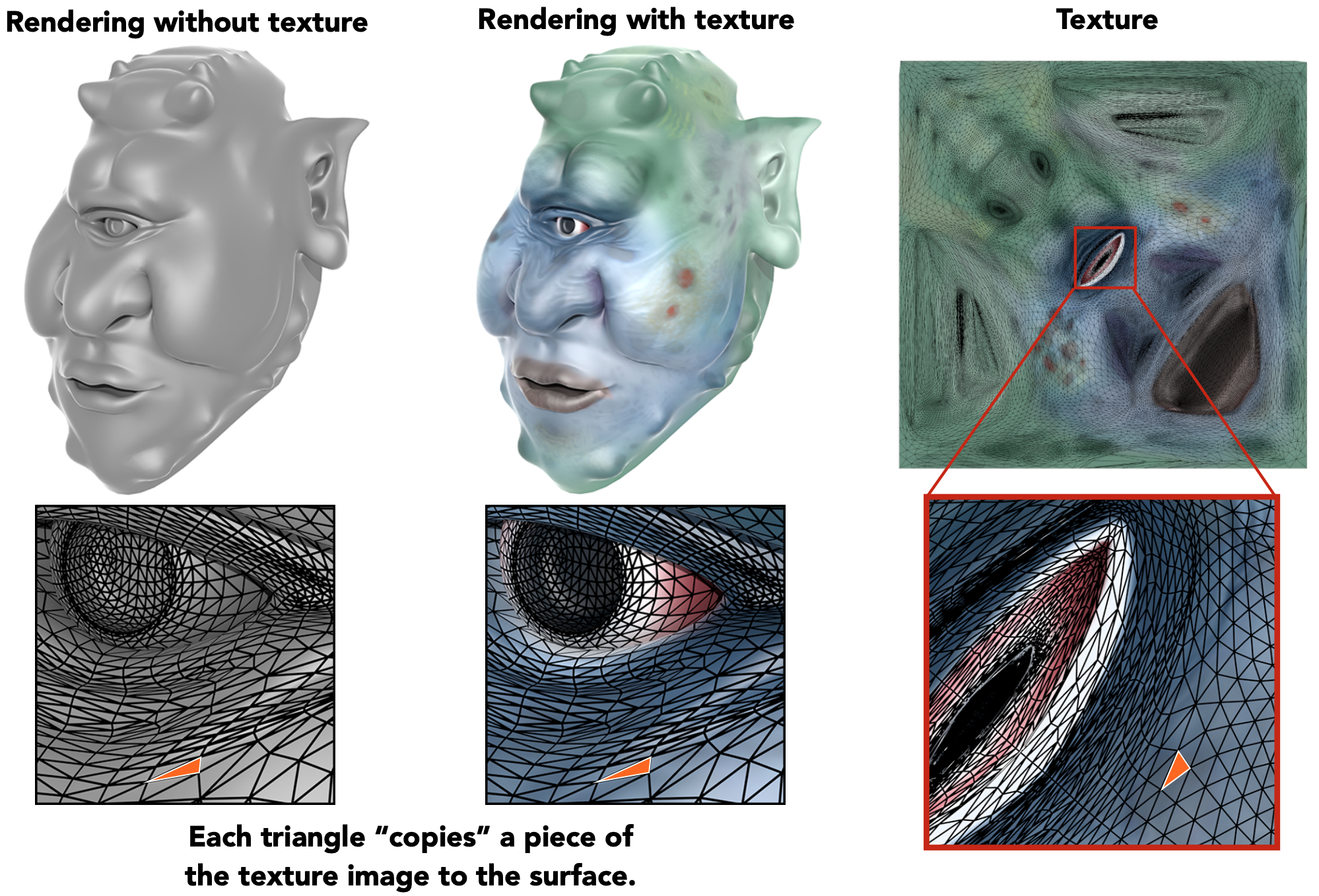
纹理如何应用:Texture Applied to Surface
需要建立三维物体中的三角形与纹理中的三角形的映射关系,保证两者一一对应,同时尽可能少地出现拉伸等情况。
这种对应关系可以由艺术家完成创造,或者自动化实现。本课中,默认两者已经建立了映射关系,即物体上的每一点均在纹理上有对应的坐标,只需利用这个关系即可。
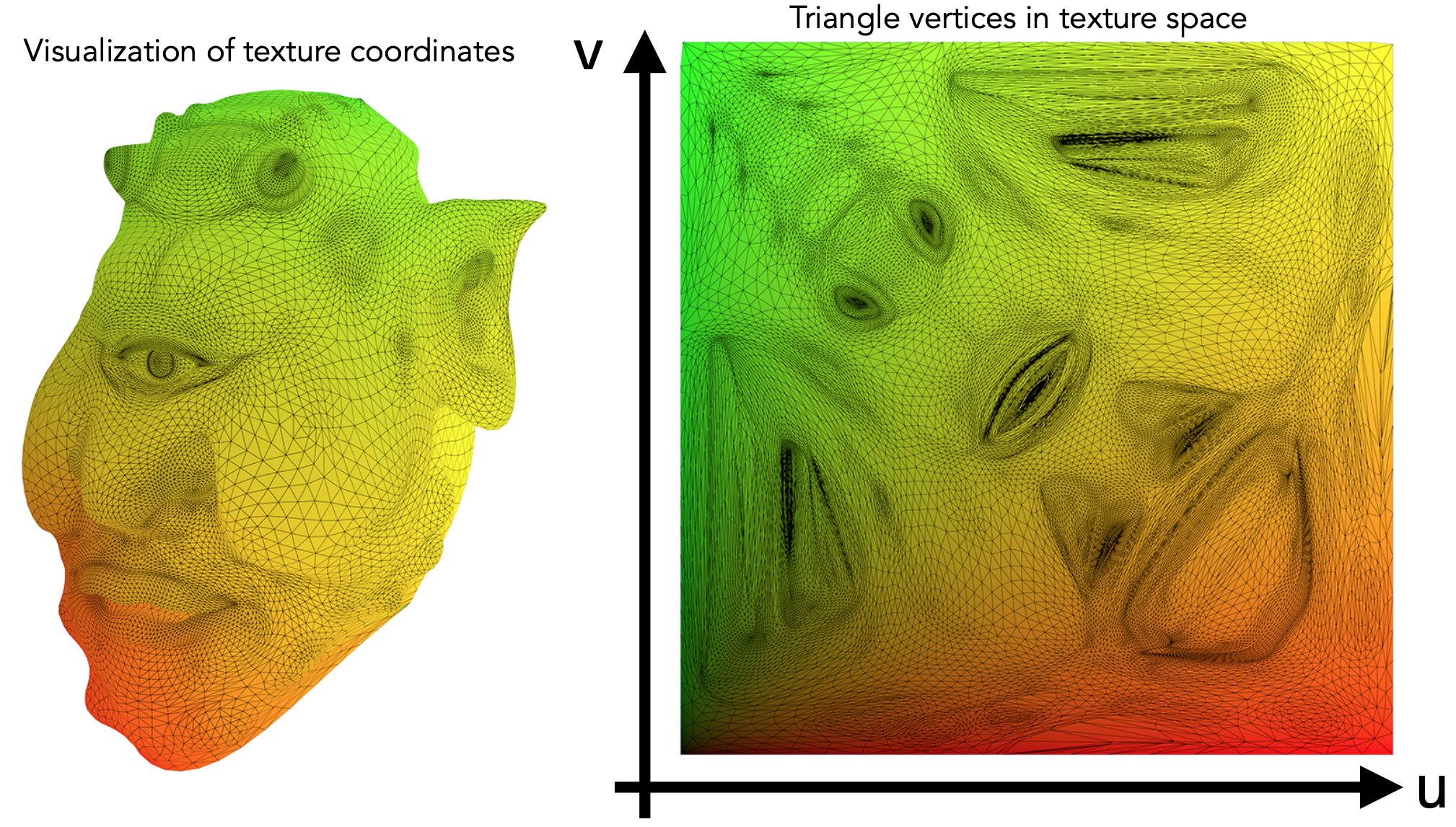
纹理坐标
Each triangle vertex is assigned a texture coordinate $(u,v)$,两个方向的坐标均在$(0,1)$内,以便处理,不考虑其真实像素是多少。
Textures can be used multiple times
在纹理映射中,物体上的多个区域可能对应相同的纹理区域,即纹理可以使用多次,当多次使用时,会在相同纹理之间出现不必要的界限,因此如何在多次使用中使相同的纹理之间的过度比较平滑是一个问题。
Interpolation Across Triangles
问题
到目前为止,有两个应用场景需要进行插值:
- Specify values at vertices shading frequencies 中的 Gouraud shading和Phong shading分别需要对顶点和像素计算法线向量,然后在三角形内部计算相应的颜色等属性;
- Obtain smoothly varying values across triangles 在三维物体与纹理映射中,三角形的顶点在纹理中有相应的纹理坐标,但是三角形内的区域需要通过插值计算相应的纹理坐标,以实现纹理覆盖到物体表面时,能够自然平滑的过度。
插值针对的对象
Texture coordinates, colors, normal vectors, …
实际上可以对任意属性进行插值。
如何插值:Barycentric coordinates
定义
- 首先明确的是,重心坐标是定义在三角形上的,意思是每个三角形都有一个重心坐标系,当三角形不同时,其重心坐标也不同;
- 三角形内的任意一点 $(x, y)$ 均可以表示成三角形顶点的线性组合; $$
(x, y) = \alpha A + \beta B + \gamma C
$$ - 其中,称 $(\alpha, \beta, \gamma)$ 为 $(x,y)$ 的重心坐标,其中三者需要满足两个条件:
- 三者相加为1:保证点 $(x,y)$ 在三角形所在的平面上; $$
\alpha + \beta + \gamma = 1
$$ - 三者均为非负值:保证点 $(x,y)$ 在三角形内部; $$
\alpha \ge 0 \wedge \beta \ge 0 \wedge \gamma \ge 0
$$
- 三者相加为1:保证点 $(x,y)$ 在三角形所在的平面上; $$
Geometric viewpoint — proportional areas
计算三角形内任意一点的重心坐标,可以从几何面积的角度考虑。
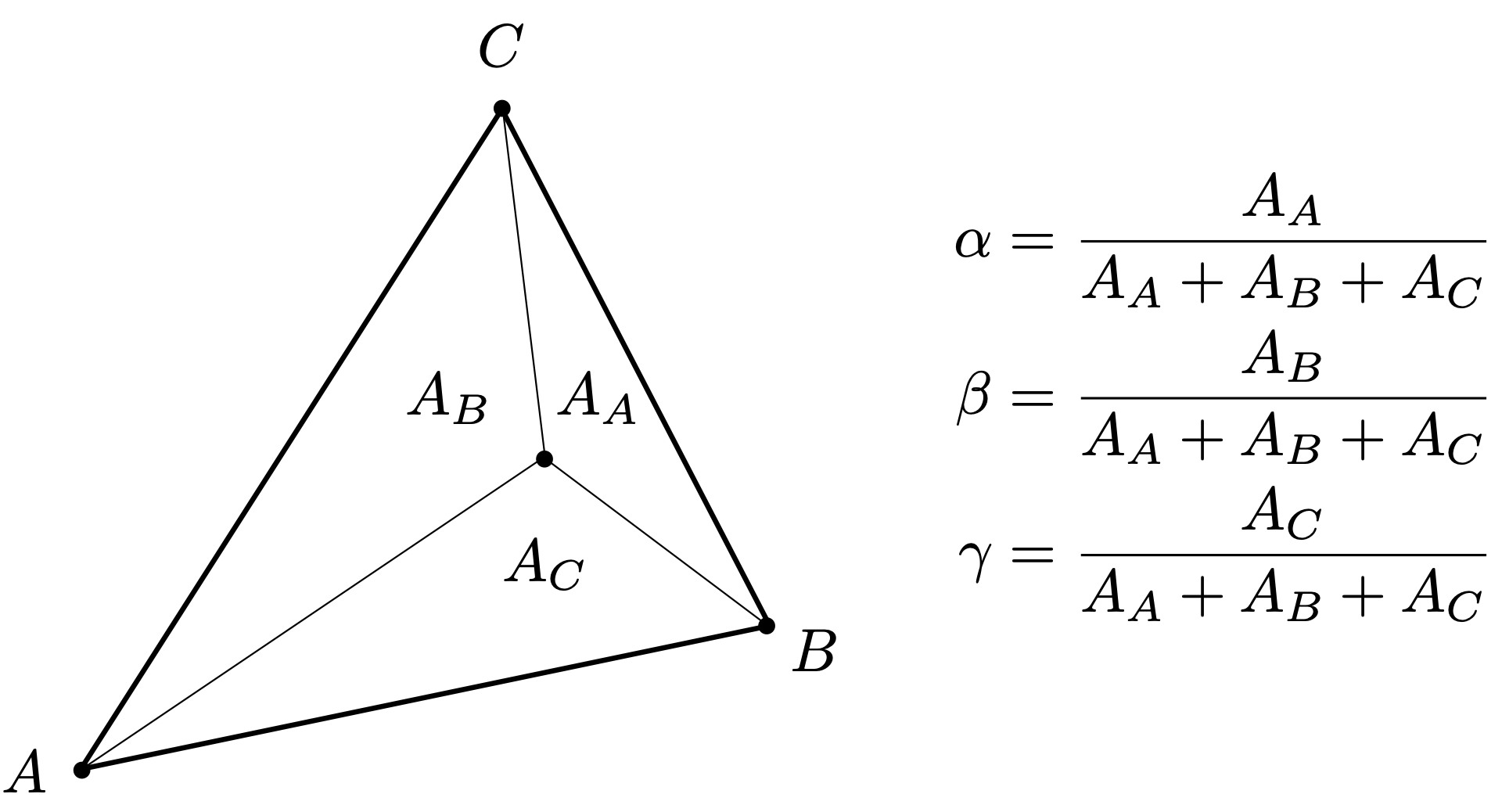
三角形的重心的重心坐标:
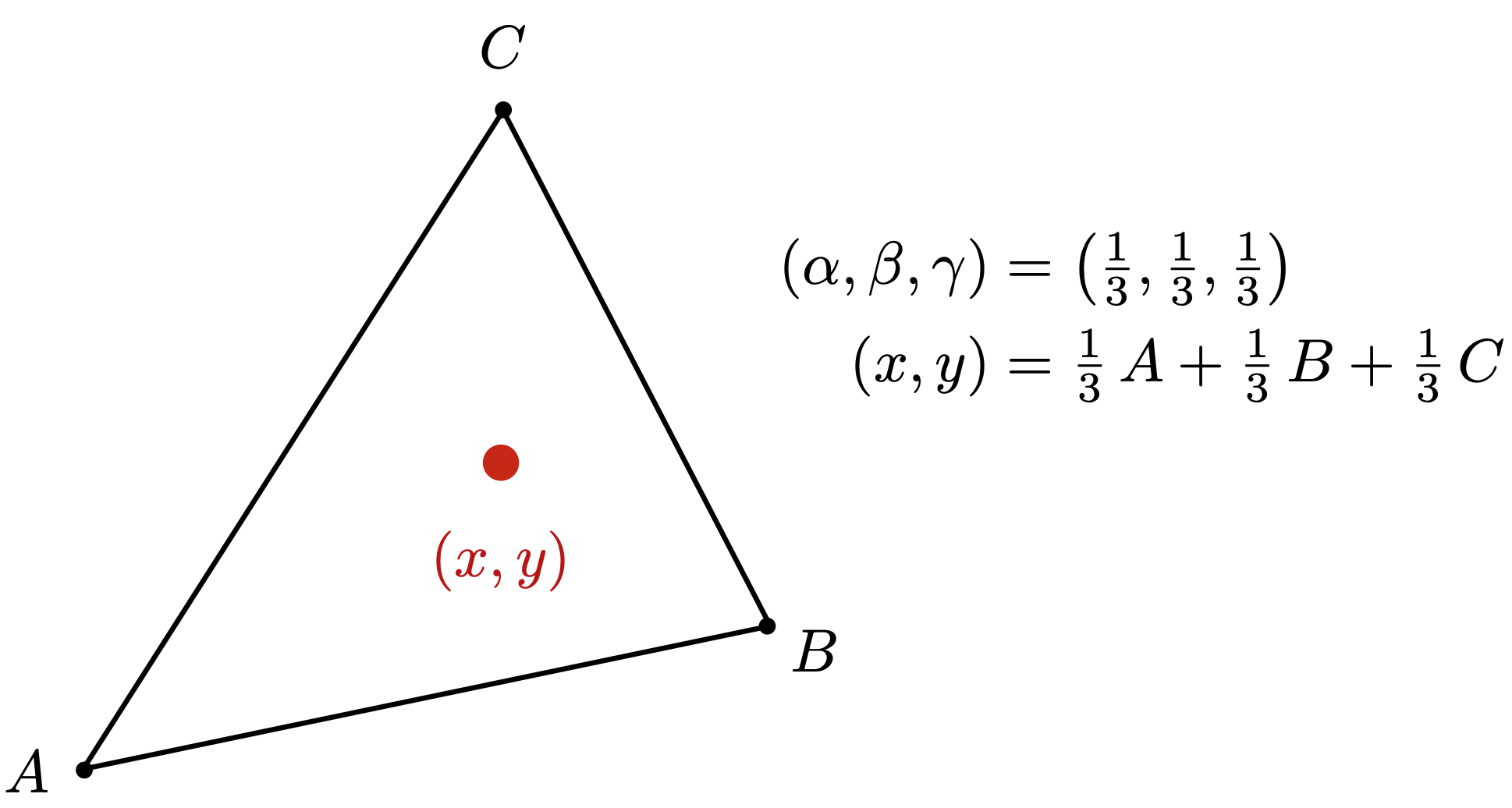
一般化计算公式
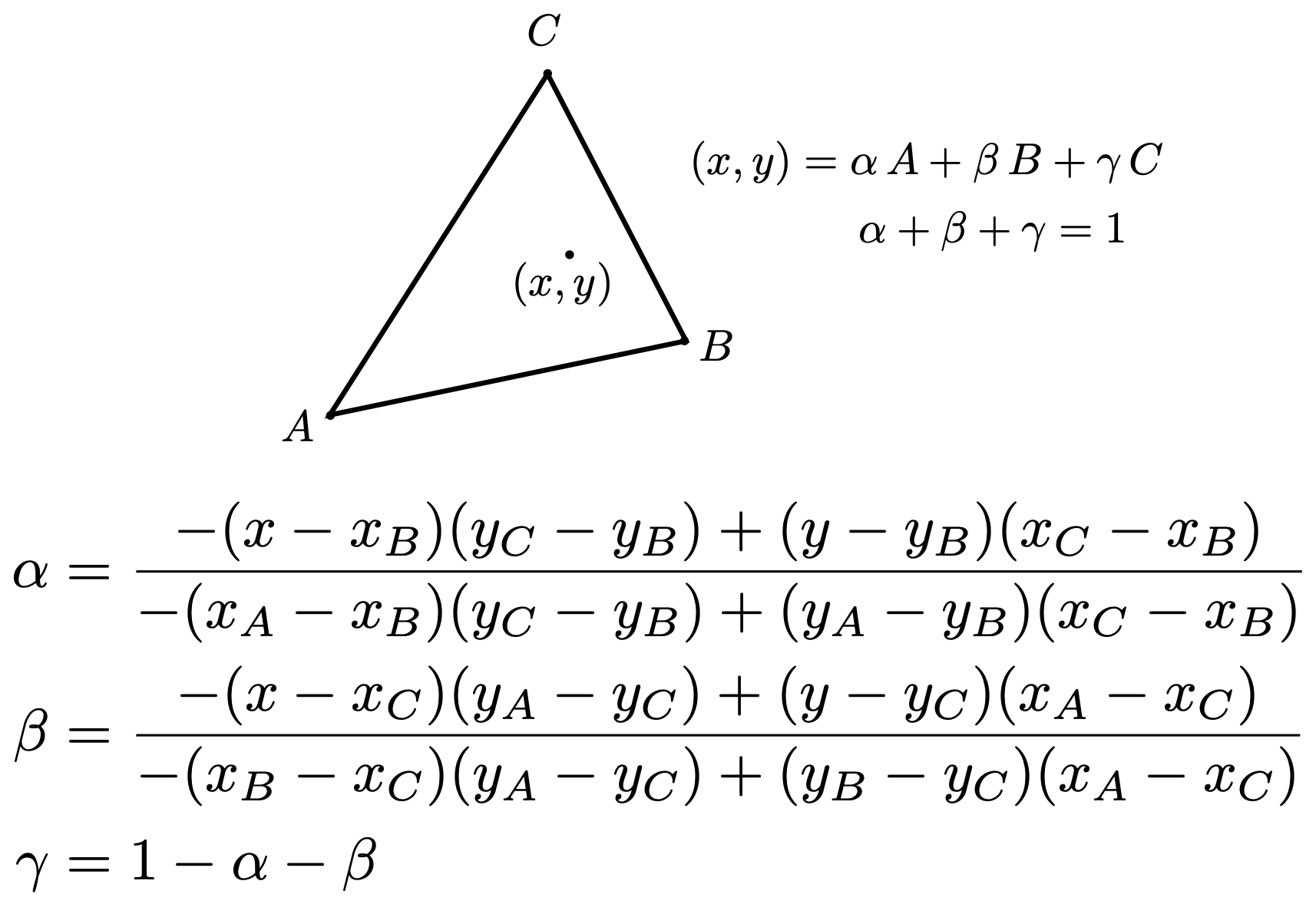
Using Barycentric Coordinates
当针对三角形内任意一点计算得到对应的重心坐标后,可以利用该重心坐标对任意的属性进行插值,所谓的插值,在这里指的就是通过对三角形顶点属性的线性组合得到自身的属性。
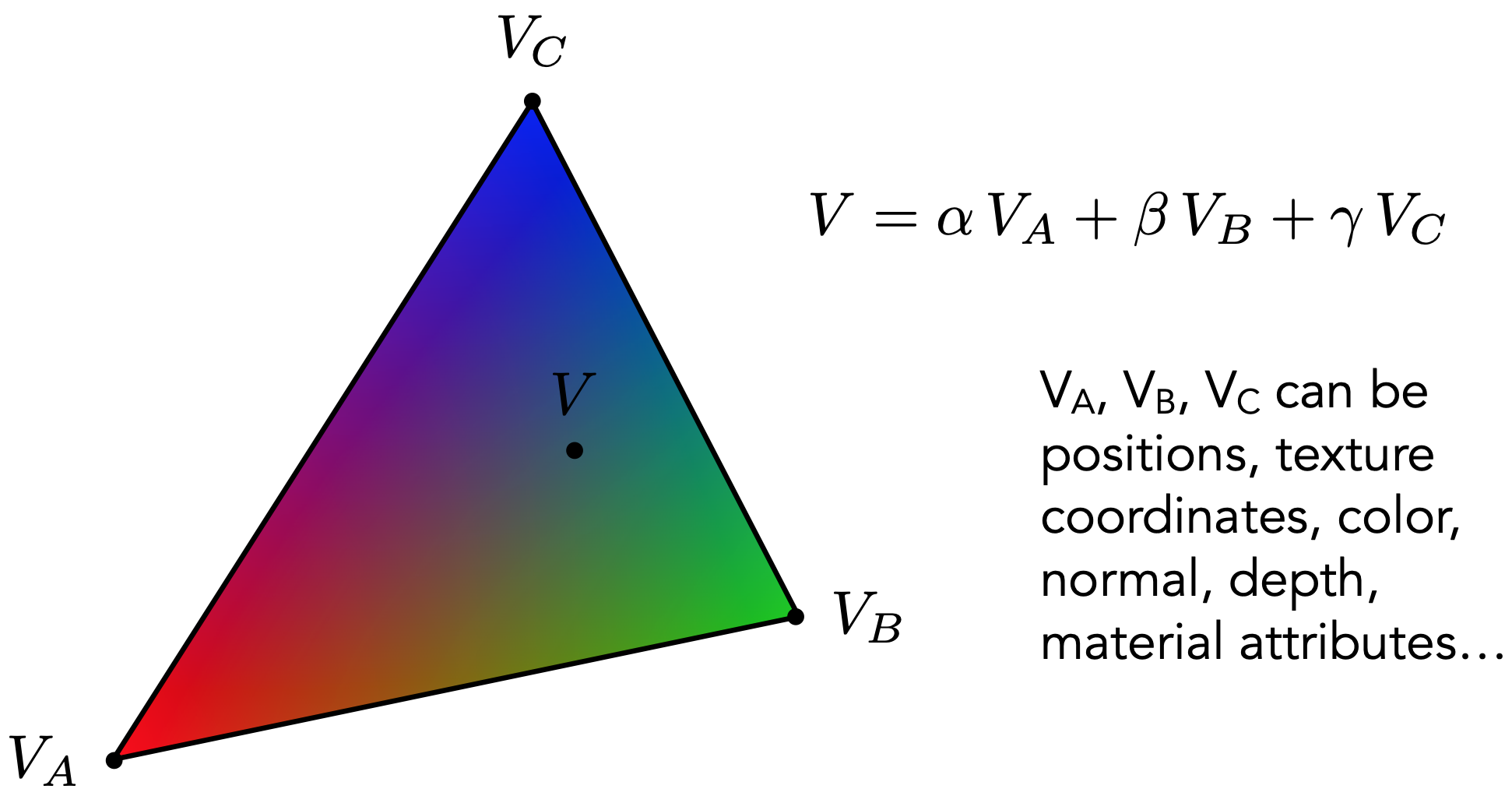
注意事项
However, barycentric coordinates are not invariant under projection!
在三角形完成投影后,三角形内任意一点的重心坐标可能发生变化。因此针对3D中的三角形进行插值时,需要利用3D坐标进行插值,而不是利用投影后的2D坐标进行插值,例如:在对3D物体的深度信息时进行插值时。

