GAMES101-09-2：Shading - Texture Mapping - Applying Textures

应用例子：Diffuse Color

for each_rasterized_screen_sample(x,y):          // Usually a pixel’s center
    (u,v) = evaluate_texture_coordinate_at(x,y)  // Using barycentric coordinates
    texcolor = texture.sample(u,v);
    set_sample_color_to_texcolor();              // Usually the diffuse albedo Kd

简单来说，这个过程可以总结为：

1. 对于每个经过光栅化的像素，首先计算其重心坐标；
2. 根据光栅化后的三角形中顶点与纹理坐标的映射关系（视为已知），利用三角形中任意一点的重心坐标，插值得到其对应的纹理坐标；
3. 利用得到的纹理坐标得到纹理信息 texcolor；
4. 将该纹理信息设置到光栅后的三角形内部，即实现将纹理“贴到”物体上，上例中是将纹理信息视为漫反射系数。

这个过程比较简单，但是会产生问题。

问题：Texture Magnification 纹理太小

问题描述

纹理的分辨率很小，但是待渲染的物体分辨率很高，这会产生什么问题？在物体上的多个像素点可以对应纹理上的同一个texel（A pixel on a texture — a texel），例如通过对得到的纹理坐标四舍五入，取最临近的纹理坐标，因此可能会出现问题。

Nearest

最直接的方法：直接四舍五入取最近的纹理坐标。

Bilinear

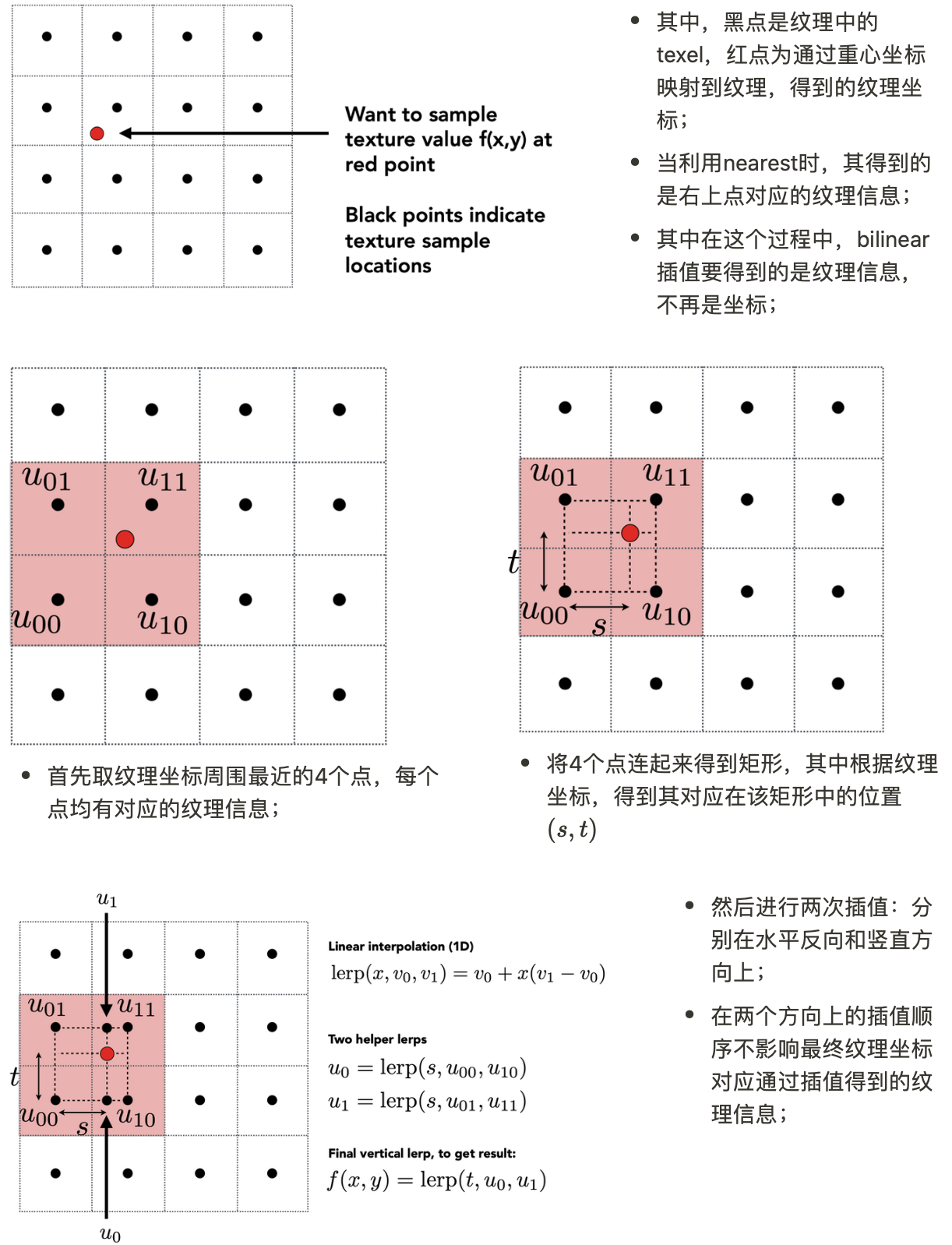
考虑最终的效果和计算复杂度，bilinear得到了很好的平衡。

Bicubic

使用周围的16个texel进行插值，效果更好，但是计算量更大。

问题：Texture Magnification 纹理太大

问题描述

在应用texture时，采用上例Diffuse Color中使用的方法，很简单，但是由于只是对纹理中的一个点进行采样。当纹理过大时会出现问题，如下图中在近处出现锯齿，在远处出现摩尔纹。

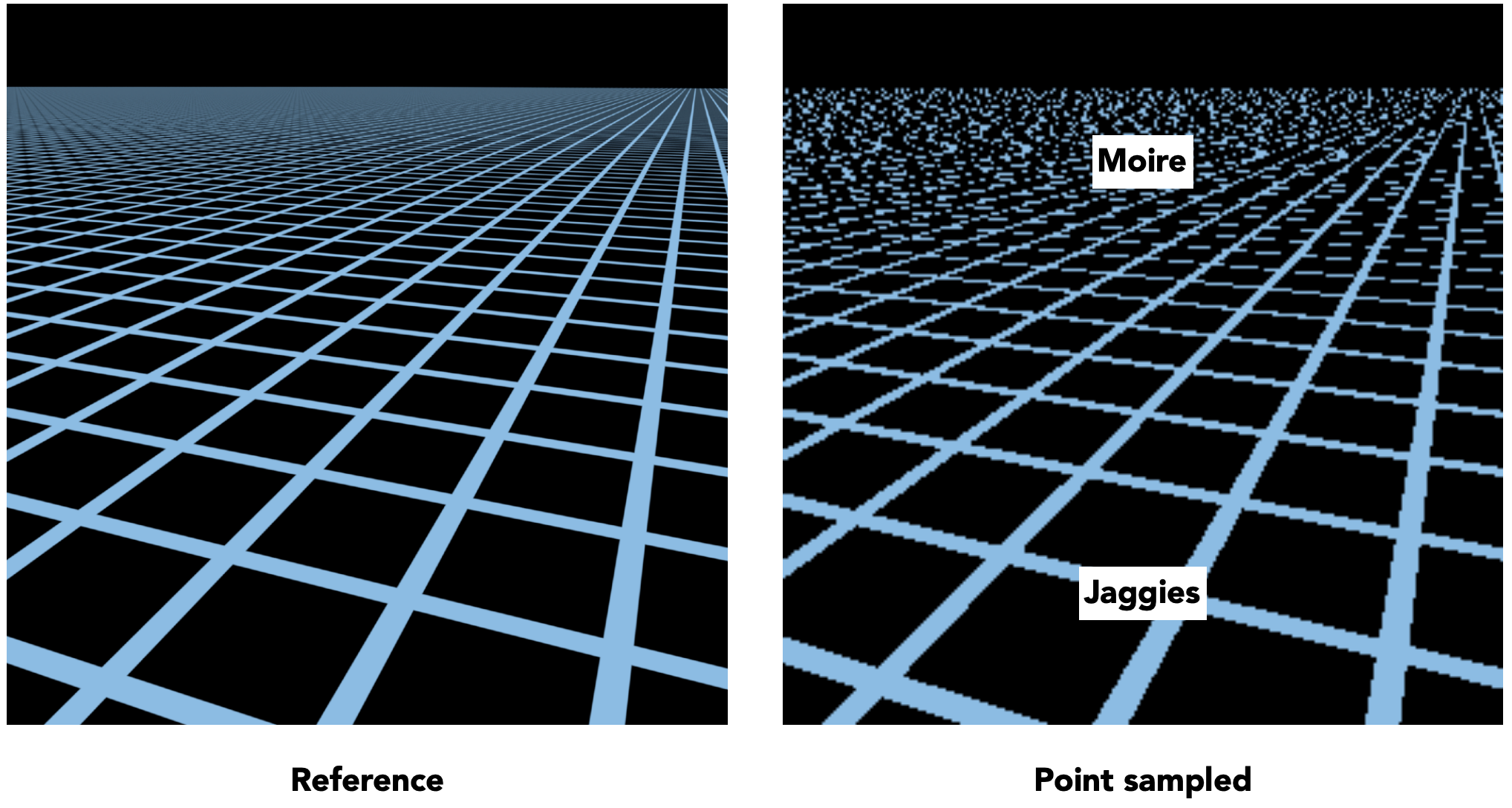
原因剖析

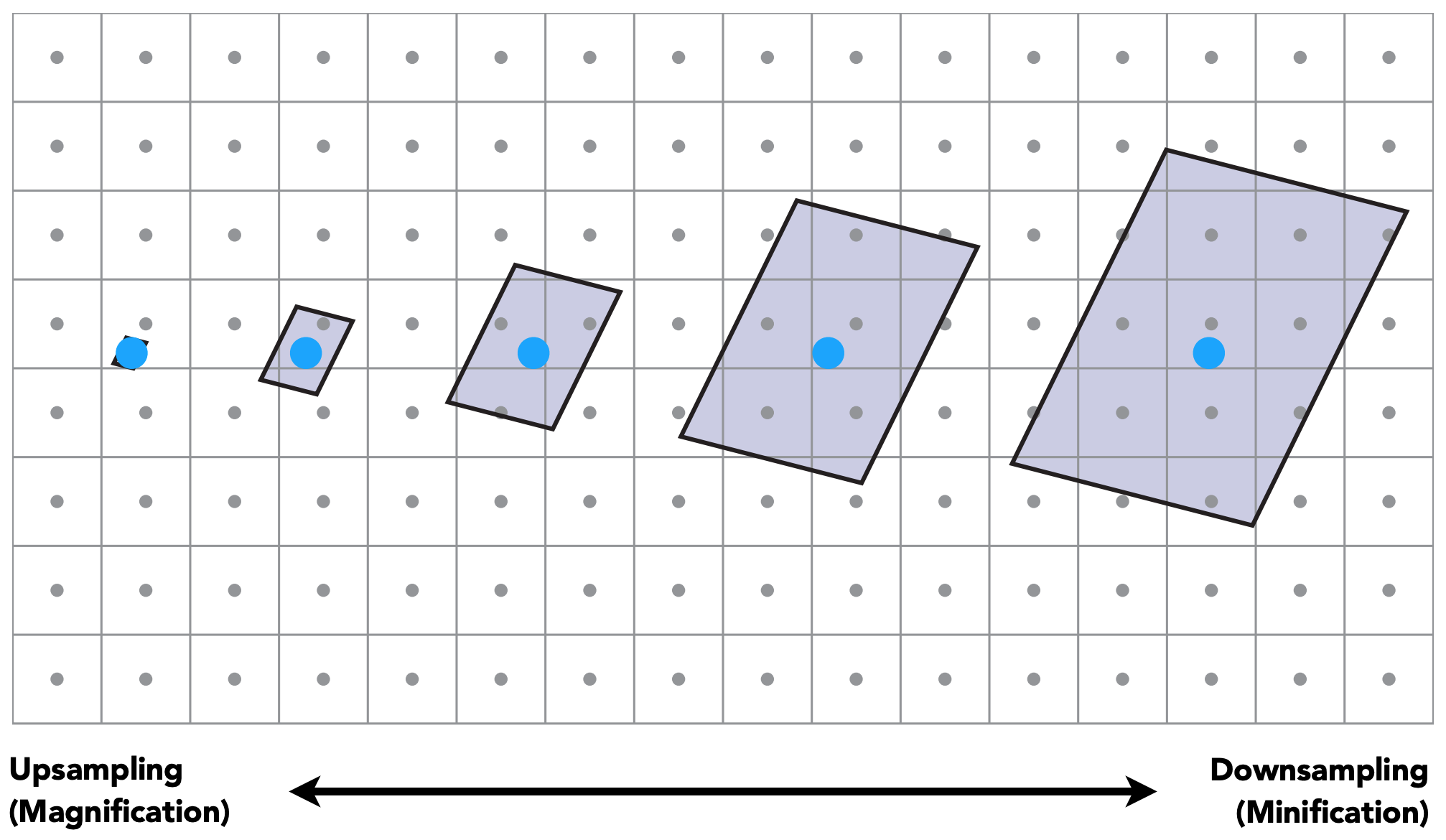
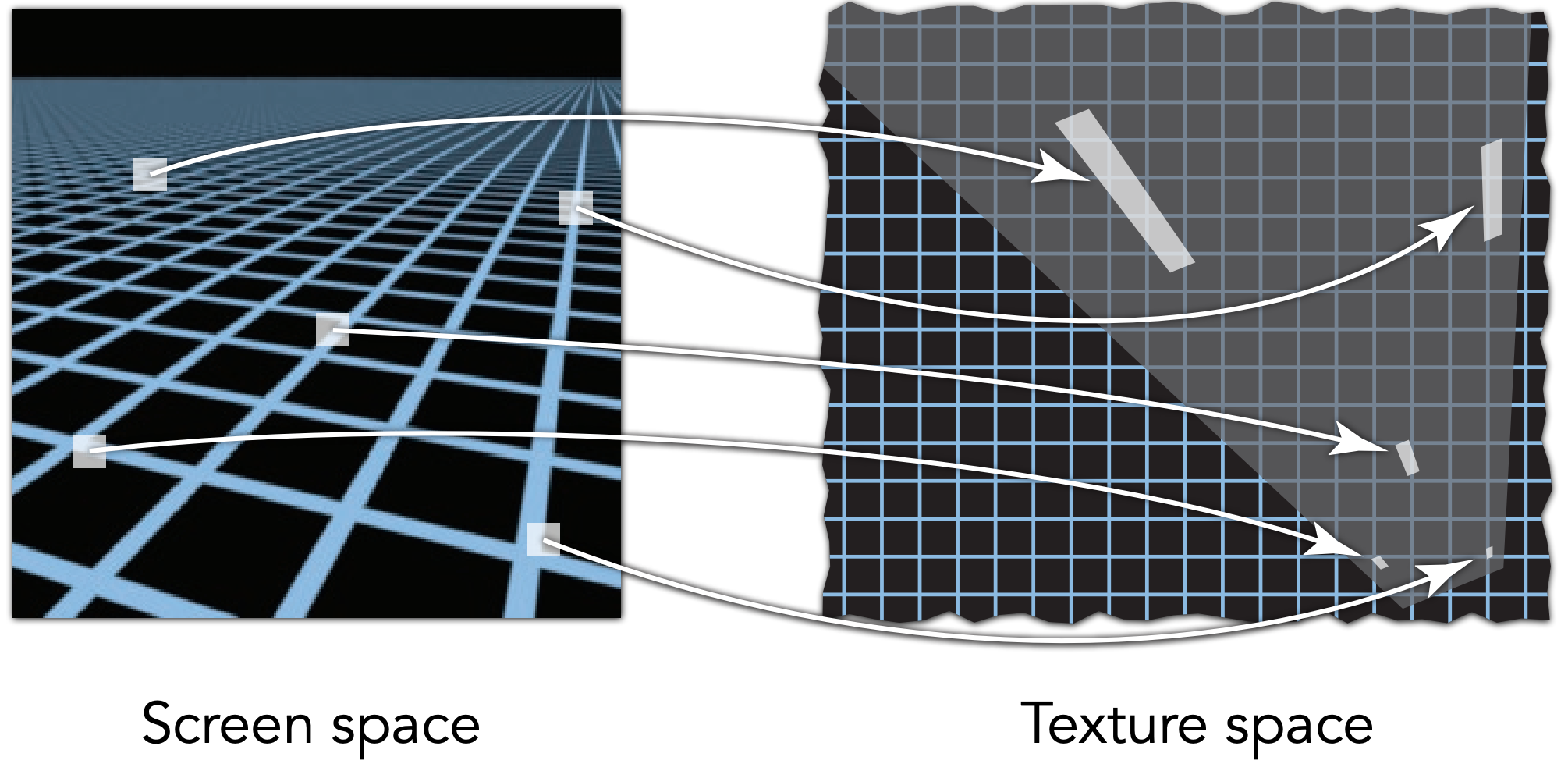
如上图所示，从左到右对应上图中从近到远：

• 在近处：一个像素对应纹理中的texel较少；
• 在远处时，一个像素对应纹理中的很多texel；

基于这种情况：

• 在近处，使用point sampling时，可以在纹理中直接采样对应的纹理信息，由于覆盖的纹理区域较小，因此直接采用对应的纹理信息，问题不大；
• 在远处时，由于覆盖的纹理区域较大，因此直接采用对应的一个点的纹理信息，会产生以偏概全的问题；

解决方案1：Supersampling Do Antialiasing

使用MSAA进行反走样可以解决问题。

为什么有效？

对于远处区域来说，由于覆盖的纹理区域较大，可以视为用像素中的低频信号采样纹理中的高频信号，因为很小的一块像素区域对应很大的纹理区域。

基于这种情况，MSAA的策略是将像素点划分为更小的单元，从而提高了采样频率，以实现反走样，能够解决该问题。

缺点

虽然这种方法能够解决问题，但是存在代价太大的问题，尤其是当远处的像素和近处的像素覆盖纹理区域的范围很悬殊时，对于像素的进一步划分，在近处的效果很好，但是在远处可能提升有限。同时，当远处的像素区域很小时，若要提升效果，可能需要划分更多的单元，但是在近处则带来计算代价的上升。

解决方案2：Range Query - Mipmap

idea

代替进行采样，直接获得像素覆盖的纹理区域的平均值，这相当于把之前的针对一个像素点的纹理信息的查询转换为特定区域内的范围查询，以便实现平滑的效果。

get the average value within a range.

Mipmap

Allowing (fast, approx., square) range queries.

该方法只能进行近似的、正方形区域的快速范围查询。

对于一个纹理图片来说，所谓mipmap指的是不断缩小图片的分辨率从而得到对应区域的纹理信息，上图中虽然所有的图片都是相同尺寸，这是为了展示效果，实际中每次缩小，尺寸均变为原来的0.25。

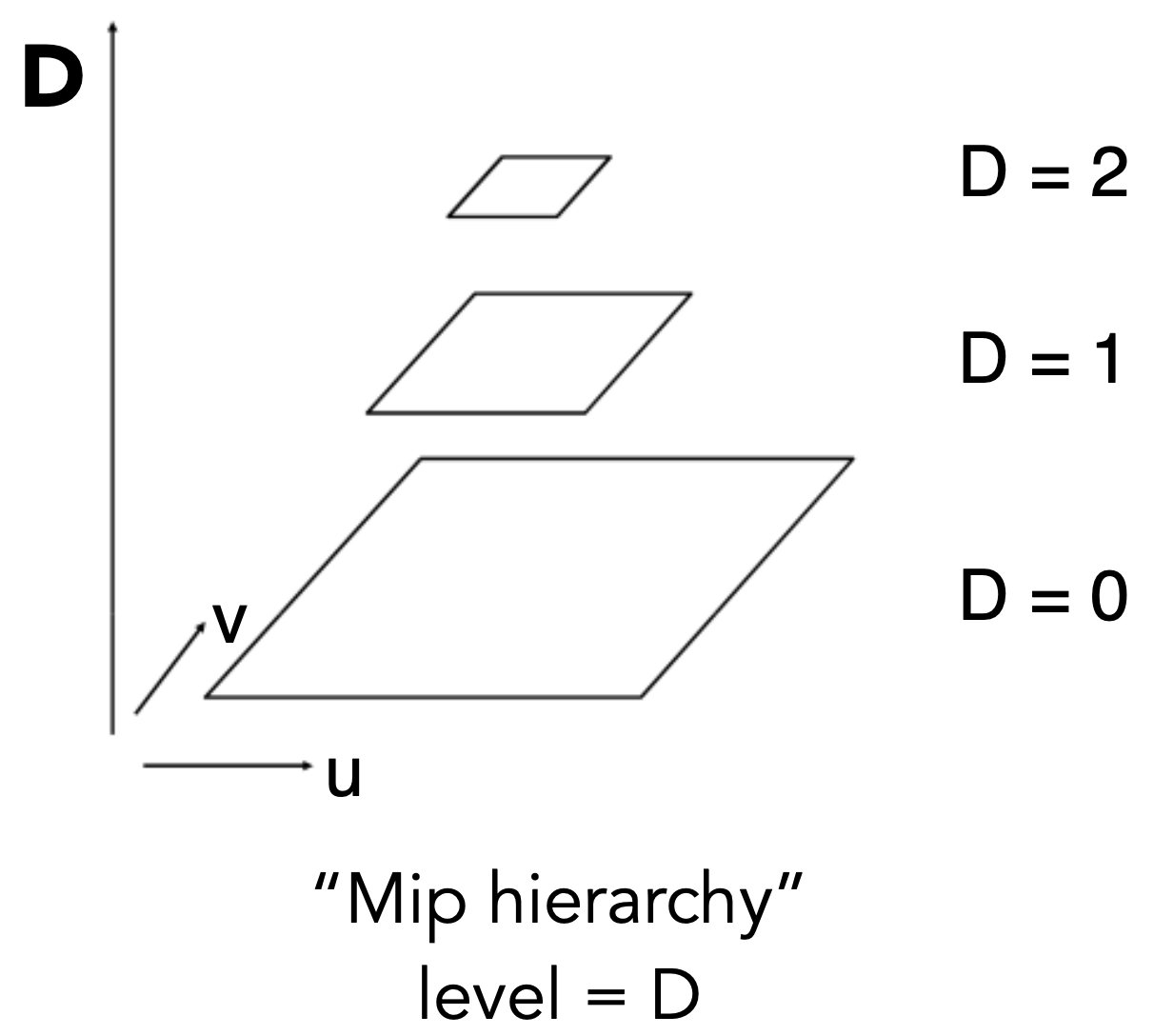
考虑到一个正方形的纹理图片 $n \times n$，当缩小分辨率时，其增加的存储空间有多少？估算一下：

$$
n \times n + \frac{1}{2}n \times \frac{1}{2}n + \frac{1}{2^2}n \times \frac{1}{2^2}n + \frac{1}{2^3}n \times \frac{1}{2^3}n + \cdots = \frac{1 \times (1 - \frac{1}{4^{\infty}})}{1 - \frac{1}{4}} n \times n = \frac{4}{3} n \times n
$$

即，存储空间仅增加了原来的33%。

应用Mipmap

在应用Mipmop的过程中，需要两个步骤：

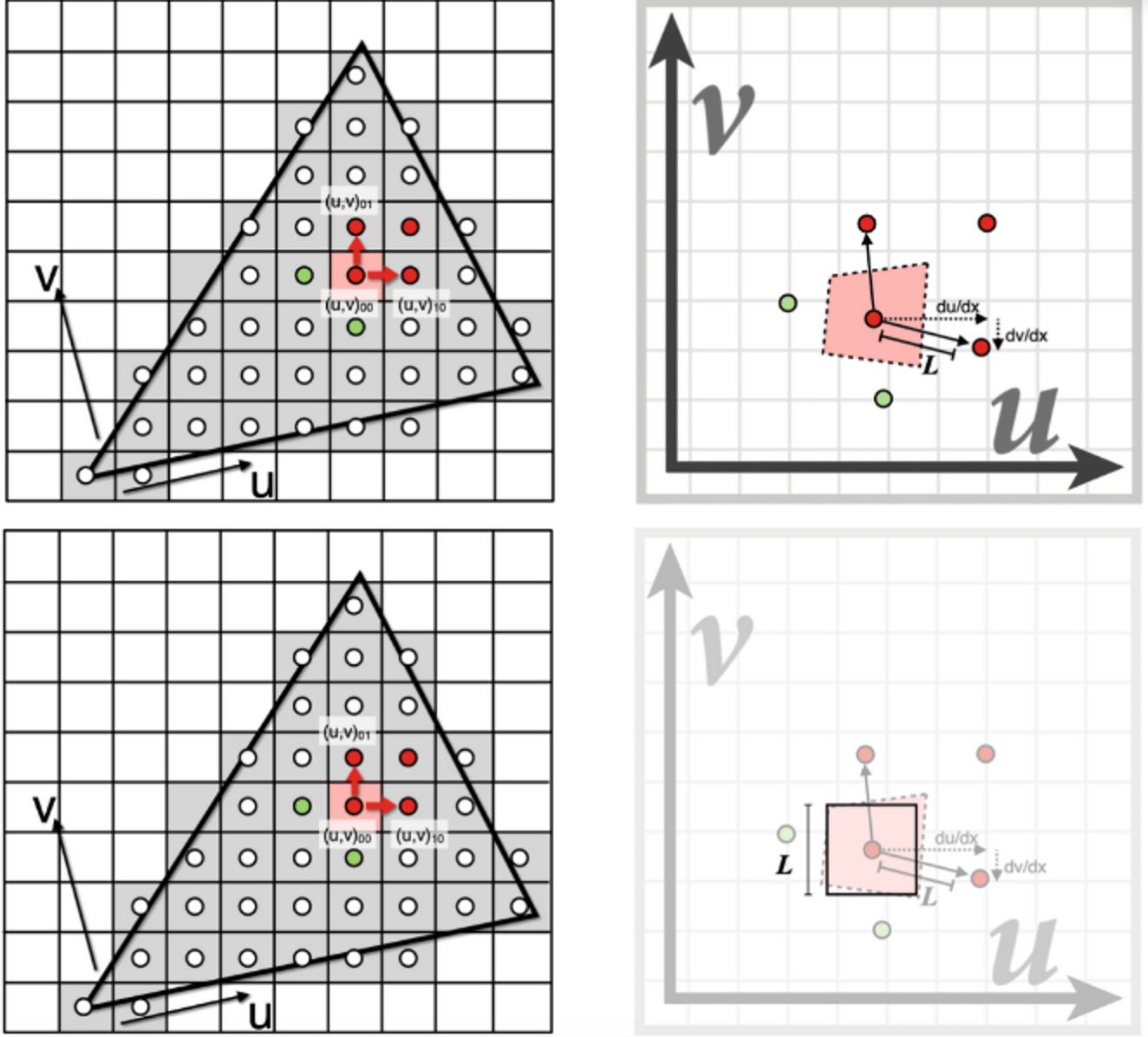
1. 首先要估算一个像素在纹理上的覆盖的区域大小；

   Estimate texture footprint using texture coordinates of neighboring screen samples.

   $$
   L=\max \left(\sqrt{\left(\frac{d u}{d x}\right)^{2}+\left(\frac{d v}{d x}\right)^{2}}, \sqrt{\left(\frac{d u}{d y}\right)^{2}+\left(\frac{d v}{d y}\right)^{2}}\right)
   $$ 实际计算中，也可以利用别的方法进行估计，如：直接利用像素点边界上的4个顶点进行估算。
2. 计算该纹理区域大小对应的纹理信息的平均值； 根据得到的覆盖范围 $L$，确定了正方形的大致范围。然后查询该覆盖范围对应的平均纹理信息： $$
   D = \log_2 L
   $$

   D rounded to nearest integer level.

   其中 D对应的是mipmap中的不同层中经过分辨率缩小的纹理图片。

Mipmap分层带来的不连续问题

利用该方法发现，不同层之间是离散的，因此当“贴”到物体上时，会出现明显的界限，

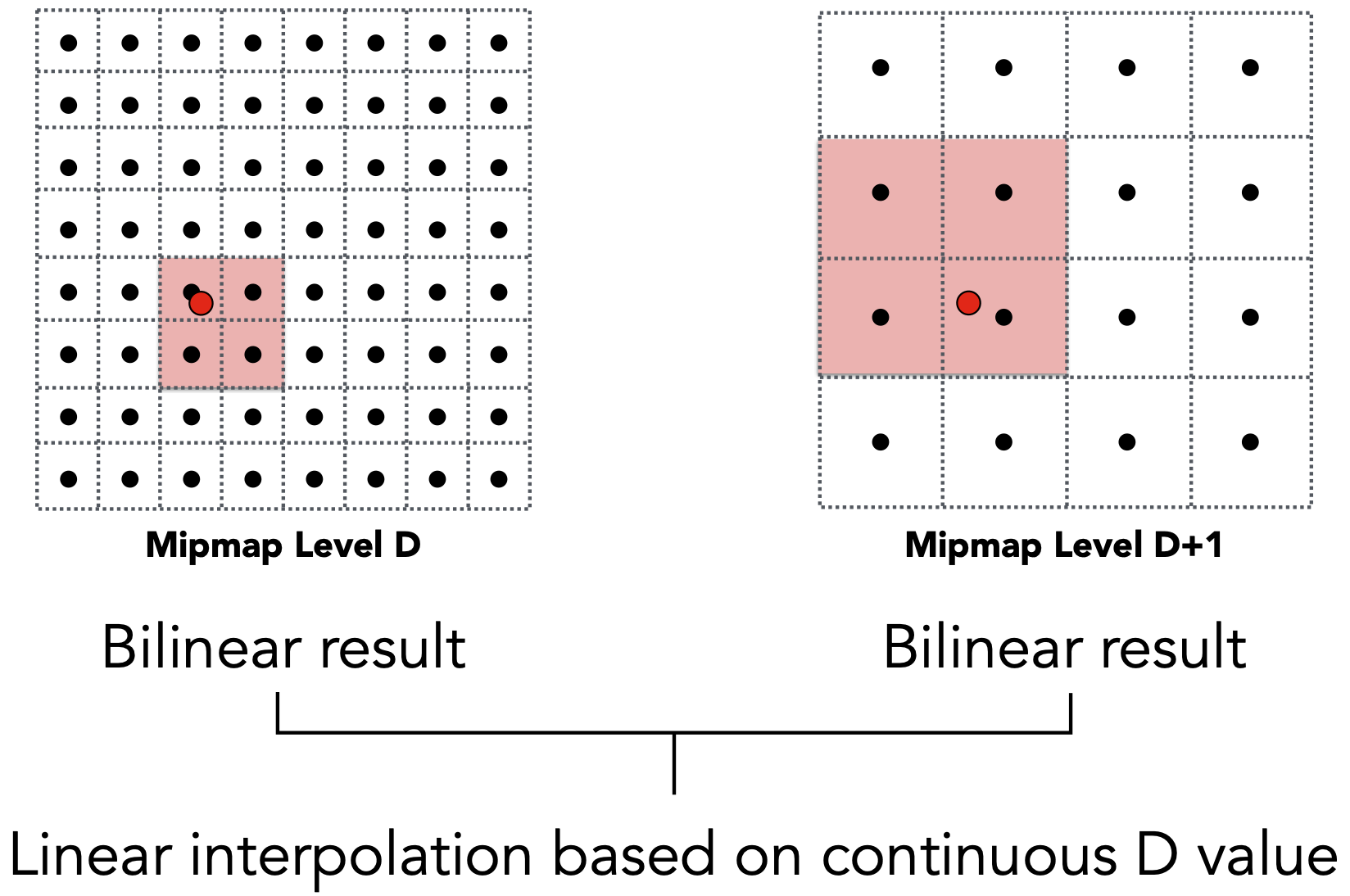
为了平滑过度，需要将不同层的纹理图片之间建立连续的关系——插值。

复用之前的bilinear方法，相比于之前，这些还需要在不同层之间进行插值，因此称之为——Trilinear Interpolation。

Mipmap的缺陷

Mipmap方法的效果如下：

发现Mipmap相比于Point sampling能够解决部分问题，但是相比于利用MSAA方法，在远处出现了overblur。主要的原因在于mipmop只能处理正方向区域的近似范围查询，但是在上图中显然在远处，会有一些矩形出现，因此用一个正方形覆盖矩形，难免会出现平滑过度的问题，因此远处连成一片了。

针对不规则区域映射的问题：

• mipmop只能解决正方形区域近似范围计算的问题；
• Anisotropic Filtering则同时能够对矩形进行范围计算；
• EWA filtering能进一步对不规则放置的四边形进行范围计算；

解决方案3：Range Query - Anisotropic Filtering

解决问题

Can look up axis-aligned rectangular zones.

限制

Diagonal footprints still a problem.

该方法将存储空间提高了3倍：

$$
n \times n + 2 \times \left( \frac{1}{2}n \times n + \frac{1}{2^2}n \times n + \frac{1}{2^3}n \times n + \cdots \right) = n \times n + 2 \times \frac{\frac{1}{2} \times (1 - \frac{1}{2^{\infty}})}{1 - \frac{1}{2}} n \times n = 3 n \times n
$$

解决方案4：Range Query - EWA filtering

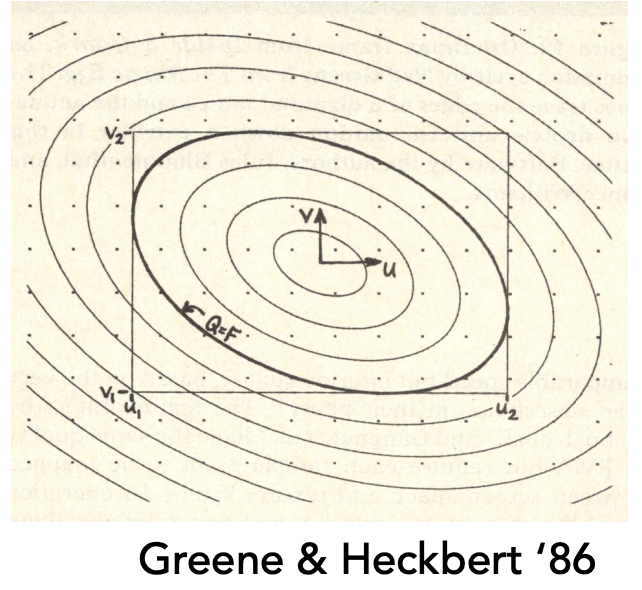
idea

• Use multiple lookups：同时使用多个图形近似计算不规则区域；
• Weighted average：对多个图形进行加权计算；
• Mipmap hierarchy still helps

解决问题

• Can handle irregular footprints