Texture的泛化理解
泛化理解texture:In modern GPUs, texture = memory + range query (filtering)
即,纹理不仅仅用在图像上,可以是任意的内存数据和对应的范围查询方法。
基于这种理解,texture其实是:
General method to bring data to fragment calculations.
可以在很多的场景中使用:
- Environment lighting
- Store microgeometry
- Procedural textures
- Solid modeling
- Volume rendering
Environment lighting
对于在着色模型中,将环境光视为常数,与其他两项相加共同完成着色过程。通过纹理可以记录环境光,然后应用到任意的渲染物体上,这种方法比之前应用点光源的效果要好很多。
例子:Environment Map

假设
用纹理描述环境光时,假设所有光照均来自无限远处。这种假设使得光照均来自同一个方向,即光照方向的不同不会对环境光的记录产生影响。
记录环境光
Spherical Environment Map
将环境光照存储在球面上,然后将其展开,之后贴到不同的物体上。但是这种方法在靠近球的极点的位置上,会出现扭曲的现象。


解决方法:Cube Map
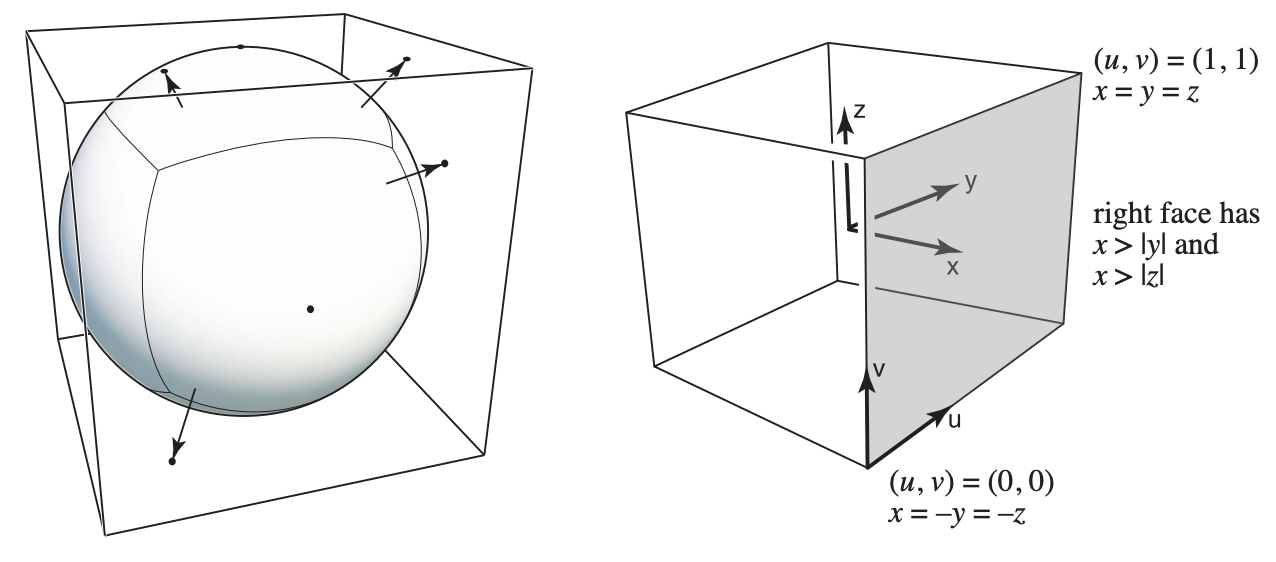
A vector maps to cube point along that direction.
The cube is textured with 6 square texture maps.
简单来说,在球体外切一个立方体,然后将通过球体记录的信息映射到该立方体中。
这种方法:
- 使得扭曲现象得到缓解;
- 但是需要增加计算:需要找到球面上的方向信息映射到立方体的哪个面上;

Store microgeometry
纹理不仅可以存储颜色信息,还可以用于存储几何信息。
Bump / Normal mapping
Idea
用于定义shading surface中的shading point的相对高度,从而实现“凹凸不平”的效果,但是这种实现并没有改变原本的几何形状,而是Fake the detailed geometry。
这种方法的好处在于:
- 没有改变几何物体形状,但是通过复杂的纹理可以实现相同的目标。
Adding surface detail without adding more triangles
其核心idea在于:
- Perturb surface normal per pixel (for shading computations only)
- “Height shift” per texel defined by a texture
如何计算新的法线
基于这种想法,一个点的高度通过纹理信息被“修改”了,从而也修改了对应的法线信息。那么一个问题是:How to modify normal vector?
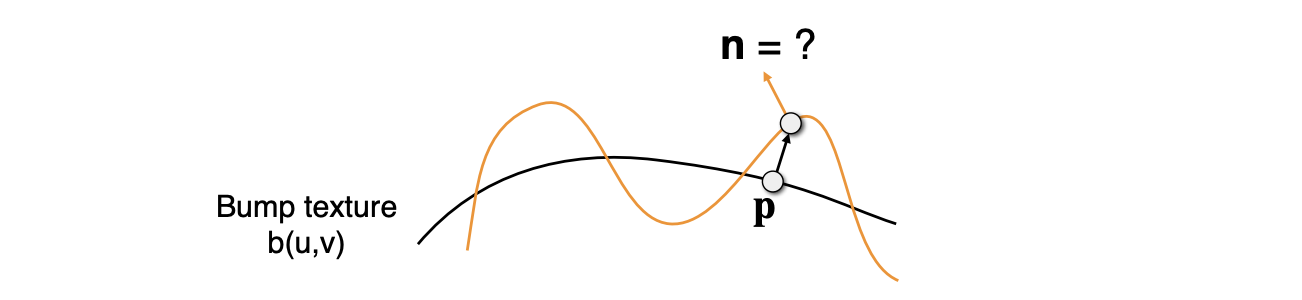
根据不同的应用场景,可以分为:
- in flatland (1D)
- 假设原始着色平面的法线向量沿着y轴方向 $n(p) = (0, 1)$;
- 对于加入纹理信息后,一个点p的相对高度发生变化,其导数方向为:每移动1,则高度变化为 $dp = c \cdot [h(p+1) - h(p)]$,因此导数方向为 $(1, -\text{dp})$,其中 $c$ 是放缩因子。
- 根据旋转变换,对应该点的法线向量为 $n(p) = (-dp, 1).\text{normalized}()$;
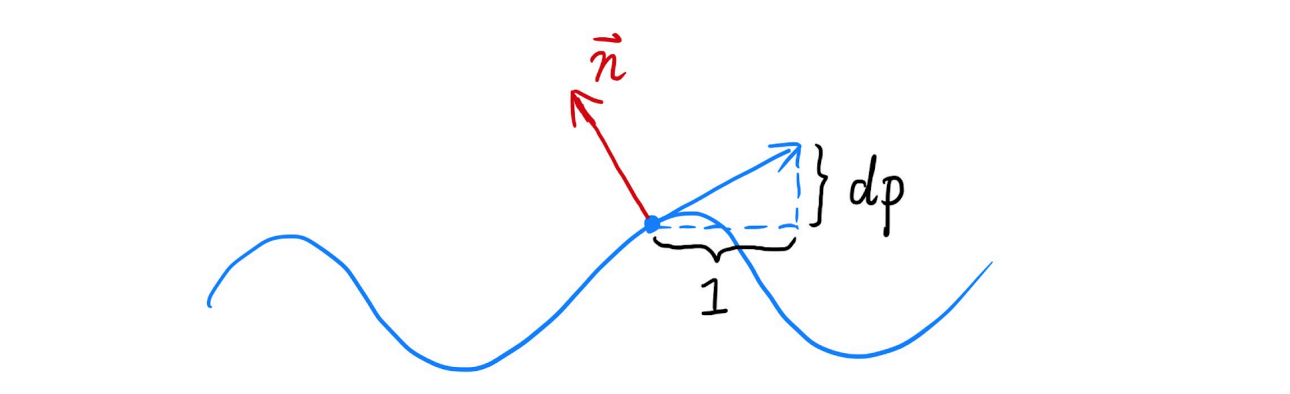
- in 3D 在真实的纹理中计算导数时,需要同时在纹理坐标的 $u,v$ 方向同时计算。 同样的过程:
- 假设原始着色平面的法线向量 $n(p) = (0,0, 1)$;
- p点在纹理上的导数方向: $$
\begin{array}{l}
dp / du= c_1 \cdot [h(\mathbf{u}+1)-h(\mathbf{u})] \\
dp / dv=c_2 \cdot [h(\mathbf{v}+1)-h(\mathbf{v})]\end{array}
$$ - 最终新的法线方向为:$n = (-dp/du, -dp/dv, 1).\text{normalized}()$
在该过程中所有的向量计算均针对的是local coordinate,因此为了应用需要将该坐标变换到真实世界中的坐标中。
Displacement mapping
Idea
- a more advanced approach
- Uses the same texture as in bumping mapping
- Actually moves the vertices:相比于bumping mapping不改变几何形状,这里的方法是将shading point进行移动,而不是虚拟操作。两种方法的效果对比如下:
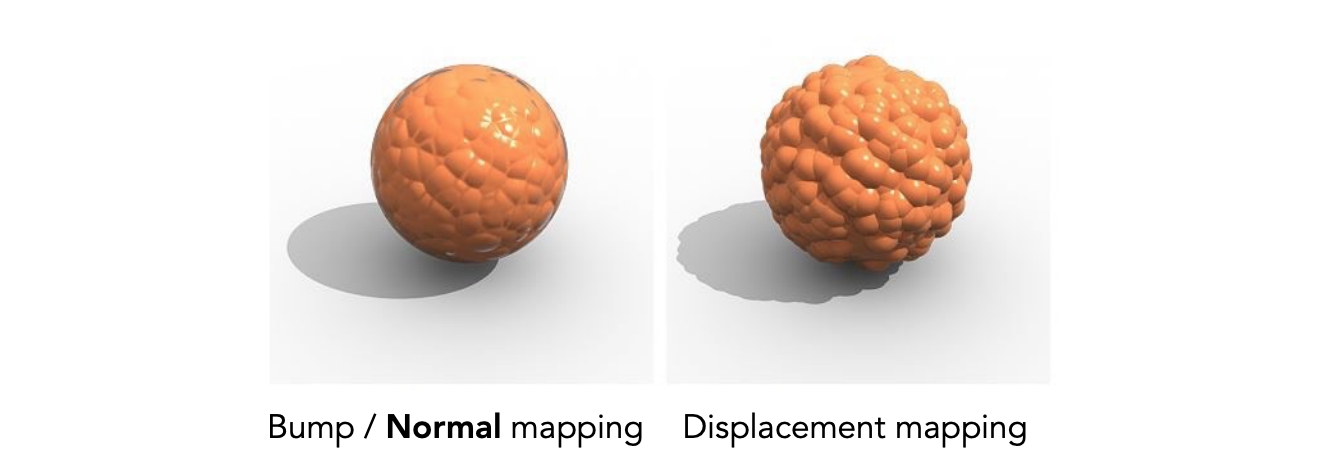
代价
- 要求几何形状中的三角形足够密集、细致:这样对于不同的纹理图片中调整的高度,待渲染对象中的三角形不会因为过大出现走样问题;
一种优化方法
- 当三角形不够细致时,可以动态检测三角形是否应该更小和细致?在Direct X中可以动态调整三角形的细致程度。

