Explicit Representations
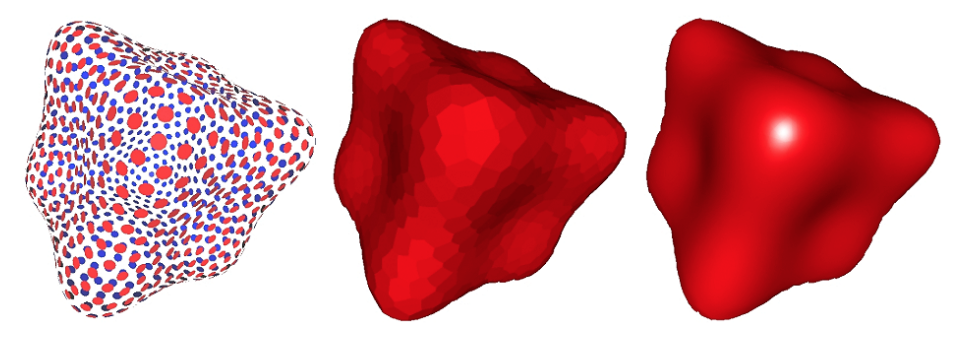
Point Cloud
- Easiest representation: list of points $(x,y,z)$
- 不直接对几何表面进行表示,而是对构成图形的点的集合进行表示;
- Easily represent any kind of geometry
- 只要点足够多和密集,就能够表示任意的几何物体;
- Useful for LARGE datasets (>>1 point/pixel)
- Often converted into polygon mesh
- Difficult to draw in undersampled regions
- 当点不够密集时,则无法构成平面;
Polygon Mesh
- Perhaps most common representation in graphics
- 最广泛的应用
- Store vertices & polygons (often triangles or quads)
- Easier to do processing / simulation, adaptive sampling
- More complicated data structures

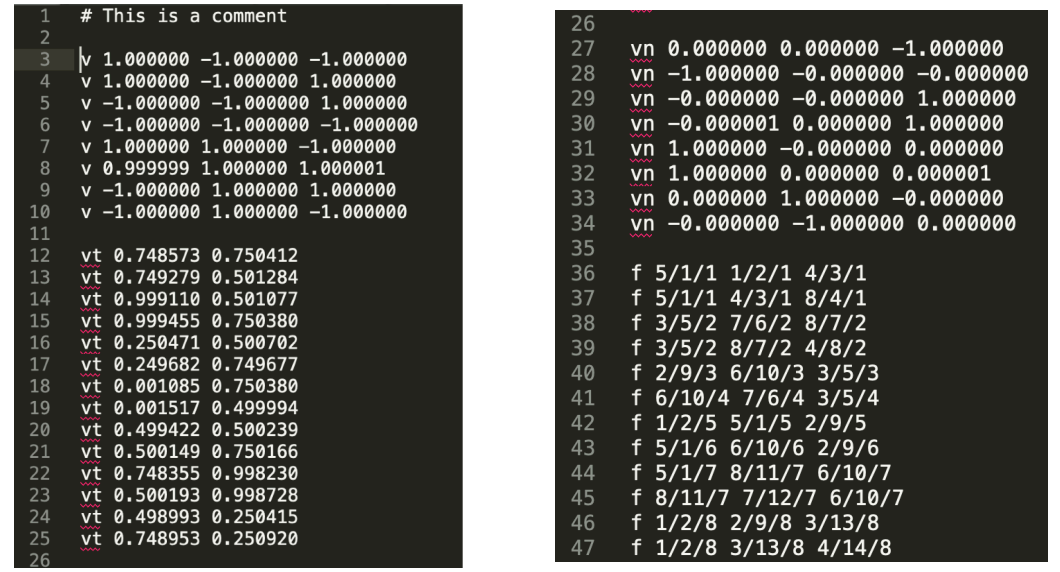
The Wavefront Object File (.obj) Format
- 该文件格式用于表示三角形面形成的物体
- Just a text file that specifies vertices, normals, texture coordinates and their connectivities
- 其中:
- v:表示顶点向量;
- vt:表示纹理坐标;
- vn:表示顶点的法线向量;
- f:表示三角形的各个面,以及它们之间的连接关系,其中三个序号依次为:顶点向量、纹理坐标、法线向量;
- 例如:5/1/1 1/2/1 4/3/1 表示第5、1、4个顶点构成三角形,每个顶点对应的纹理坐标对应第1、2、3个,法线向量对应1、1、1个。
Bézier Curves
这是一种对于曲线显式表示的方法。
Idea
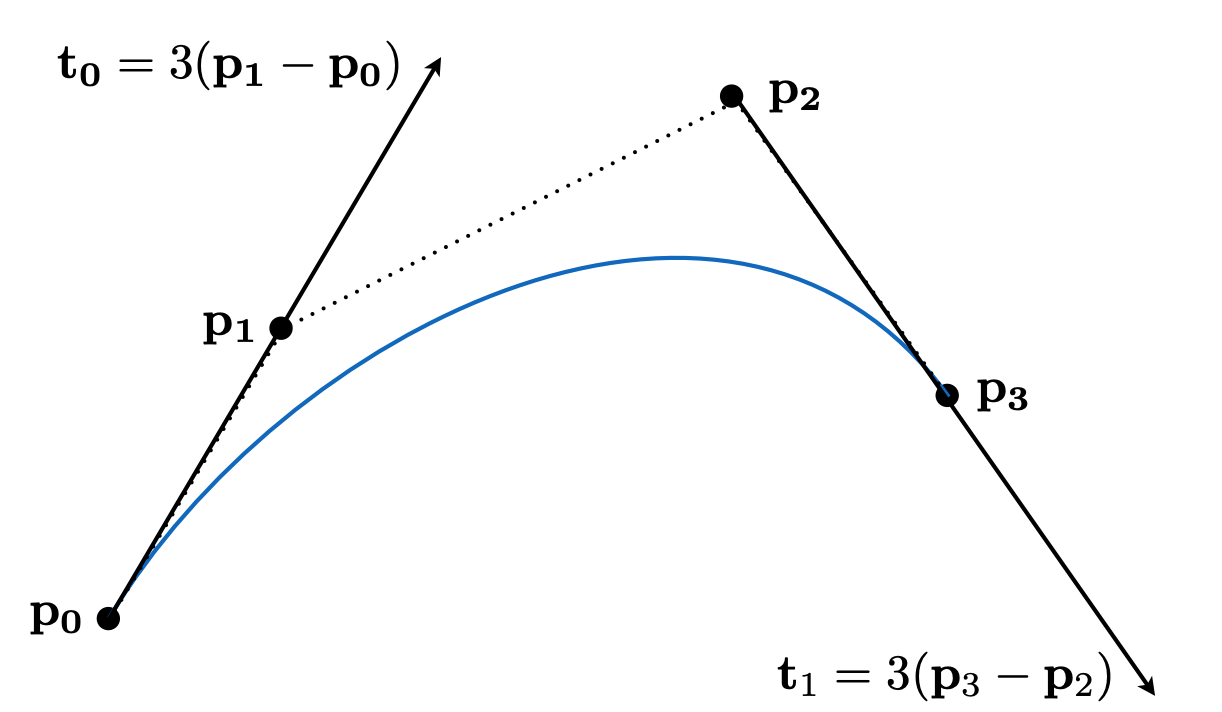
用一系列的控制点来表示曲线,以满足其特定的性质。
其中:
- 控制点能唯一确定一条曲线;
- 但是不要求曲线能经过控制点,曲线只需要经过起点和终点;
绘制Bézier Curves
问题
如果利用任意多个控制点,绘制一条Bézier Curves?
解决方法:de Casteljau Algorithm
该算法可以利用控制点生成曲线,其本质是在不同的线段上进行插值,然后将所有的插值点视为基础点,不断递归,直到最终的结果中只有一个插值点,该插值点即在生成的曲线上。
为了理解这个算法的过程,下边从:
- 几何角度;
- 代数角度;
两个方面理解这个算法。
几何角度
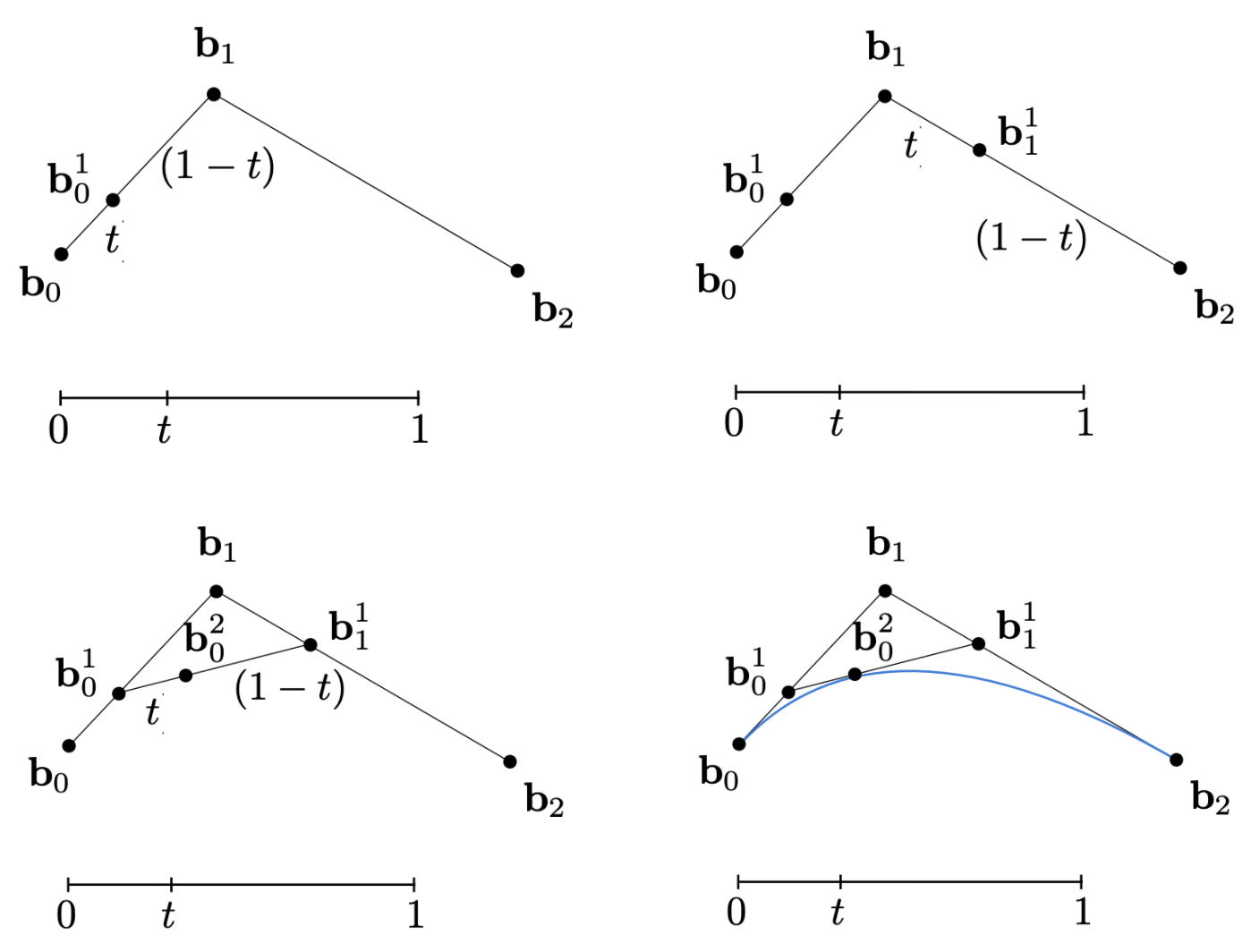
为了说明,考虑有三个控制点的情况(这种情况下生成的曲线称为quadratic Bezier)。
在如下3个控制点中,$\bf{b}_0$、$\bf{b}_2$ 分别为起点和终点,$\bf{b}_1$ 确定曲线的弯曲方向。那么如何控制曲线的生成呢?
一种方式是,为了从 $\bf{b}_0$ 到 $\bf{b}_2$ 绘制曲线,将从 $\bf{b}_0$ 开始的时间定为0,到 $\bf{b}_2$ 的时间定为1,那么曲线的绘制过程,其实就是找到在 $[0, 1]$ 时间范围内,曲线上的点的位置。因此,将绘制曲线的算法转换为定位一个点的位置的方法。
具体过程如下:
- Insert a point using linear interpolation 具体来说,即在$\bf{b}_0$、$\bf{b}_1$之间插值一个点 $\mathbf{b}_0^1$ ,使得: $$
\mathbf{b}_0^1 = (1 - t) \mathbf{b}_0 + t \bf{b}_1
$$ - Insert on both edges 使用同样的方式在$\bf{b}_1$、$\bf{b}_2$之间插值一个点 $\mathbf{b}_1^1$ ,使得: $$
\mathbf{b}_1^1 = (1 - t) \mathbf{b}_1 + t \bf{b}_2
$$ - Repeat recursively 按照上述方式进行递归计算,在$\mathbf{b}_0^1$ 和 $\mathbf{b}_1^1$两个插值点之间再进行插值得到新的插值点 $\mathbf{b}_0^2$ ,使得: $$
\mathbf{b}_0^2 = (1 - t) \mathbf{b}_0^1 + t \mathbf{b}_1^1
$$ 问题是:递归的结束条件是什么?当插值点只有一个时,即完成了递归过程。如利用3个控制点生成曲线的过程中:- 第1次插值:得到2个插值点 $\mathbf{b}_0^1$ 和 $\mathbf{b}_1^1$;
- 第2次插值:得到1个插值点 $\mathbf{b}_0^2$ ;
- Run the same algorithm for every t in $[0,1]$ 对于范围$[0,1]$ 中的每个 $t_i$,均进行上述过程,即完成了曲线的绘制。
对于4个控制点生成曲线,过程如下:
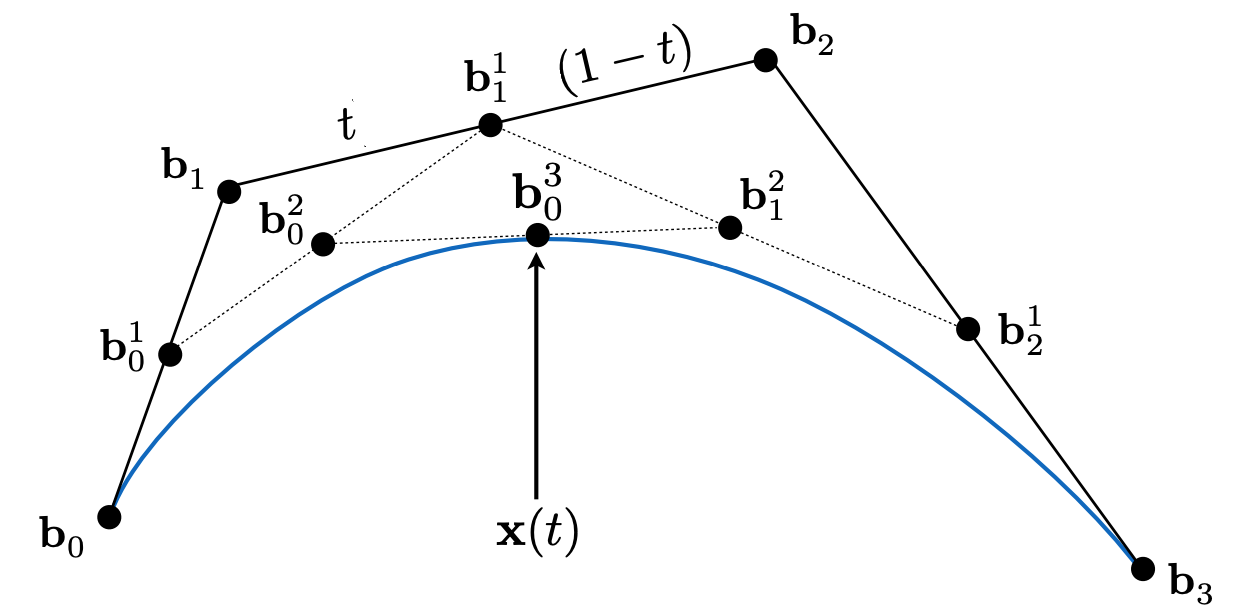
动画效果如下:
参考资料:Animation: Steven Wittens, Making Things with Maths, http://acko.net
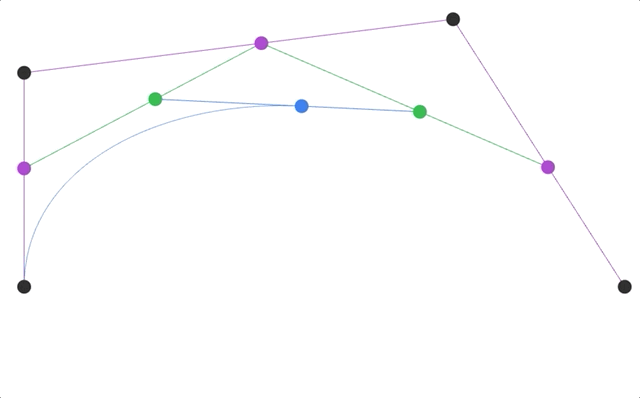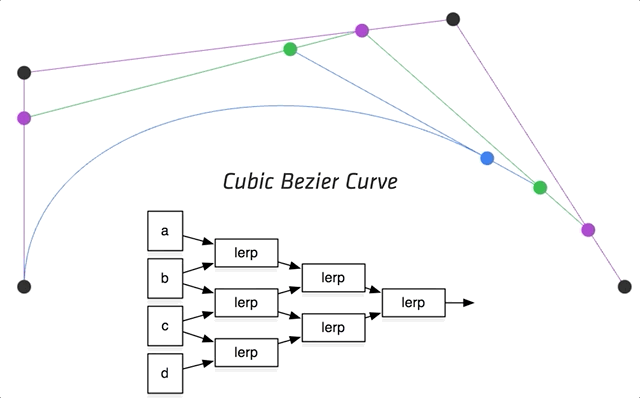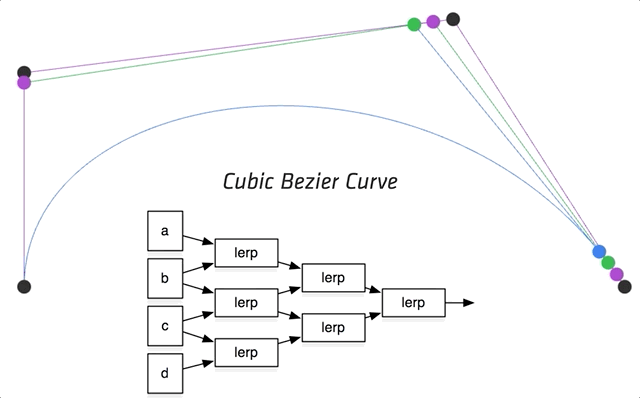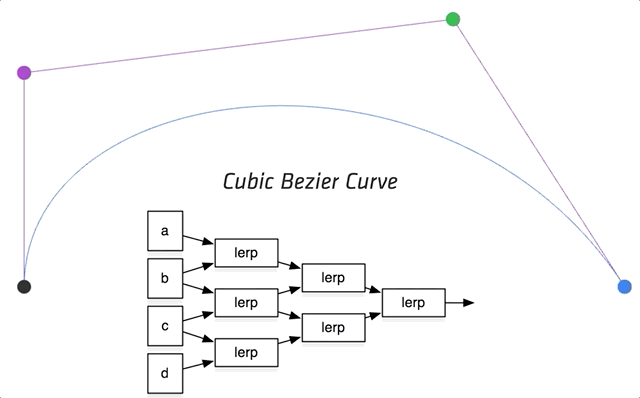
代数角度
在该算法中,通过对控制之间的线段不断进行插值,得以得到如下的金字塔形状。
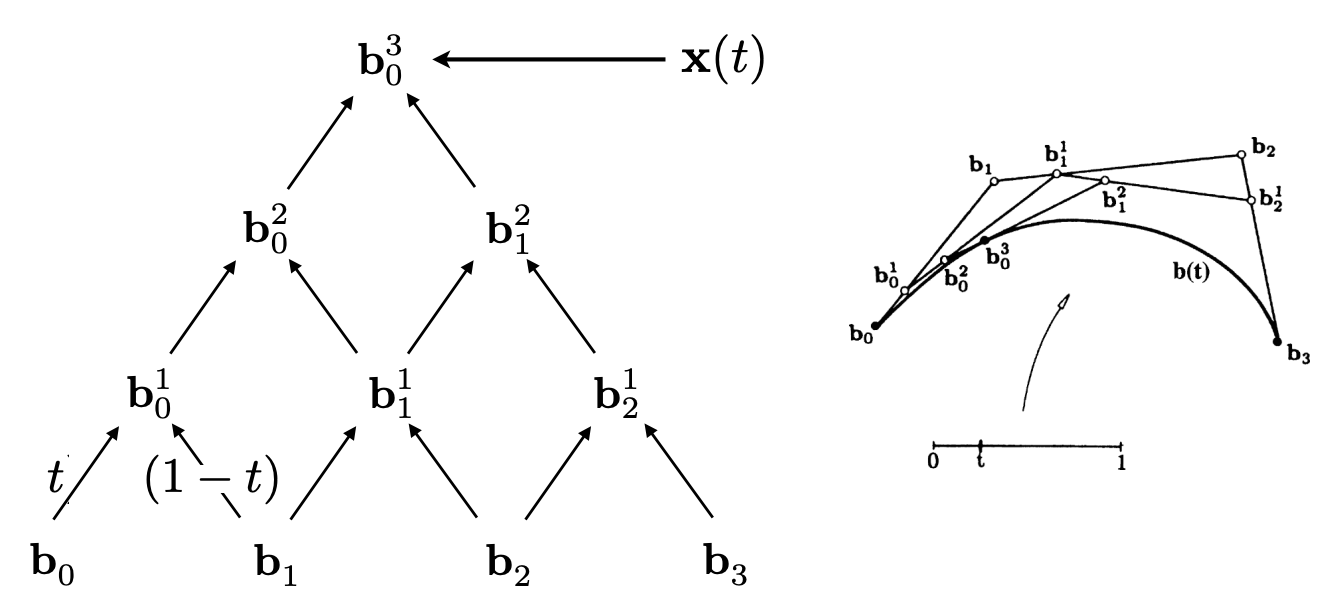
- Every rightward arrow is multiplication by $t$ ;
- Every leftward arrow by $(1–t)$ ;
对于3个控制点形成的贝塞尔曲线,可以得到:
$$
\begin{array}{l}
\mathbf{b}_0^1 (t)= (1-t) \mathbf{b}_0+t \mathbf{b}_1 \\
\mathbf{b}_1^1 (t)= (1-t) \mathbf{b}_1+t \mathbf{b}_2
\end{array}
$$
$$
\begin{array}{l}
\mathbf{b}_0^2(t) = (1 - t) \mathbf{b}_0^1 + t \mathbf{b}_1^1
\\
\mathbf{b}_0^2(t)=(1-t)^2 \mathbf{b}_0+2 t(1-t) \mathbf{b}_1+t^2 \mathbf{b}_2
\end{array}
$$
系数展开式
对于 $n+1$ 个控制点,可以进行 $n$ 次插值计算,其中生成的贝塞尔曲线上的任意一点均是控制点向量的线性组合,如下所示:
$$
\mathbf{b}^{n}(t)=\mathbf{b}_{0}^{n}(t)= \sum_{j=0}^n \mathbf{b}_j B_j^n (t)
$$
其中:
- $\mathbf{b}^{n}(t)$ : Bézier curve order $n$ (vector polynomial of degree $n$);
- $\mathbf{b}_{j}$ : Bézier control points (vector in $\mathbf{R}^N$);
- $B_{j}^{n}(t)$ : Bernstein polynomial (scalar polynomial of degree $n$);
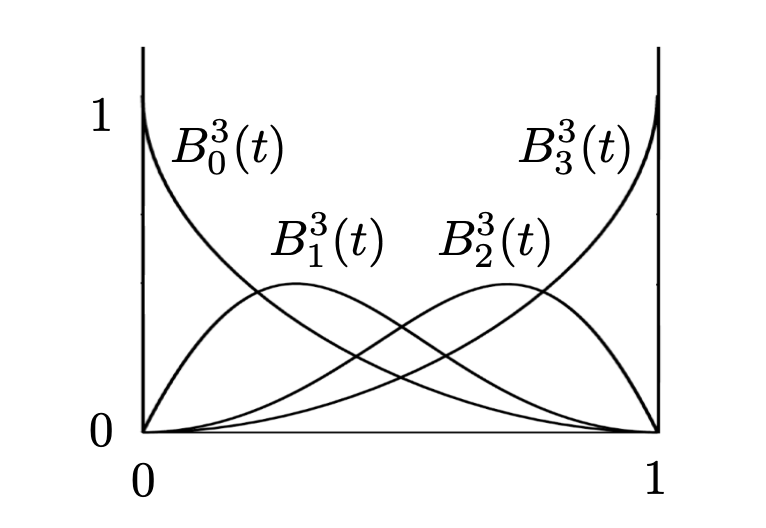
该线性组合的系数 $B_{j}^{n}(t)$ 是一个与时间 $t$ 有关的多项式,称之为Bernstein polynomial,如下:
$$
B_{i}^{n}(t)=\left(\begin{array}{l}n \\ i\end{array}\right) t^{i}(1-t)^{n-i}
$$
整个Bernstein polynomial其实是一个二项分布,因此对于任意的n次展开式,其所有对应的系数之和为1。
其中,控制点不一定是2D的,也可以是3D空间中的,例如对于4个3D的控制点如下:
$$
\mathbf{b}_0=(0,2,3), \mathbf{b}_1=(2,3,5), \mathbf{b}_2=(6,7,9), \mathbf{b}_3=(3,4,5)
$$
可以得知任意时间 t 下,对应的曲线上的点为:
$$
\mathbf{b}^n (t)=\mathbf{b}_0 (1-t)^3 +\mathbf{b}_1 3 t(1-t)^2 +\mathbf{b}_2 3 t^2 (1-t)+\mathbf{b}_3 t^3
$$
Bézier Curves的性质
- Interpolates endpoints 对于4个控制点(cubic Bézier),则有: $$
\mathbf{b}(0)=\mathbf{b}_0 ; \quad \mathbf{b}(1)=\mathbf{b}_3
$$ - Tangent to end segments 对于4个控制点(cubic Bézier),则有: $$
\mathbf{b}^{\prime}(0)=3\left(\mathbf{b}_1 -\mathbf{b}_0 \right) ; \quad \mathbf{b}^{\prime}(1)=3\left(\mathbf{b}_3 -\mathbf{b}_2 \right)
$$ - Affine transformation property
对于贝塞尔曲线中的每个点进行仿射变换得到的贝塞尔曲线,与对贝塞尔曲线的控制点进行仿射变换然后再生成的贝塞尔曲线一致。因此,若要对贝塞尔曲线进行仿射变换,只需要对其控制点进行变换即可,然后再生成曲线。 这个性质只针对仿射变换,在投影等变换下不成立。Transform curve by transforming control points.
- Convex hull property 凸包性质
Curve is within convex hull of control points.
Piecewise Bézier Curves
问题
Higher-Order Bézier Curves会导致一些问题:
- 当控制点很多时,很难针对特定控制点操作,以控制整体曲线的形状;
解决方法
idea
- 不用控制点生成一条完整的曲线;
- 代替,使用少量的控制点生成一段曲线,然后将所有的曲线拼接起来;
chain many low-order Bézier curve
具体方法
Piecewise cubic Bézier the most common technique
即,实践中常用4个控制点生成一段曲线。

参考资料:Bezier Curve Demos
问题:如何保证曲线光滑连接
保证上一条曲线终点的导数与下一条曲线起点的导数相同,包括方向和大小。
在这个问题上,可以有两种类型的连续(Continuity):
- $C^0$ continuity:只要保证几何图形上连接即可; $$
\mathbf{a}_n = \mathbf{b}_0
$$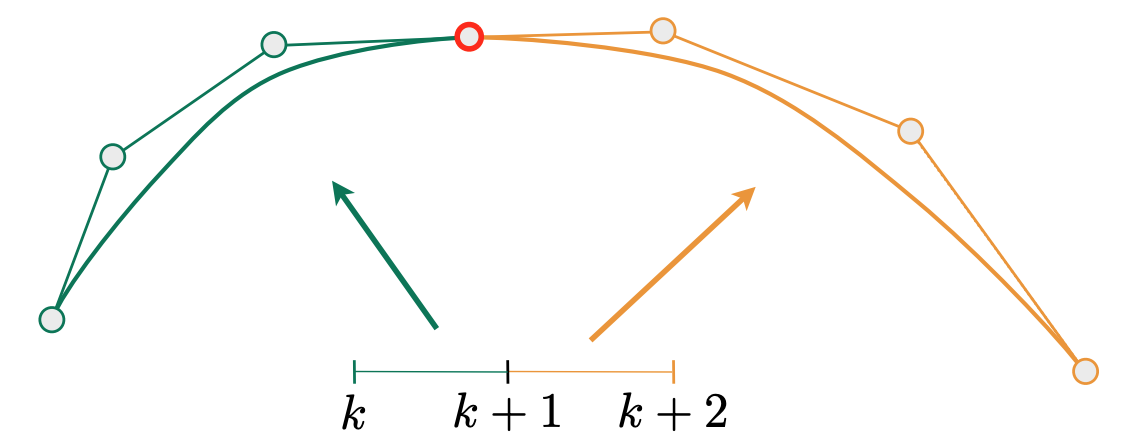
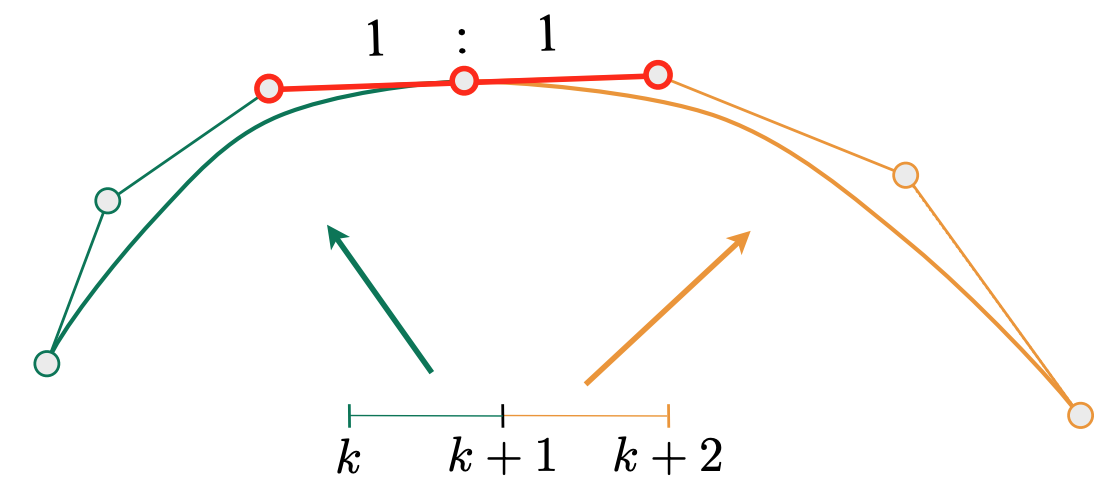
- $C^1$ continuity:不仅几何上连接,导数也要相同; $$
\mathbf{a}_n = \mathbf{b}_0 = \frac{1}{2} (\mathbf{a}_{n-1} + \mathbf{b}_1)
$$
在一些更严格的场合中,还有要求 $C^2$ continuity,即二阶导数相同。
Splines
a continuous curve constructed so as to pass through a given set of points and have a certain number of continuous derivatives.
In short, a curve under control.
B-splines
- Short for basis splines
- Require more information than Bezier curves
- Satisfy all important properties that Bézier curves have (i.e. superset)
本课中未详述样条内容,具体内容可以进一步参考以下资料。

