Bézier Surfaces
Extend Bézier curves to surfaces.
例子

绘制Bézier Surfaces
例子
Bezier surface and 4 x 4 array of control points.
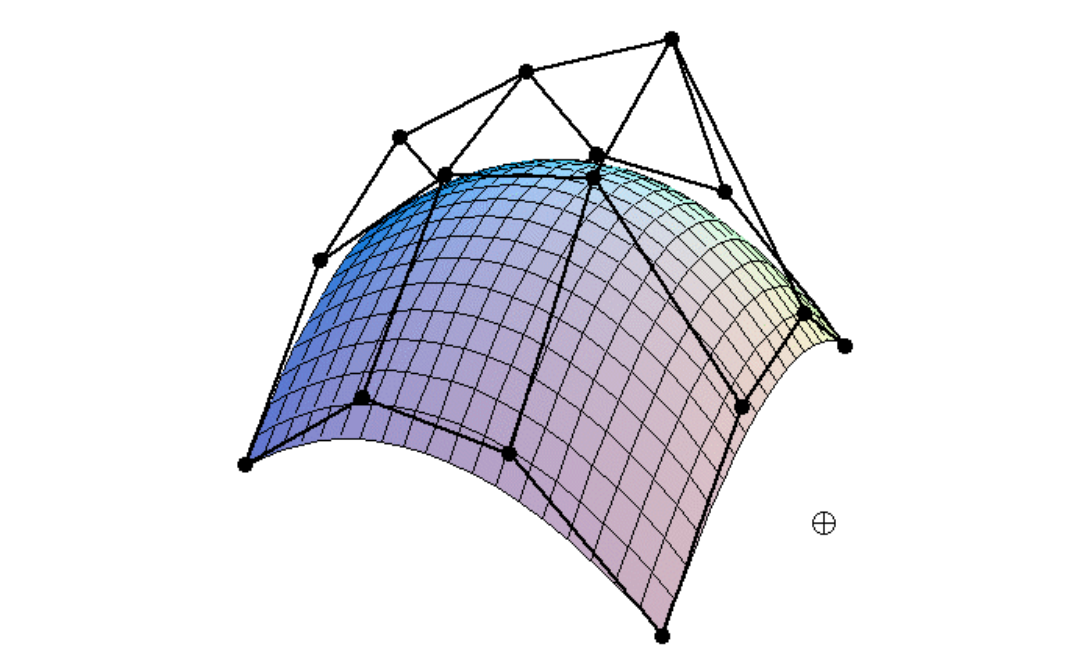
具体操作
以bi-cubic Bezier surface为例进行说明。
- 输入:$4 \times 4$ control points;
- 输出:2D surface parameterized by $(u,v)$ in $[0,1]^2$;
与Bézier curves同样的过程,只不过这里是在两个方向上进行双线性插值。
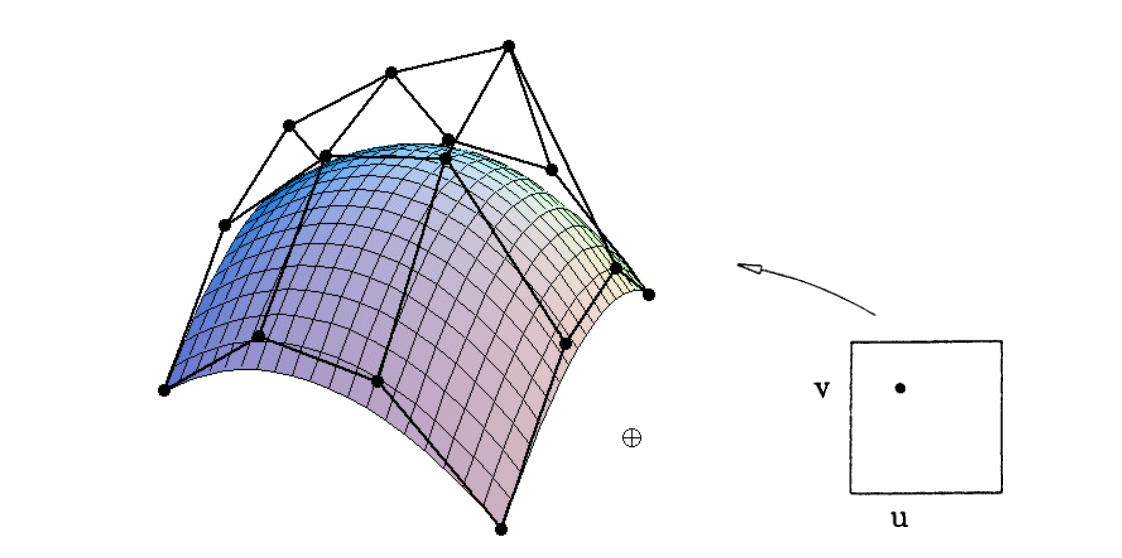
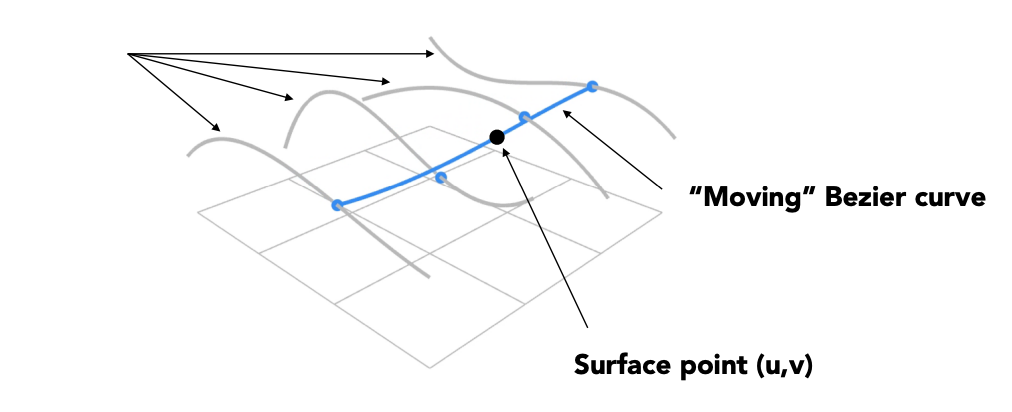
该方法称之为——Separable 1D de Casteljau Algorithm。由于在贝塞尔曲线的生成中,需要利用一个时间 $t$ 来生成对应的曲线,泛化到三维空间中,则需要两个时间来生成曲面,这里定义为 $u, v$。
具体过程如下:
- 首先,在时间 $u$ 方向上生成对应的贝塞尔曲线,这里定义使用 $4 \times 4$ 的控制点构建曲面,因此这一步需要生成4条对应的贝塞尔曲线,得到的结果是任意时间 $u_i$ 下的最终的插值结果。
- 将第一步得到的4个插值点视为 $v$ 方向上的控制点,然后再进行同样的插值操作,然后形成曲面上的一个点;
- 按照上述过程,不断递归,从而形成最终所有的曲面上的点。
动画效果如下:
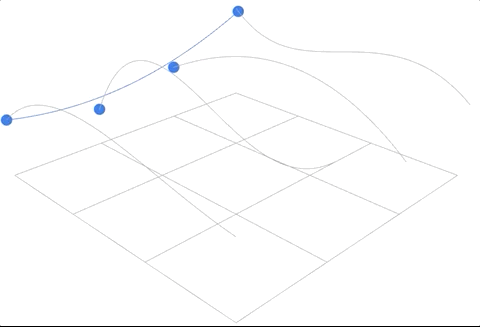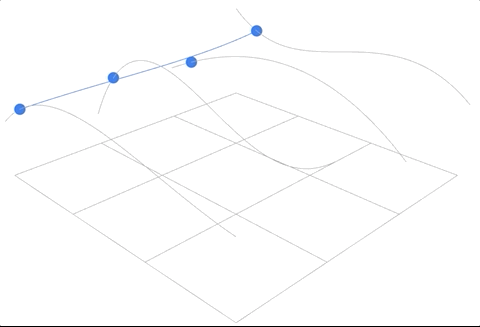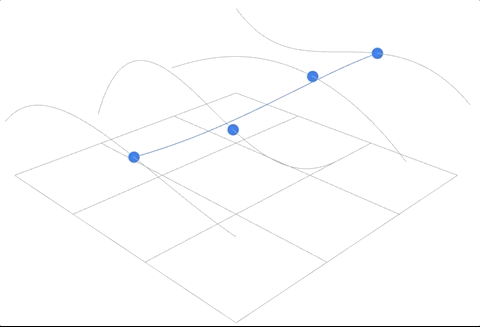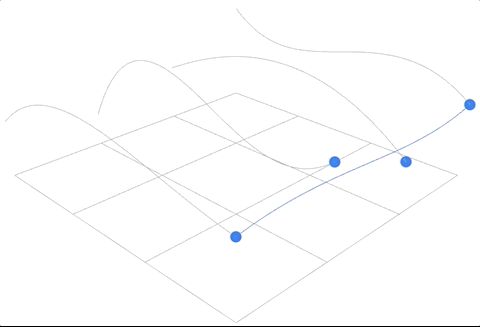
进一步阅读
这里类似之前在曲线中讨论的问题,如:
- 各个曲面如何拼接;
- 如果保证曲面拼接的“平滑”;
在曲线中遇到的问题在这里均会遇到,对于进一步的学习可以参考之前在曲线中提到的参考资料。

