介绍
前面提到很多几何图形的Explicit Representations,包括:
- triangle meshes
- Bezier curves & surfaces
- point clouds
虽然之前详述了Bezier curves & surfaces,但是在图形学中最常用的方式是Polygon Mesh,因为其有一些好的性质:
Easier to do processing / simulation, adaptive sampling
因此,Perhaps most common representation in graphics。
对于Mesh网络,其存在对应的几何操作:
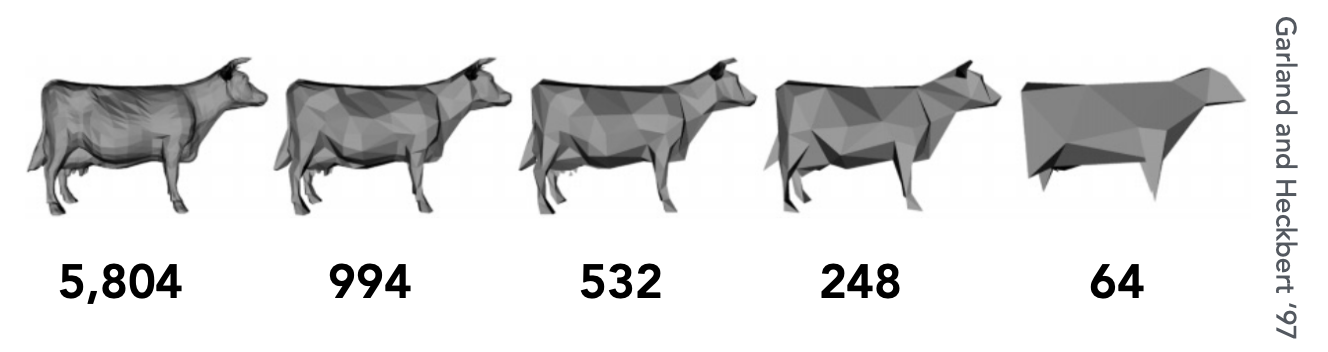
- Mesh subdivision(upsampling):细化三角形数量,实现了Increase resolution的效果;

- Mesh simplification(downsampling):正好与Mesh subdivision的效果相反;
Decrease resolution; try to preserve shape/appearance.

- Mesh regularization:使所有的三角形相同;
这种方式有利于解决因三角形大小不同导致的渲染困难等问题,在改善三角形表示的同时,不能损失模型的表示效果。Modify sample distribution to improve quality
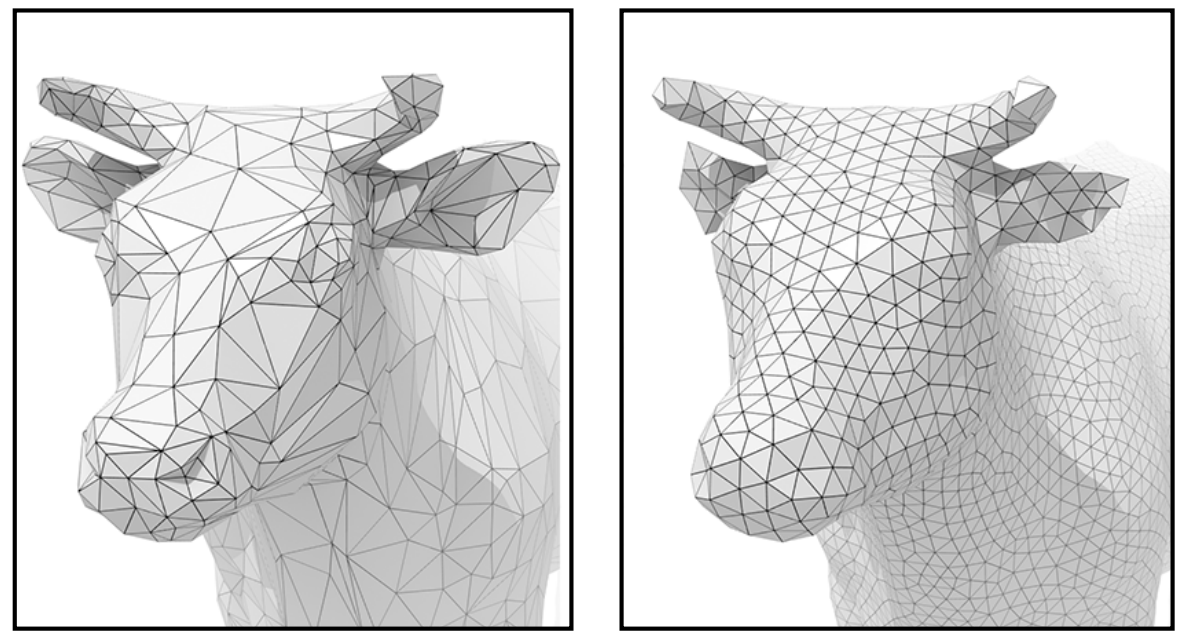
这一节主要是对Mesh的几何操作(Geometry Processing)进行说明。

Mesh Subdivision
含义
所谓的subdivision具体指两个操作:
- First, create more triangles (vertices)
- Second, tune their positions:使得几何形状更平滑;
这两步是 Common subdivision rule for triangle meshes。
方法1:Loop Subdivision
划分三角形
该方法只针对三角形,将每条边的中点连接从而形成4个三角形。
Split each triangle into four.

调整位置
完成三角形划分后,需要调整三角形顶点的位置。
Assign new vertex positions according to weights
对于新的顶点和旧的顶点采用不同的方法进行调整。
New / old vertices updated differently
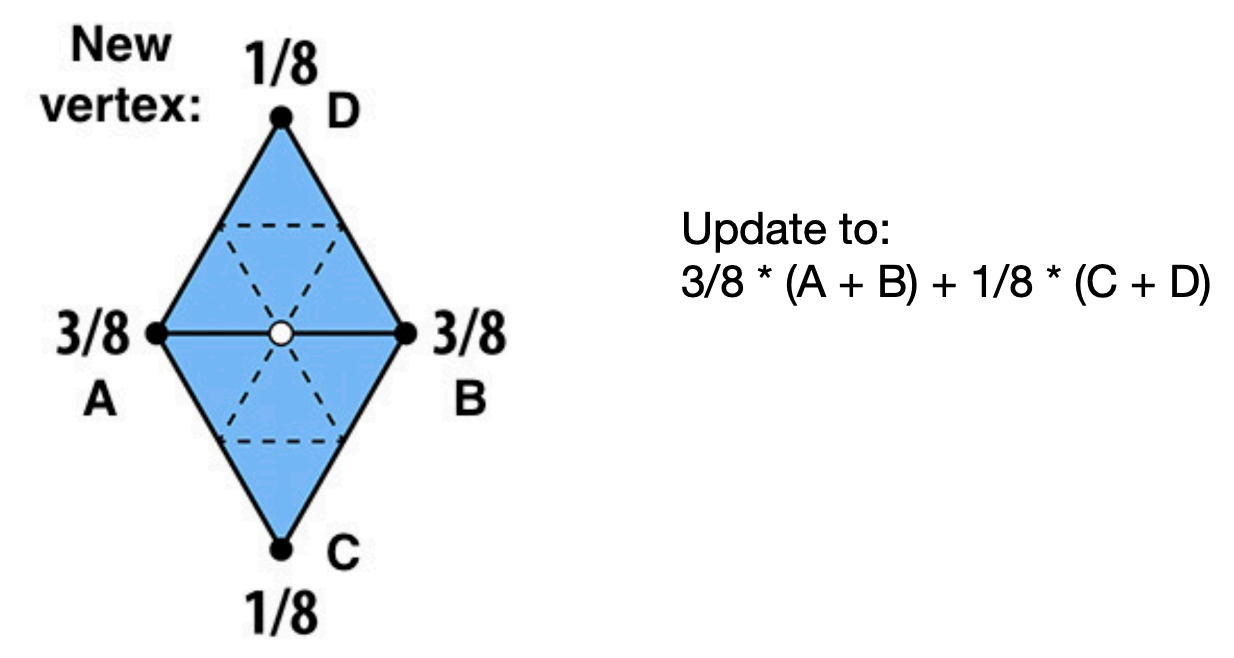
- 对新顶点:对中心的新顶点,其新的位置取决于周围的旧节点;
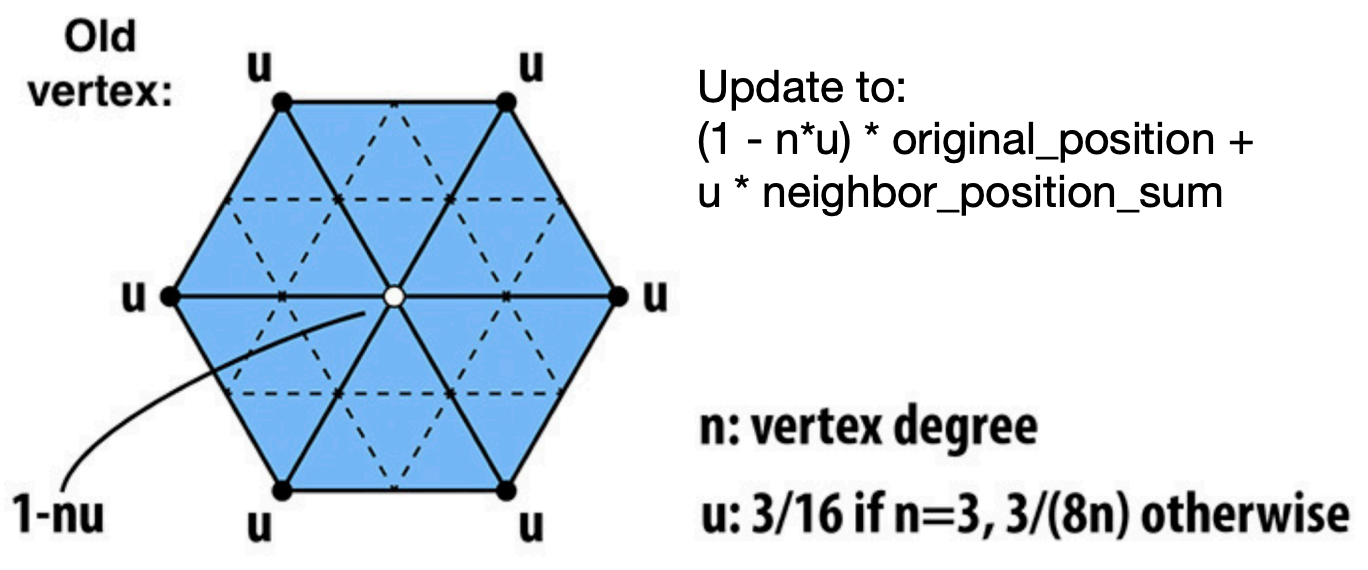
- 对旧节点:其新的位置取决于自己原来的位置,和其周围节点的位置。 对于一个节点来说,当其度很大的时候,其自身的影响可以忽略不计;当度很小的时候,其需要更多的考虑自身之前的节点位置。
方法效果
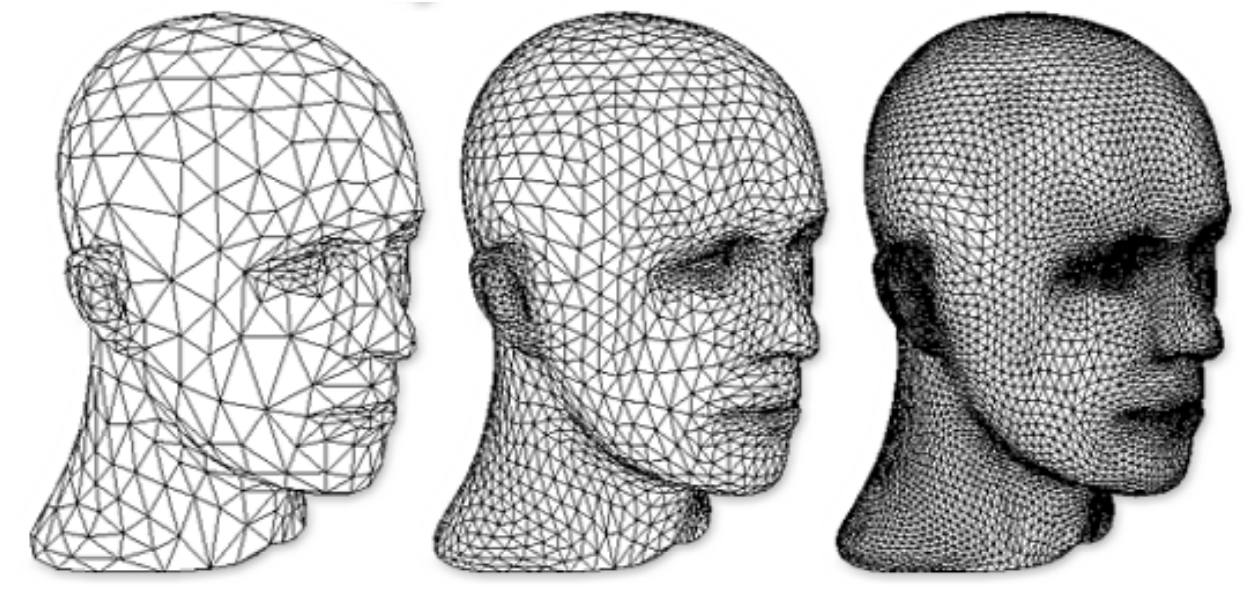
方法2:Catmull-Clark Subdivision
问题
Loop Subdivision只能针对网格中的三角形进行细分,无法作为通用的几何图形细分方法。
概念定义
- Non-quad face:不是四边形构成的面;
- Extraordinary vertex:顶点的度不为4(degree != 4) ;
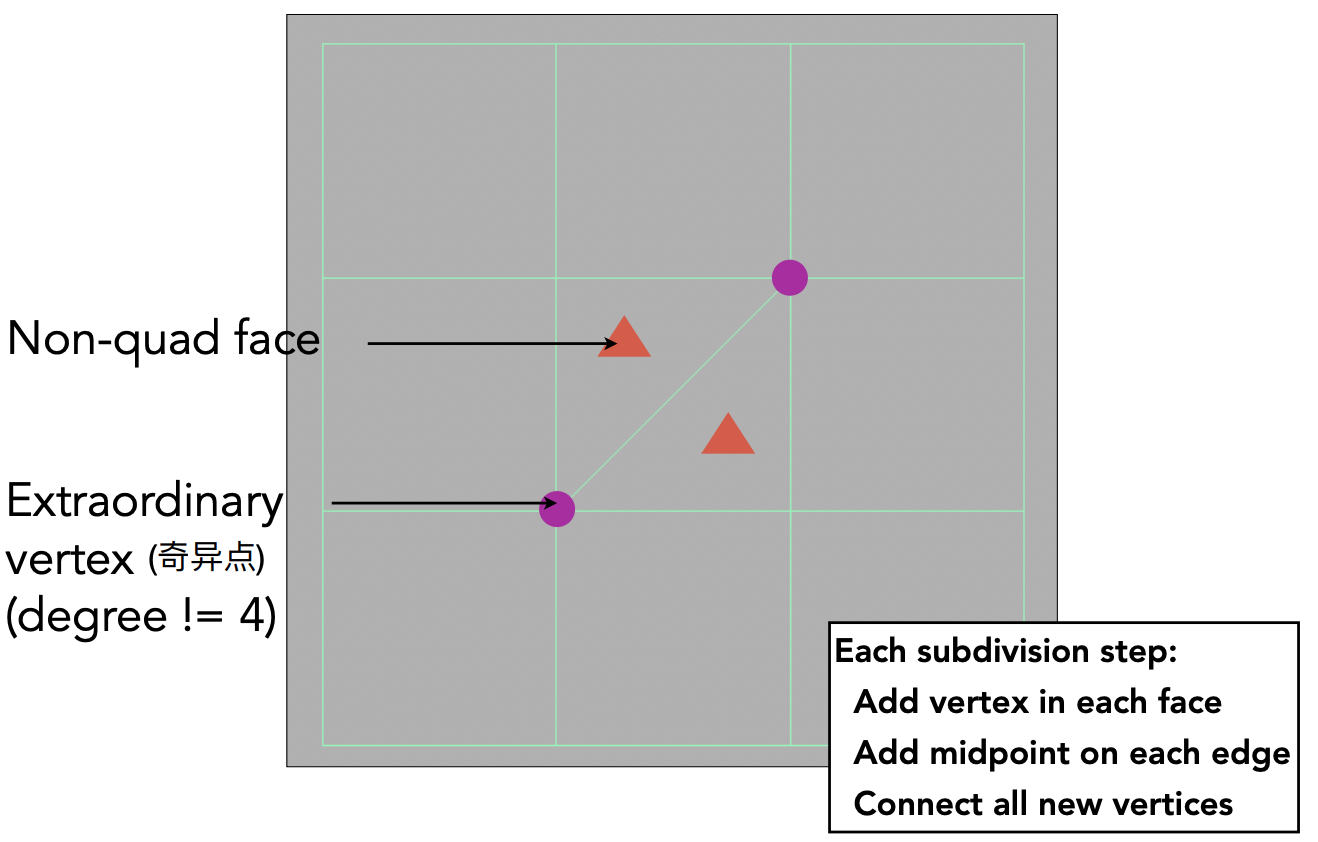
增加三角形
为了增加三角形,具体步骤如下:
- Add vertex in each face
- Add midpoint on each edge
- Connect all new vertices
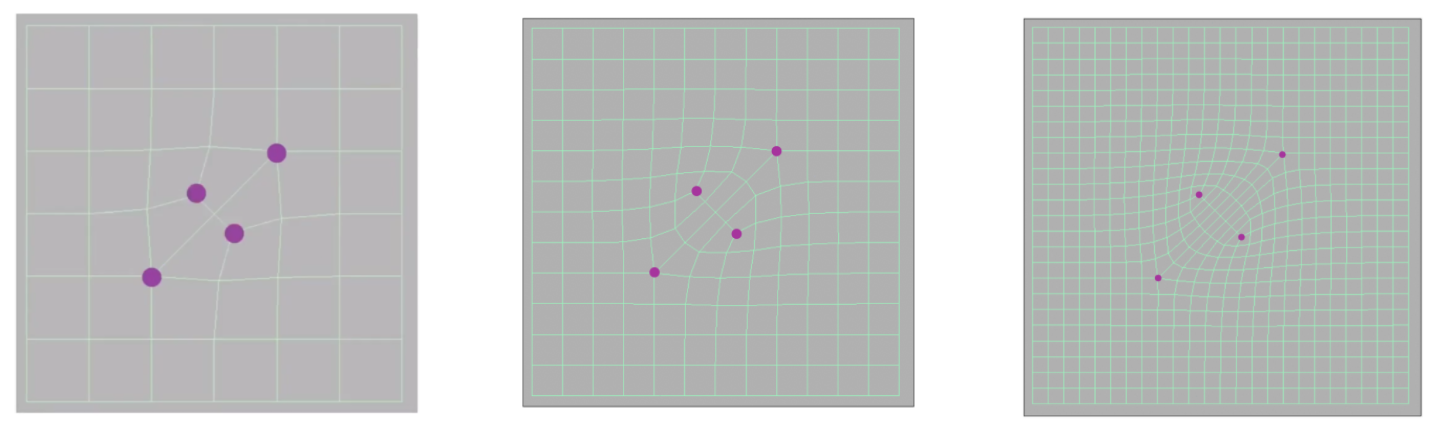
在划分形状的过程中,经过一次划分后:
- extraordinary vertices数量:原始extraordinary vertices数量+原始non-quad faces数量
- non-quad faces数量:无
经过一次划分后,之后extraordinary vertices和non-quad faces数量不再变化。
调整位置
将顶点分为三种类型:
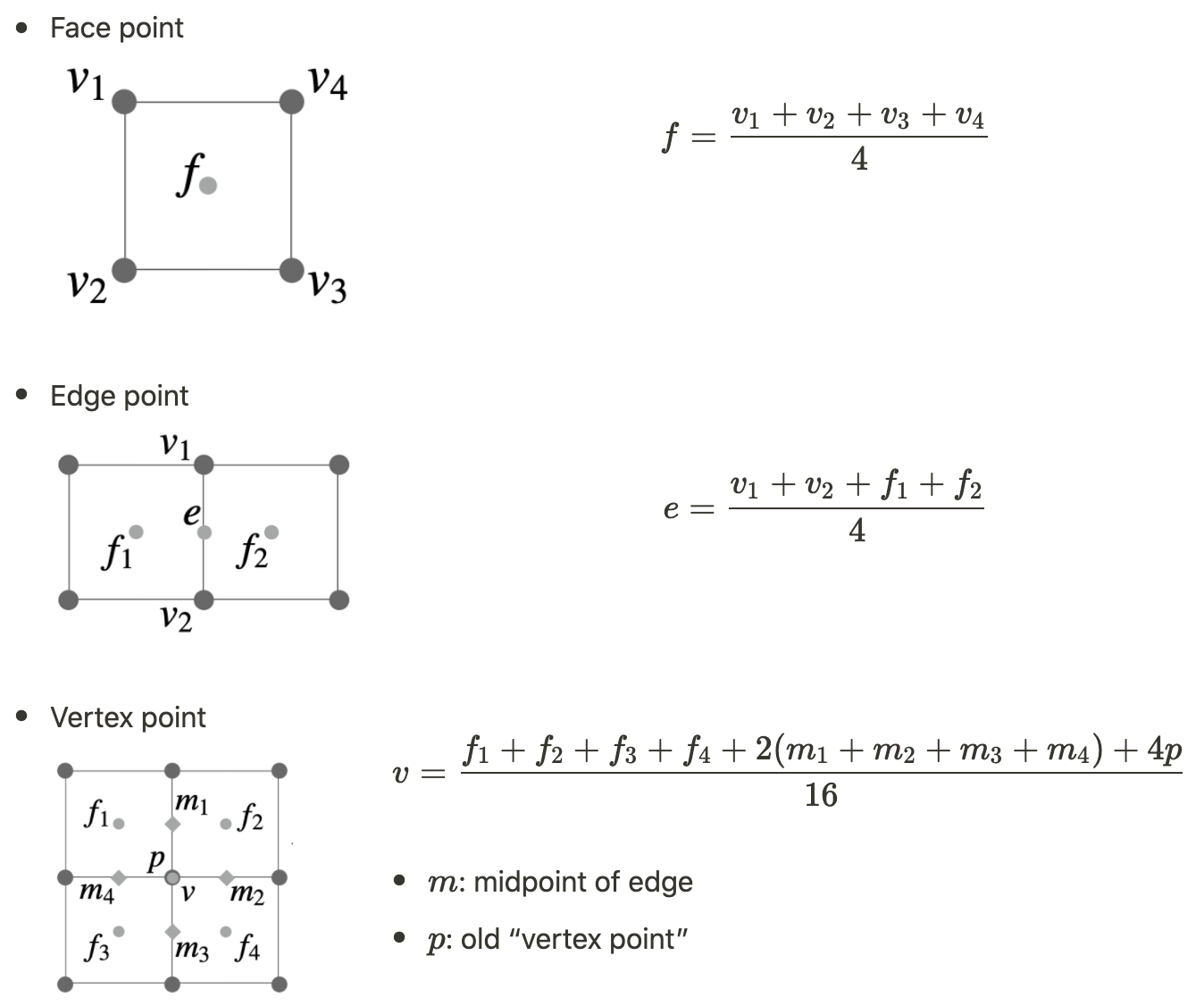
Mesh simplification
目标
reduce number of mesh elements while maintaining the overall shape.

不同的场景下,选择的三角形的数量也不同,主要是考虑性能、存储空间,或者不需要考虑细节。
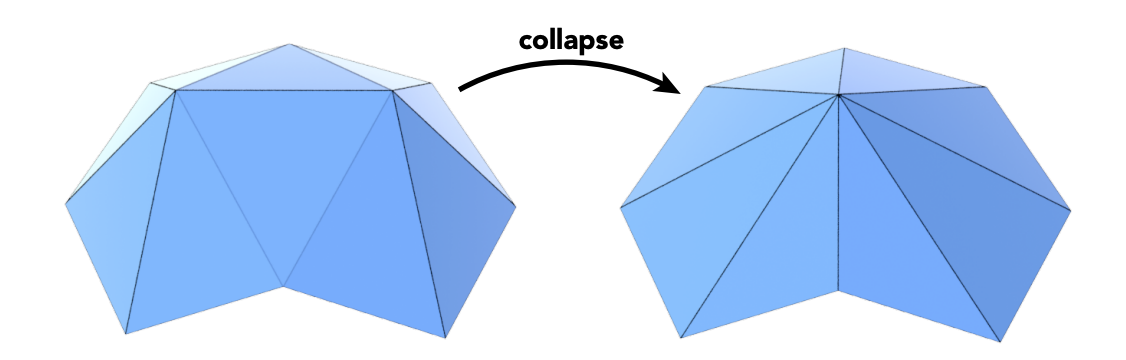
一种方法:Collapsing An Edge
含义
simplify a mesh using edge collapsing
即将一条边转换为一个顶点。
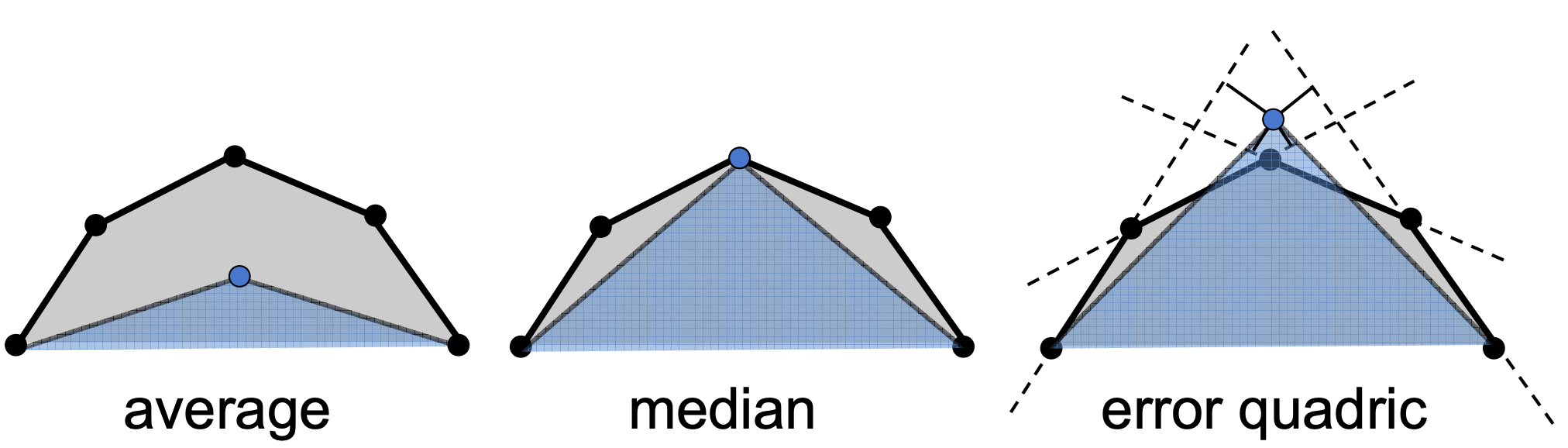
Collapse哪条边—Quadric Error Metrics
在确定通过坍缩一条边来简化图形后,一个问题是:应该坍缩哪条边,能够保持原来的几何形状?或许这个问题换种说法:坍缩后的边形成的节点应该在什么位置,使得能够保持几何形状?变为这个问题后,就不用判断哪条边重要,只要能够保持原有形状,确定新节点的位置即可。
如何确定新节点的位置呢?
- 取相邻点的平均值;
- 取坍缩点的平均值;
- ……
Quadric Error Metrics(⼆次误差度量)用一种度量的方法解决这个问题,该方法问一个问题:
How much geometric error is introduced by simplification?
其思想在于:
Quadric error: new vertex should minimize its sum of square distance (L2 distance) to previously related triangle planes!
因为 Quadric Error Metrics 能够确定新的顶点位置,因此确定坍缩哪条边,可以转换为:坍缩 Quadric Error Metrics 最小的边,这样保证能够保持原有的形状,然后再一次坍缩第二小的,等等。
那么如何坍缩几何图形呢?一种方式是对整个几何图形的所有边都进行坍缩,然后计算每次坍缩操作对应的Quadric Error,然后排序,取最小误差对应的边进行坍缩。
一个问题:当坍缩一条边后,其连接的边也发生了变化,之前对应该边的Quadric Error也就发生了变化。即Quadric Error随坍缩过程会发生动态变化。
因此,上述的做法是行不通的。
实际的做法是:
- 首先对整个几何物体的每条边进行坍缩,取最小Quadric Error对应的边;
- 将与该边连接的其他边对应的Quadric Error更新,再计算剩余最小Quadric Error对应的边;
- 对上述过程不断重复;
该过程需要应用有优先队列或者堆来实现。
一个问题:按照上述过程的顺序得到的所有边,对应的Quadric Error也是从最小到最大吗?显然不一定,其只是局部最小,因此是通过用局部最小代替全局最小——greedy algorithm。但是在实际中,这种方法的效果得到了认可。
效果