光线追踪和光珊化是两个不同的成像方法。
为什么用Ray Tracing
- 在rasterization中一些事情不能很好的处理:
- 不能很好地处理global effect
- 如上一节中提到的shadow mapping, 只能实现hard shadow;
- glossy reflection 光滑的反射;
- indirect illumination 间接光照

- 光栅化很快,但是质量相对较低;
- 不能很好地处理global effect
- Ray tracing 很准确,但是非常慢 光栅化可以realtime,而ray tracing一般是offline。 一般下,在实际场景中渲染一帧需要10k CPU core hours.
基本Ray Tracing算法
Light Rays定义
在图形学中一些假设:
- 光线直线传播;
- 两个光线相遇时,不会发生碰撞;
- reciprocity: 光线是可逆的, 实际是从光源经过各种反射到眼睛,但是我们可以认为是从眼睛发出回溯到光源;
首先——Ray Casting 光线投射
光线投射从眼睛开始,望向物体,假设在眼睛面前存在一个屏幕,里边被分为各种像素点。
- 将眼睛和物体连接起来的光线与屏幕相交的地方形成一个点,多个点形成一个image;
- 并将投射到物体上的光线回溯到光源,以确定光源能看见物体上的该点,从而验证有无投影;
💡 在光线追踪中,使用的是Pinhole camera model,即眼睛视为点光源。
第一步:generate eye rays
从眼睛开始,望向物体,得到最近的物体上的点。一条eye ray可以与很多点相交,但是这一步只取最近的点,相当于做了深度测试。
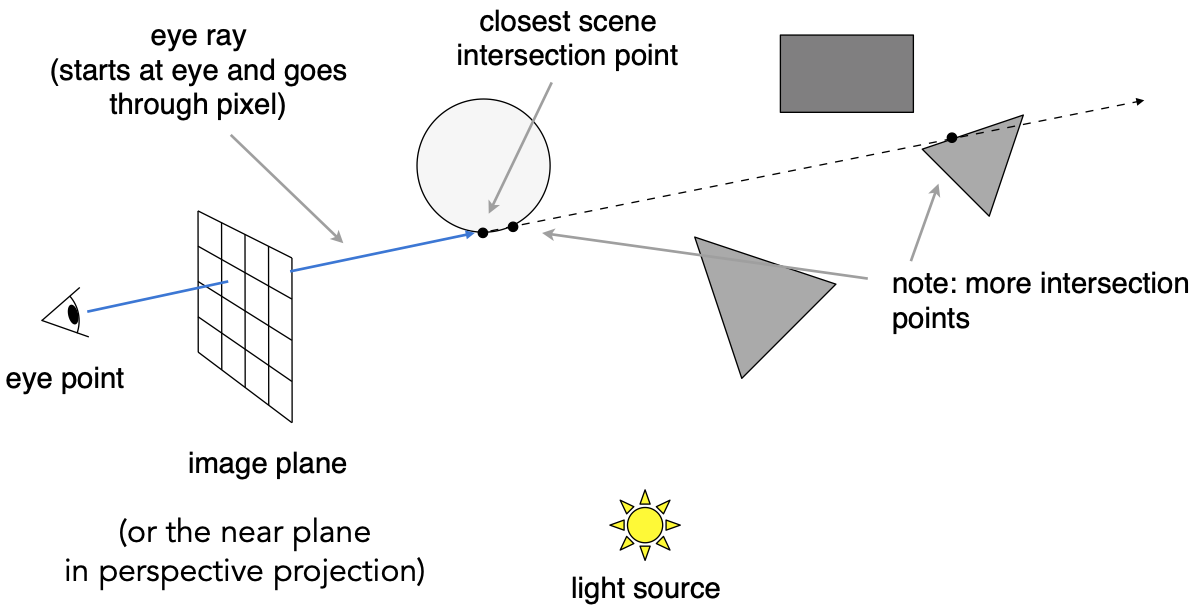
第二步:Shading pixels
将获得的距离屏幕最近的点与光源相连,确定该点是否可见。然后对于该最近的点而言,其得到了两条线,从而可以确定法线,以便利用着色模型(Blinn Phong Model等)完成颜色的计算,然后写会到屏幕对应的像素上。
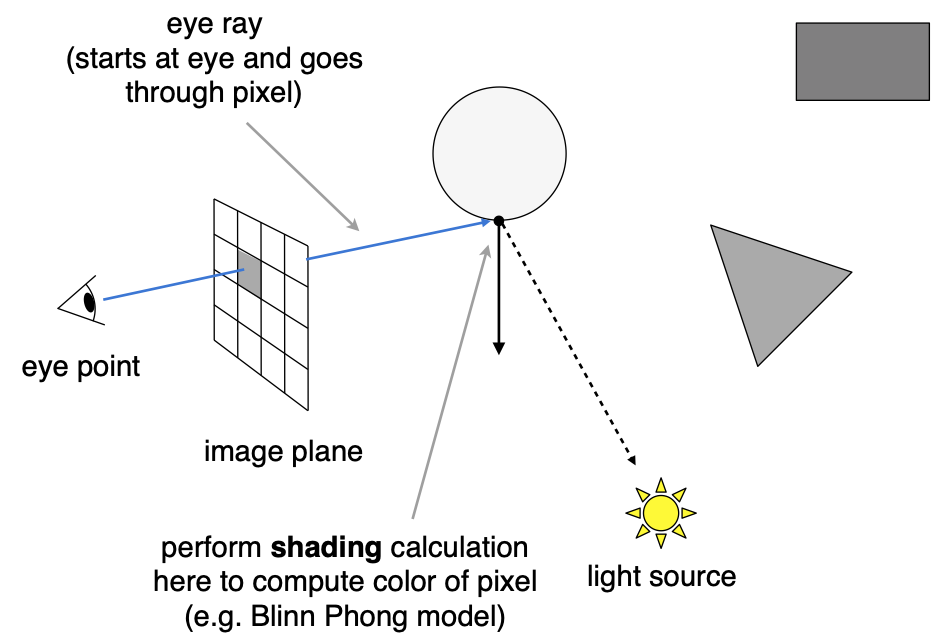
上述简单的光线追踪:
- 基本可以达到光栅化一样的效果;
- 但是光线只能bounce一次;
Recursive(Whitted-Style) Ray Tracing
为了解决上述模型中光线只能弹射一次的问题。
原理
当eye ray射出来后,照到一个玻璃球上,会出现反射和折射,在一个点上可以无限地bounce。
在这种情况下,计算着色值的方式与上述模型不同。在上边只会计算一个最近点与光源相交后得到的着色值,现在需要计算所有的点与光源相连后的着色值,因此whitted-style下,需要将每个弹射点计算得到的着色只加到一起写到对应的像素上(除了阴影下的点)。
对每一个弹射点都需要首先确定是否能被光源看见,来确定是否包含其贡献的着色值。
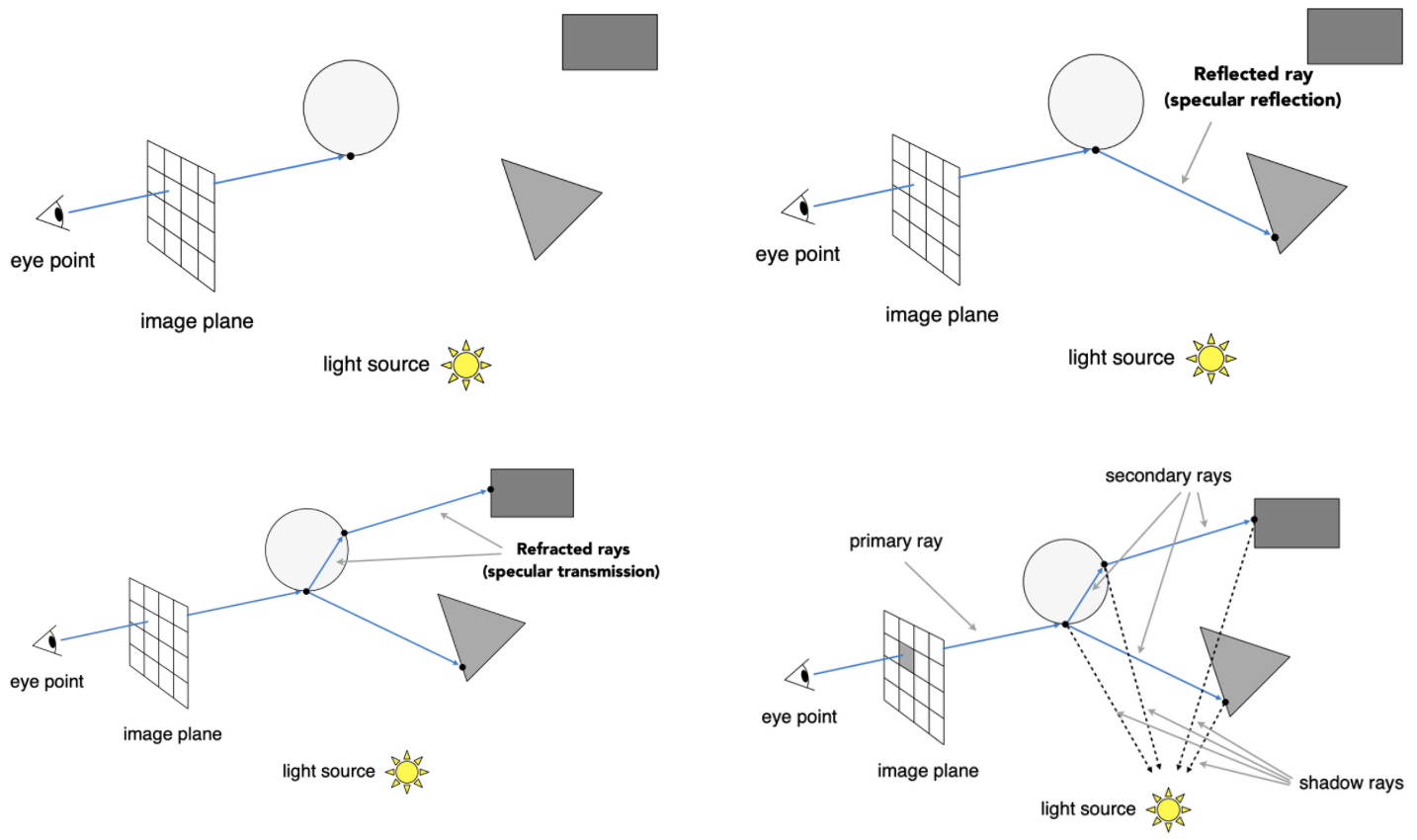
几个定义:
- primary ray: 与第1个弹射点对应的ray
- secondary ray: 除了第1个弹射点对应的其他ray
- shadow ray: 与光源连接的ray;
Ray-Surface Intersection
Ray equation
光线在数学上的定义如下,
Ray is defined by its origin and a direction vector.
- 光线起点 $\mathbf{o}$;
- 沿着方向的单位向量;
$$
\mathbf{r}(t) = \mathbf{o} + t\mathbf{d}; \quad 0 \le t \le \infty
$$
- 其中,$t$为时间;
Ray Intersection With Sphere
对于球的表达:
- 定义球心 $\mathbf{c}$;
- 球上任意一点 $\mathbf{p}$;
则对于球面上的任意一点表示如下,
$$
(\mathbf{p} - \mathbf{c})^2 - R^2 = 0
$$
当求解光线与球体的交点时,需要满足:
$$
(\mathbf{o} + t\mathbf{d} - \mathbf{c})^2 - R^2 = 0
$$
求解t即可,二次函数求解,要保证t为正实数。根据解的数量的不同可以有3种情况:
- 相离:无解;
- 相切:一个解
- 相交:两个解
Ray Intersection With Implicit Surface
将情况推广到任意的隐式平面,对于任意平面,根据之前的几何部分的知识,表示如下:
$$
f(\mathbf{p}) = 0
$$
因为为了求解交点,得到如下表示:
$$
f(\mathbf{o} + t\mathbf{d}) = 0
$$
下一步就是利用各种数值计算的方法和软件完成计算即可。
Ray Intersection With Triangle Mesh(显式表示)
简单的方法
- 将光线与每个三角形分别计算,带来的问题必然很慢。
- 这里我们,我们只考虑光线和三角形有0或者1个交点的情况,不涉及平行的情况。
对于一个mesh,我们首先考虑针对一个三角形的交点求解,然后迭代即可。
将光线与三角形求交分解为2部分:
- ray-plane intersection;
- test if hit point is inside triangle;
根据高数中平面方程,可以通过平面的法线和面上的一点来确定平面本身。
Plane is defined by normal vector and a point on plane.
对于平面上的任意一点 $\mathbf{p}$,给定法线 \mathbf{N}和给定一点 $\mathbf{p}^{\prime}$,得到以下表示:
$$
(\mathbf{p} - \mathbf{p}^{\prime}) \cdot \mathbf{N} = 0
$$
得到表示,就可以求解交点了,满足如下条件:
$$
(\mathbf{p} - \mathbf{p}^{\prime}) \cdot \mathbf{N} = (\mathbf{o} + t\mathbf{d} - \mathbf{p}^{\prime})\cdot \mathbf{N} = 0
$$
得到:
$$
t = \frac{(\mathbf{p}^{\prime} - \mathbf{o}) \cdot \mathbf{N} }{\mathbf{d} \cdot \mathbf{N}}
$$
最后别忘了一步,判断t对应的交点是不是在三角形内部。
Möller Trumbore Algorithm
上面的方法所有简单,容易理解,但是过于繁琐。
有一种快速的方法,可以一下得到答案。
📌 一种思考方式:三角形内部一点可以使用重心坐标表示,因此判定光线与三角形相交,就可以将其表示为重心坐标的形式。
$$
\mathbf{o} + t\mathbf{d} = (1- b_1-b_2) \mathbf{p}_0 + b_1\mathbf{p}_1 + b_2\mathbf{p}_2
$$
这个方程本质上是求解线性方程组,使用Cramer’s rule完成求解(还记得这是当初学线性代数时第一个主要内容)。
完成求解后需要验证:
- t为正实数
- $b_1, b_2, 1-b_1 - b_2$ 为正实数,保证在三角形内部;

