Cache内部的逻辑结构
回顾之前的内容,为了确定cache中是否有数据以及如何找到这些数据,在cache中已有存在:
- valid bit:判断cache line中是否有来自内存的数据;
- tag 字段:标识main memory的高位地址;
- index:标识cache line的序号;
从硬件上来说cache主要是SRAM和控制逻辑电路组成,但是其内部的逻辑结构可以看成是上述3者,加上数据字段,构成一个cache line,如下所示。

- 在该图中,cache共有16个cache lines;
- 数据段中对应一个block,也是main memory中访问得到数据的最小单位(利用了空间局部性原理),这里一个block是16个字节;
读数据的简要过程
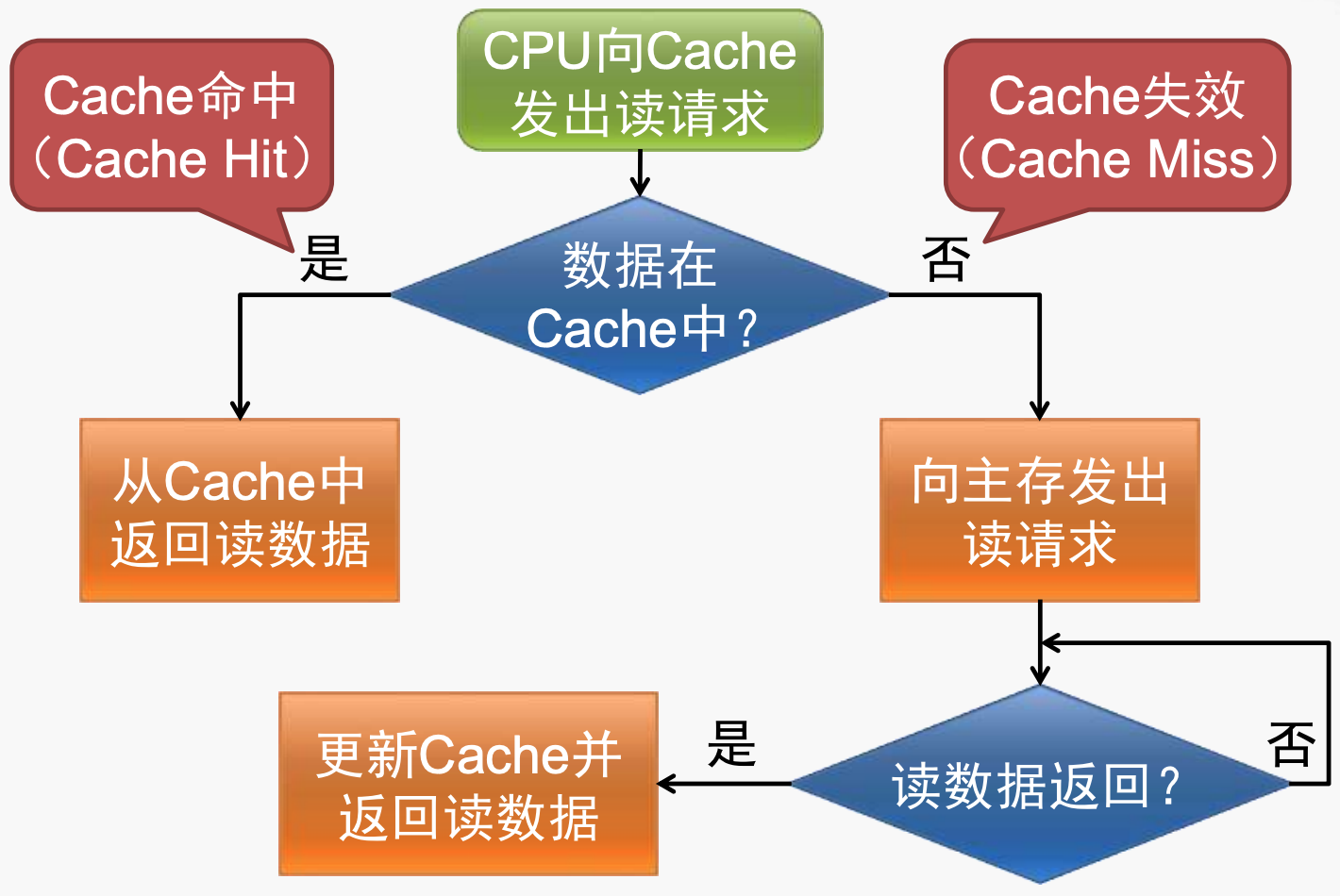
Cache的简单访问过程如上图所示:
- 当数据在cache中,这种情况称为hit,数据直接从cache中返回,这种是最理想的情况,也是最能发挥cache作用的场景;
- 当访问的数据不在cache中时,称为miss,此时需要向main memory发起读请求,当得到数据后,注意,此时得到的数据不仅仅是访问的数据,而是包含访问数据的一个连续的序列,之后将cache中的数据更新,并返回读取的数据;
几个概念
hit rate(hit ratio): The fraction of memory accesses found in the upper level of the memory hierarchy.- 这个概念一般用在cache上;
- 但是这里定义的很general,例如,理论上,main memory 对于disks也可以看作“cache”, 因此对于main memory也可以计算 hit rate;
miss rate:1 - hit rate, the fraction of memory accesses not found in the upper level.
由于访问速度是memory hierarchy提出的核心诉求之一,因此基于上述两个概念,有几个相关的概念:
Hit timeis the time to access the upper level of the memory hierarchy.- including the time needed to determine whether the access is a hit or a miss. 即这部分时间也包括比较tag标签和valid bit的时间;
miss penaltyis the time required to fetch a block into a level of the memory hierarchy from the lower level, including:- the time to access the block,
- transmit it from one level to the other,
- insert it in the level that experienced the miss,
- and then pass the block to the requestor.
相比于miss penalty,hit time很小,因此优化访问性能的主要关注点一般在减小miss penalty。
读数据过程的具体分析
举例说明
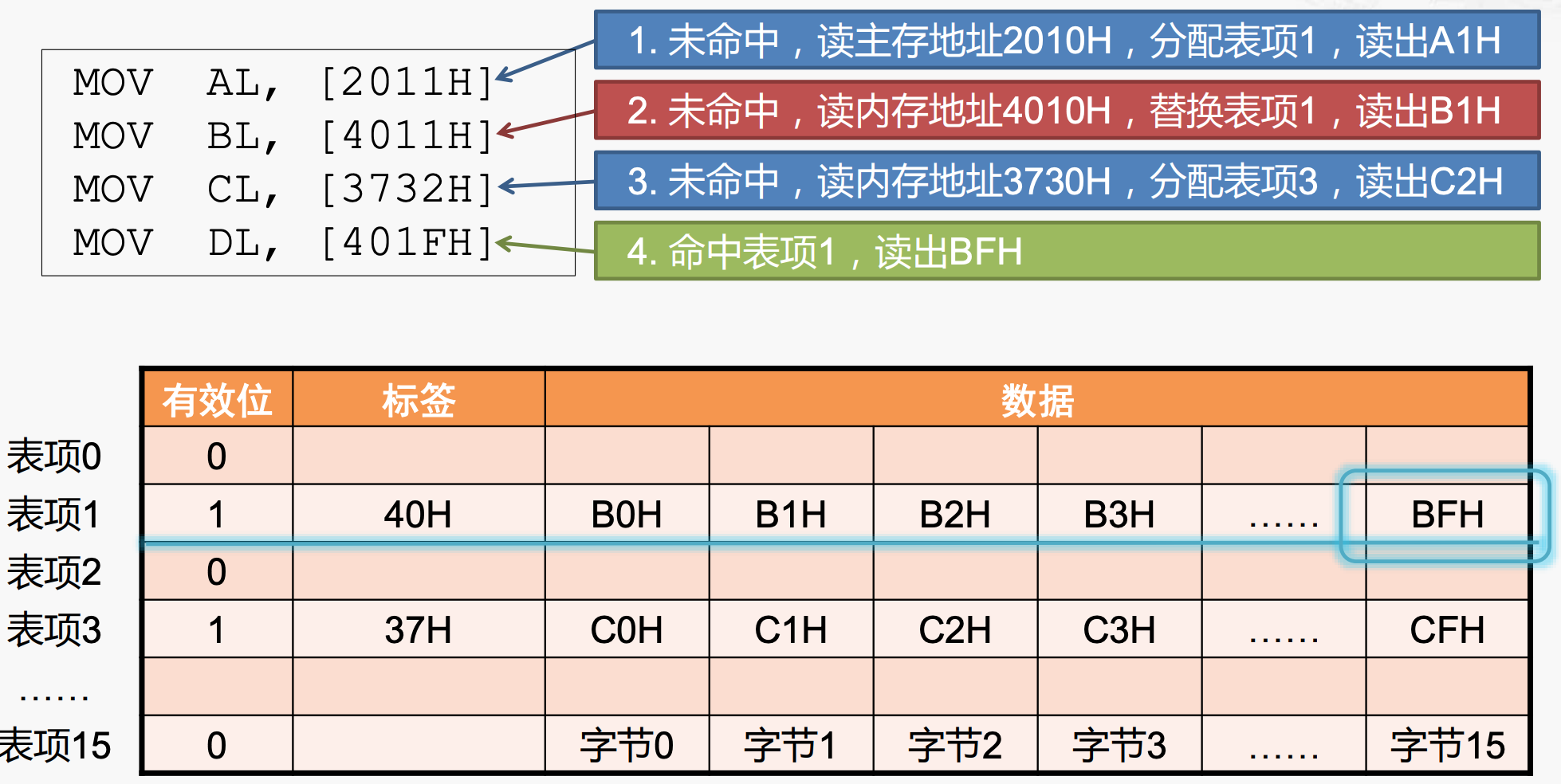
当CPU执行如下的汇编代码时,发生了什么?
MOV AL, [2011H]
MOV BL, [4011H]
MOV CL, [3732H]
MOV DL, [401FH]
- 首先要确定汇编指令,这些指令均是将内存地址中的数据移到通用寄存器中;
- 确定访问的main memory的地址:
MOV AL, [2011H]会直接访问2011H对应的内存地址吗?答案是不会的,因为,cache line在上图中,每个block为16个字节。为了利用空间局部性原理,cache一次要读取一个block——16个字节,因此需要16个字节对齐。因此虽然是将2011H地址上的数据移到AL寄存器上,但是cache发出的地址是2010H(这是16个字节对齐后的地址)。
如何判断地址是否对齐,可以参考Stack Overflow中的一个回答。顺便想到,在x86中,word是2个字节对齐的,MIPS中是4个字节对齐的。
根据读操作的具体过程,可以分为以下几种情况。
miss:分配cache line
在这种情况下,将[2011H]地址变为[2010H]地址,这里怎么理解?2011H地址是一个16进制的数,其中共有16位,也就是内存16位对齐。
转换为10进制的过程与2进制相同:
$$
2 \times 16^3 + 0 \times 16^2 + 1 \times 16^1 + 1 \times 16^0
$$
要保证16bit对齐,最后一位必须是0,所以这就是[2011H]到[2020H]内存地址转换的具体含义。
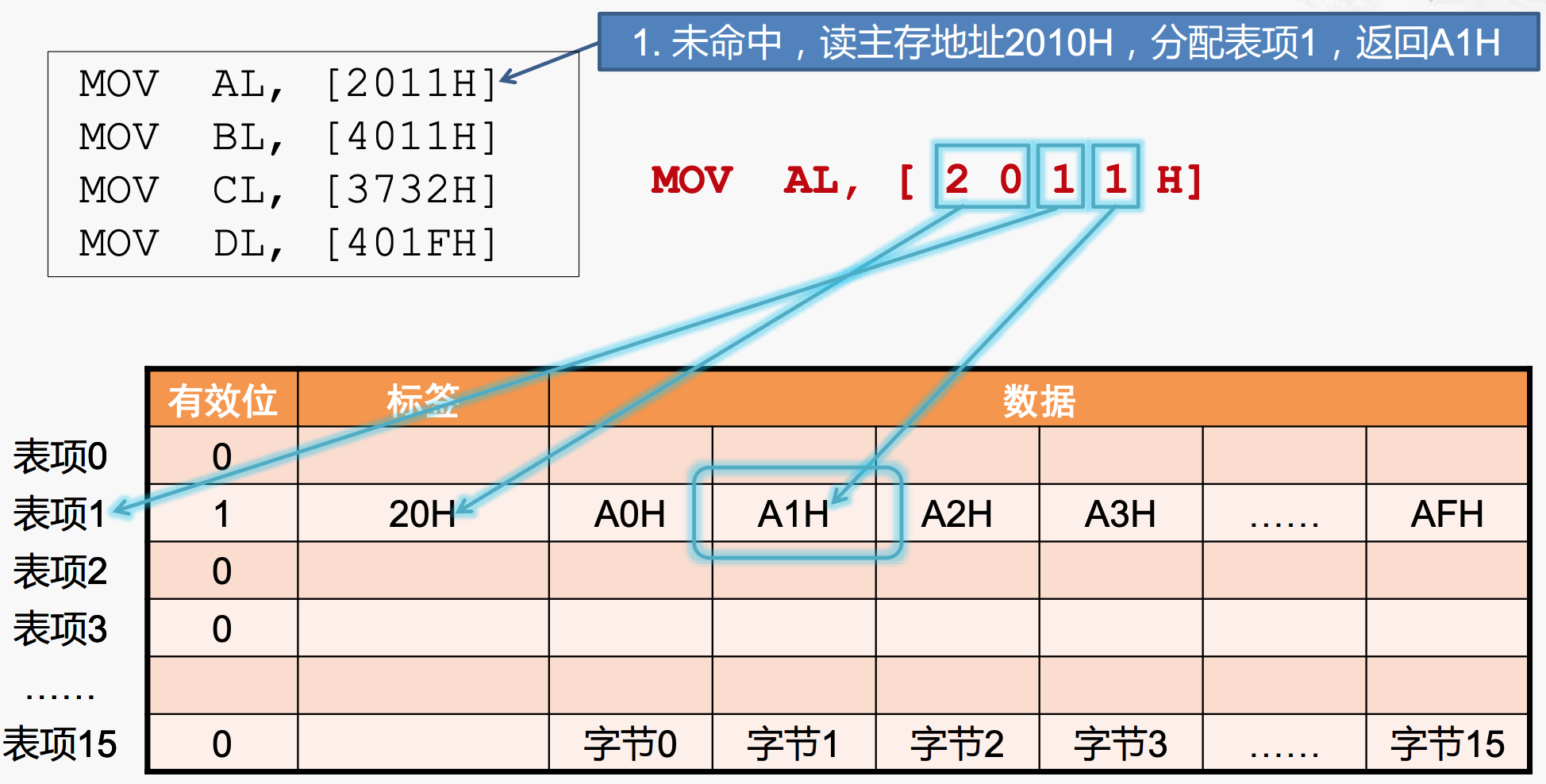
cache访问内存的[2010H]地址获取数据,一共得到16bit的数据,就放在cache line的数据单元中,具体的放置规则如下:
- 选取哪个cache line?根据倒数第二位,这是一个16进制的数,通过对16取余,正好是该位上对应的数字,恰好可以对应16个cache lines;
- 得到对应的cache line后,将数据放入其中,如何获取真实地址[2011H]对应的数据,看最后一位,是当前表项从开始的偏移量位置对应的数据,也就是A1H,返回给CPU即可;
- 填充tag:将除了末尾两位之外的其他地址数据放到标签中;
- 置valid bit为1;
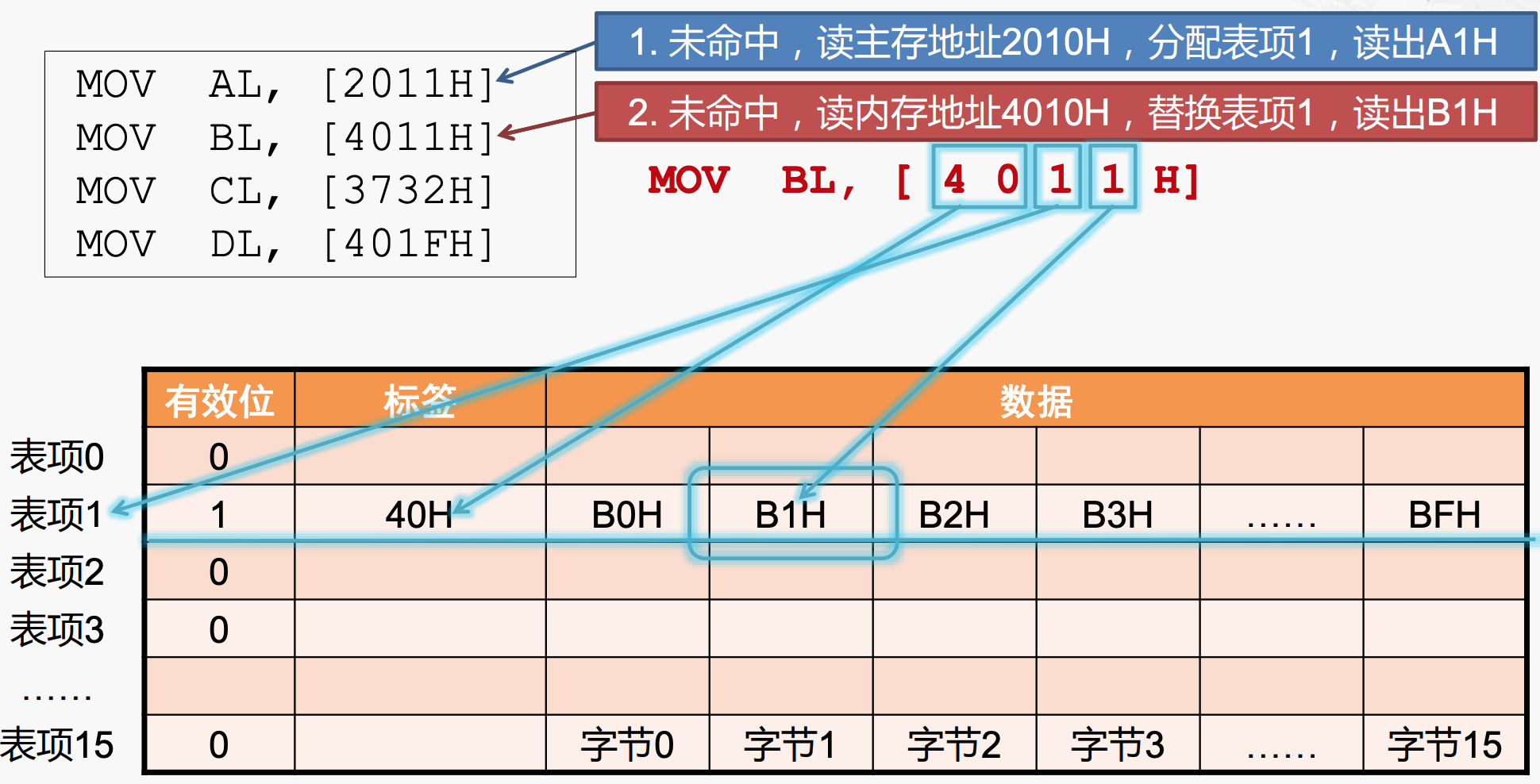
miss:替换cache line
当执行MOV BL, [4011H]指令时,发现这个内存地址对应的cache line也是1,但是发现tag部分不同,因此对应不同的内存地址,发生miss,需要去main memory重新读取数据,填充到cache line 1中,新的数据来临,与cache line 1中的数据发生冲突,将其替换即可。
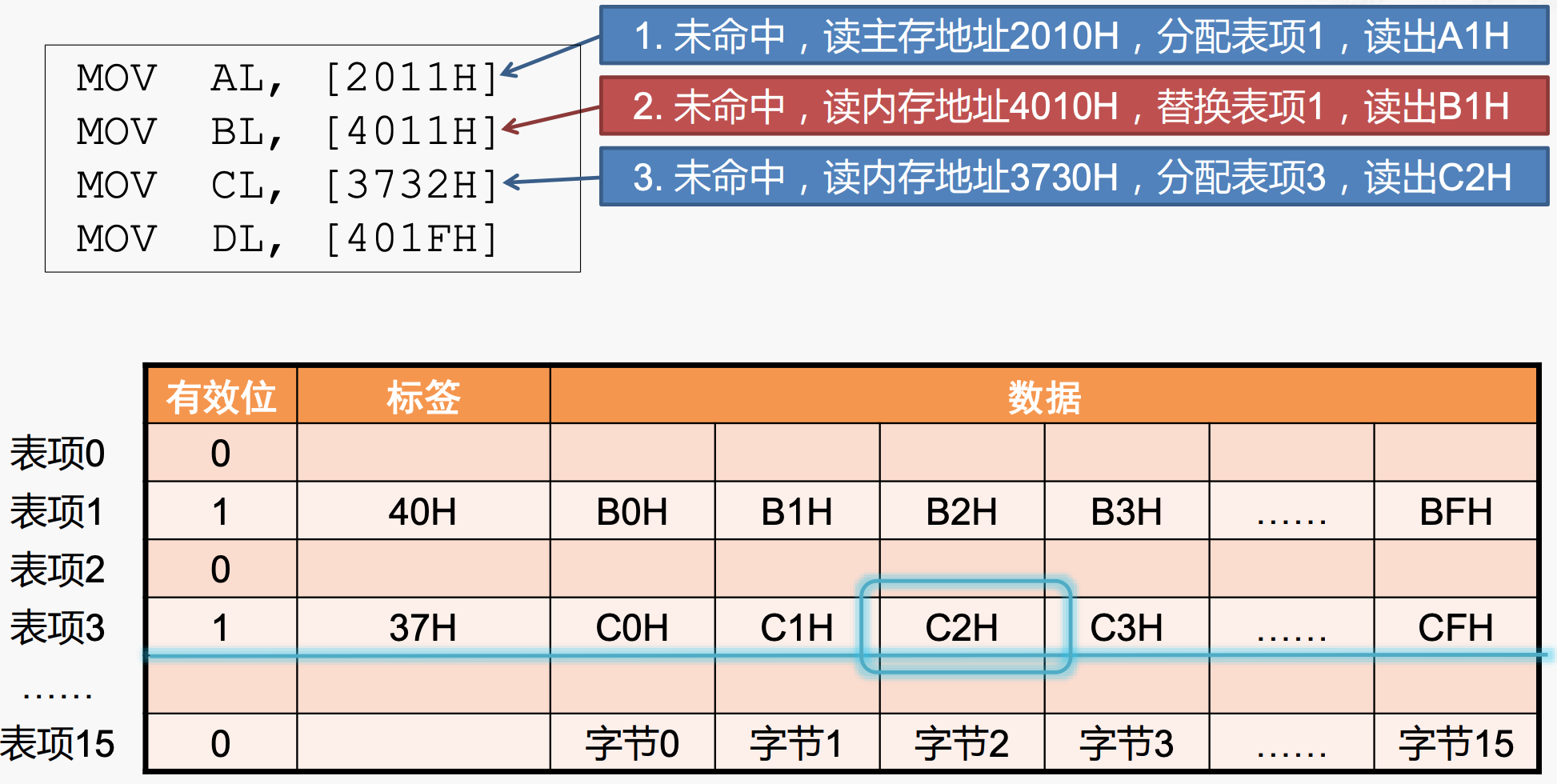
miss:分配新cache line
当同样发生miss时,但是数据访问的内存地址在cache line 的tag中没有出现过,因此没有冲突,直接访问main memory继续访问数据即可。
hit:读取cache line
最好的情况是命中,按照之前写入的规则读取对应的数据返回。访问内存地址[401FH]对应的数据时,发现在cache line 1中出现index 和tag同时匹配,因为内存地址为concat(tag, index),然后读取[4010H]对应的数据,再加上偏移量,得到BFH。
澄清:内存与cache的地址对应关系
前面我们说到当CPU发出访问数据的请求时,直接给出的是内存地址,这些内存地址可以通过拆分对应到cache的位置上,如下:
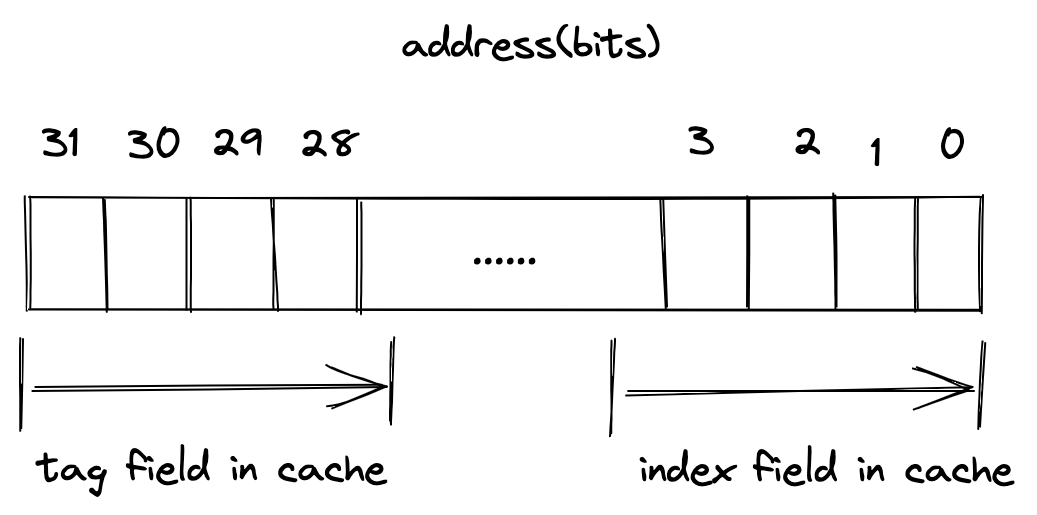
但是,因为有内存地址对齐机制的存在,上述的地址转换并不完全准确。在MIPS中,当lh读半个word(MIPS中一个word为4个字节),存储器的地址必须是2的整数倍(地址结尾必须有1个0); lw 读一个word时,存储器的地址必须是4的整数倍(地址结尾必须有2个0)。
我们以MIPS访问一个word为例进行说明,因为它也是以一个word,4个bytes实现地址对齐的。对于32位地址的情况,内存地址如下:
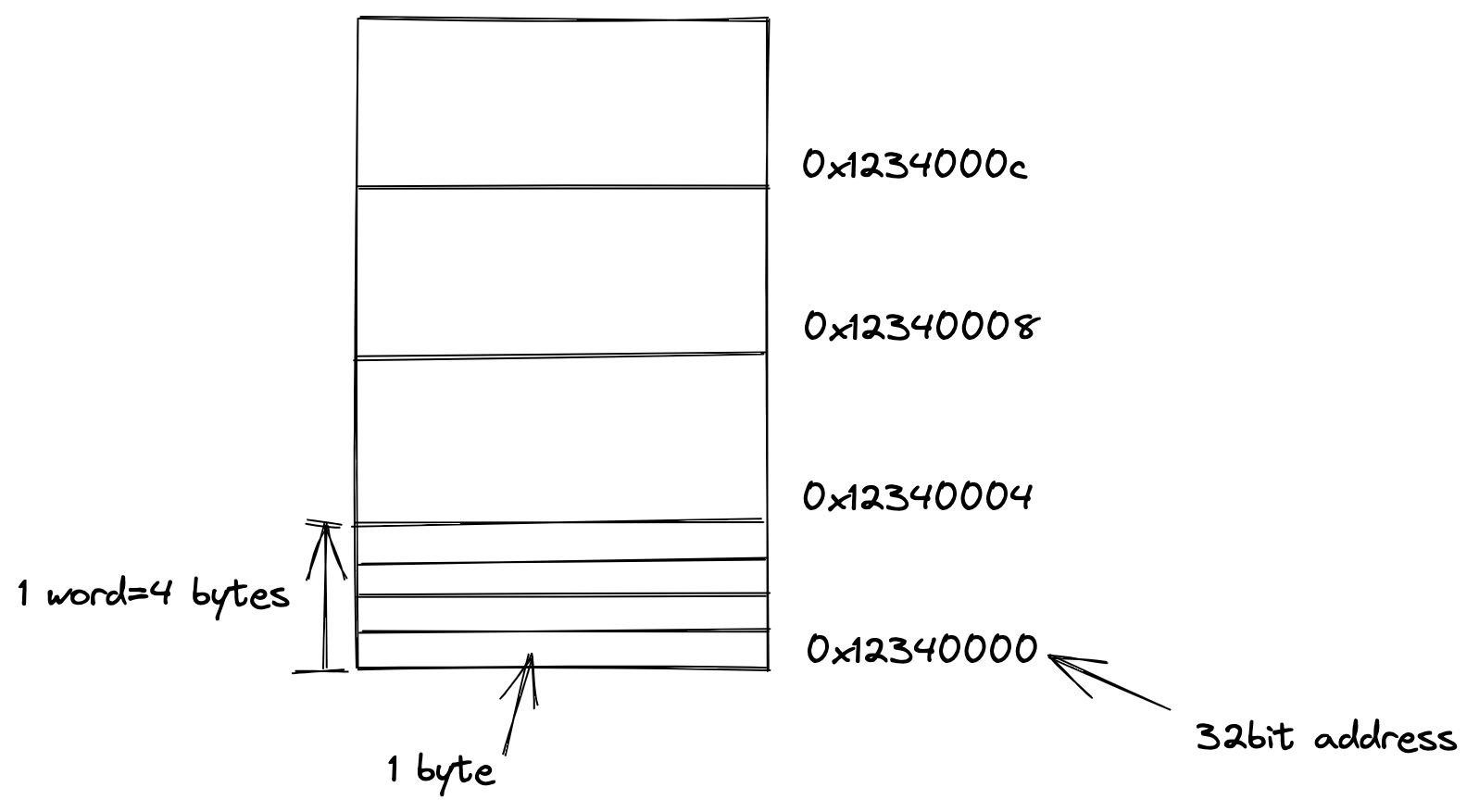
在前面提到过,为了更好地利用空间局部性原理,cache从main memory中读取数据时,一般按照以block为单位进行读取,一个block填入cache line中,而block中一般有若干个words。
基于这种情况,如何将main memory的地址对应到cache中呢?应该是分为以下几个步骤:
- 确定index字段,确定具体的cache line;
- 确定cache line的tag字段,是否一致; 到此为止已经确定了一个cache line中block;
- 之后,需要确定是block中第几个word;
- 更进一步,因为一个word是4个字节,如果要访问一个字节的数据,还需要确定偏移量,这个偏移量一般是固定的,与对齐的方式有关,例如MIPS中是4个字节对齐,x86是2个字节对齐;
到此为止,算是比较完整的main memory地址映射到cache上。
cache line中的block大小可以变化,扩大容量或者缩小容量,但是这种操作会影响其他字段,比如index或者tag字段。如下举几个例子:
例1:tag=10,index=10
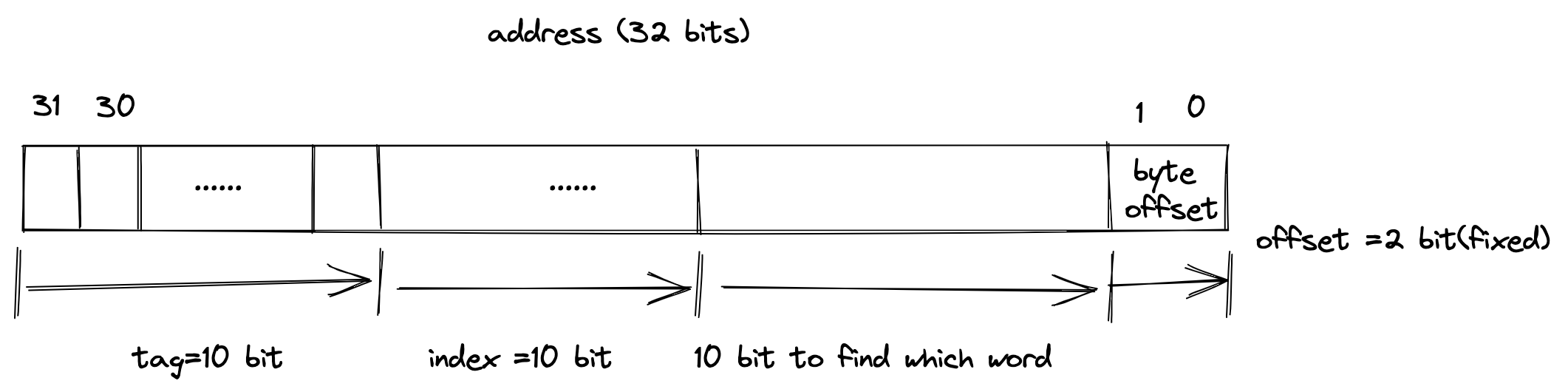
这种情况下,32位地址中用于决定选择哪个word的bit只有10个,即能寻址 $2^{10}$ 个words,每个word都可以通过byte offset在一个word内部确定选择哪个byte,来应对MIPS中lh等指令。
例2:tag=10,index=5
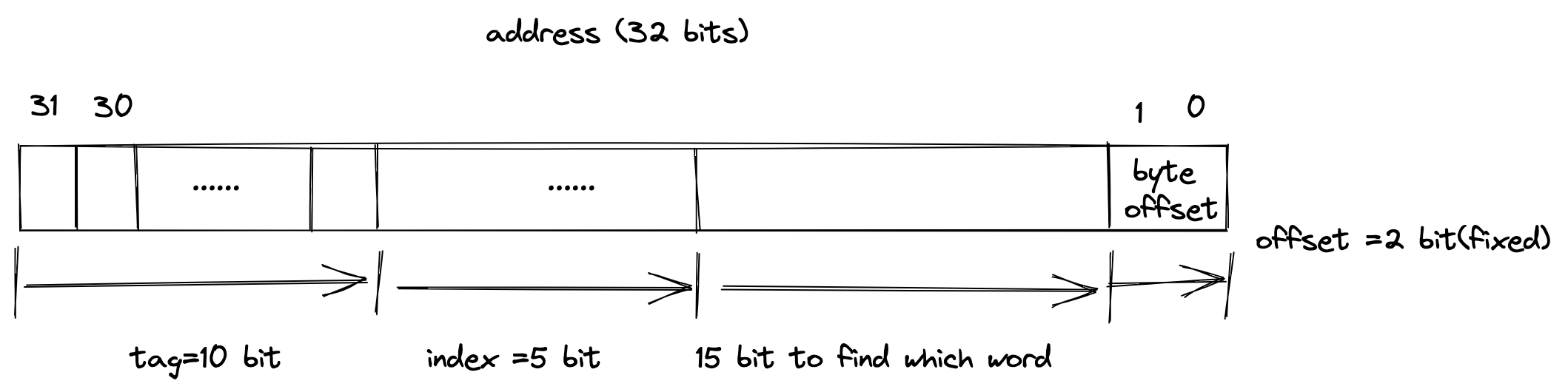
这种情况下,32位地址中用于决定选择哪个word的bit有15个,即能寻址 $2^{15}$ 个words,但是此时index数量减少,因此这种情景下,cache line内部的block容量增加了,但是整体的cache lines数量减少了。
减少miss——扩充cache capacity?
如何计算cache capacity
计算cache的容量,需要了解如何将main memory的地址放到cache中。
举例说明,如下场景中:
- 32位地址;
- direct-mapped cache structure
- cache中共有 $2^n$ 个lines,也说明每个cache line中的index字段共有n个bits;
- 每个cache line中有一个block,每个block能存储 $2^m$ 个words,说明用于寻址words的地址中的位数有m位。
根据这些信息,我们可以计算tag字段有几个bits:
$$
32 - ( n + m + 2)
$$
- n为index 的bits;
- m为寻址words的bits;
- 2是byte offset的bits,MIPS中固定为2个bits;
在一个direct-mapped cache中所有的bits如下:
$$
2^n \times (\text{block size} + \text{tag size} + \text{valid field size})
$$
- block size $$
2^m \times 32
$$
因此,所有的bits为:
$$
2^n \times (2^m \times 32 + (32 - n - m - 2) + 1)
$$
这个计算结果是cache中所有的bits,但是一般我们只考虑用于存储数据的bits,即:
$$
2^n \times 2^m \times 32
$$
根据这个计算公式,可以知道上述的例1和例2中的容量(只有数据的)分别为:
$$
2^{10} \times 2^{10} \times 32
$$
$$
2^5 \times 2^{15} \times 32
$$
均为4MiB的cache。
分析cache capacity的影响
在读数据的具体过程中,发生miss的情况,非常影响访问性能,那么从硬件的角度来看,增加cache的容量,使得main memory中的多数尽可能的驻存在cache中,理论上可以降低miss rate,也是空间局部性的体现。
但是,情况并不是我们理想的那样。当cache line中的block size增加后,会发生什么?
一个cache line中存储的words数量增加,但是从上述的例1和例2中可以看出,block size增加(即用于寻址的bits增加),对应的cache lines的数量或者tag的位数就会减少,这导致了对于cache lines的争夺激烈,会发生当一个main memory的数据进入cache后,还未来得及被hit,就已经被新进来的main memory的数据替换,大量发生冲突。
另外一个是,当block size增加后,miss时引入的性能下降也会增加。即,当发生miss时,需要cache从main memory中读取数据,这个过程在上面提到共2个部分:
- 对于block数据中第一个word的定位时间延迟;
- 将所有的数据传输到cache;
因为block size增加,导致传输时间大幅增加,因此miss penalty大幅增加,因此可能会导致block size带来的性能的提升抵不上miss penalty带来的性能下降。
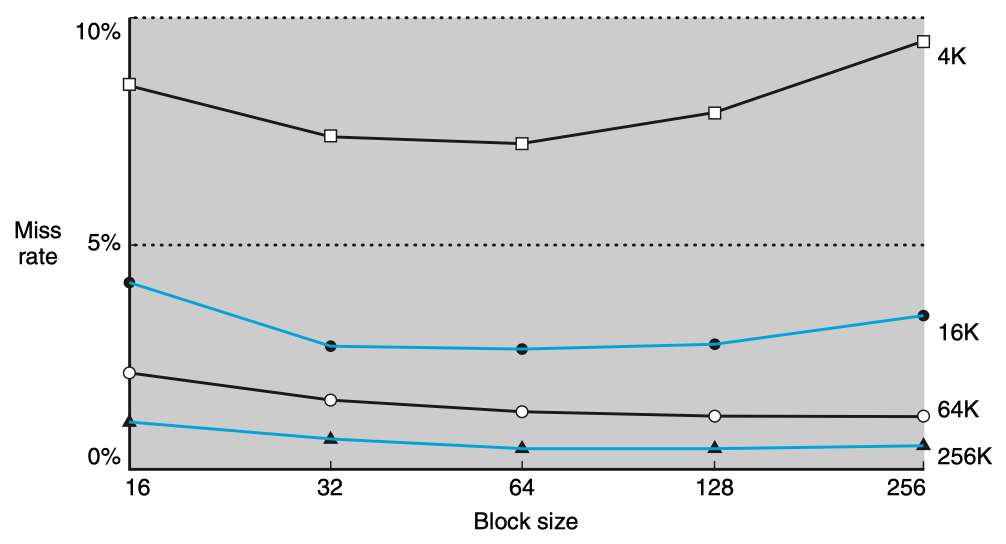
从上图看出:
- 同样cache size,随着block size的增加,其miss rate先下降之后上升,就是因为上述的原因;
- 而cache size的增加,增加的可以是cache lines的数量,这样可以减少冲突,从而减少miss rate.
参考资料
Computer Organization and Design : the hardware/software interface

